题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

解题思路：

对于给定的两个字符串S和T。

如果S和T的长度不相等，T肯定不是S的扰乱字符串。

如果S和T的长度相等，则可以在某一个随机下标处进行分割，会将两个字符串S分割成两部分，同理，T也可以用两部分表示，如下如所示：

字符串S被分割为S1和S2，字符串T被分割为T1和T2，此时可以分为两种情况：

1. 情况一：S1和S2没有交换，此时需要判断T1是否是S1的扰乱字符串，T2是否是S2的扰乱字符串。
2. 情况二：S1和S2交换了，此时需要判断T2是否是S1的扰乱字符串，T1是否是S1的扰乱字符串。

显然上述分割会将大问题分割成两个小问题：

1. T1是否是S1的扰乱字符串，T2是否是S2的扰乱字符串
2. T2是否是S1的扰乱字符串，T1是否是S2的扰乱字符串

子问题的解题问题和大问题的解题步骤类似，显然可以使用动态规划来求解。

1. 定义状态：dp[i][j][m][n]，表示T[m，...，n]是否是S[i，... ，j]的扰乱字符串，因为如果是然乱字符串，那个相同部分的长度一定相等，即 n - m = j - i = len，所以可以将四维数组优化为三维数组，d[i][j][len]，表示字符串T中从j开始的len个字符串是否是从字符串S中 i 开始的len个字符串的扰乱字符串。
2. 状态转移方程：
   1. 假设随机划分处使得S1的长度为k，如下图所示：​​​​​​​
   2. 对于情况一，不交换S1和S2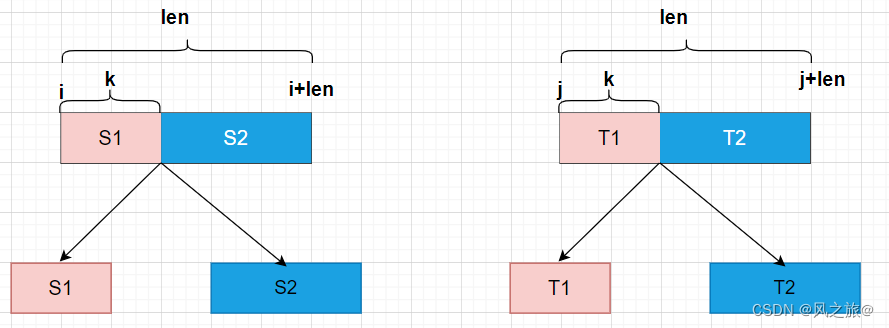：此时需要判断T1是否是S1的扰乱字符串，T2是否是S2的扰乱字符串，所以dp[i][j][len] = dp[i][j][k] && dp[i+k][j+k][len-k]
   3. 对于情况二，交换S1和S2：此时需要判断T2是否是S1的扰乱字符串，T1是否是S1的扰乱字符串，注意：需要令T2和S1的长度相等，T1和S2的长度相等，所以，dp[i][j][len] = dp[i][j+len-k][len] && dp[i+k][j][len-k]
   4. 上述只是判断了一处分割位置的状态转移方程，我们需要枚举出所有的分割位置，所以最终的状态转移方程为：dp[i][j][len] = ( dp[i][j][k] && dp[i+k][j+k][len-k] ) || ( dp[i][j+len-k][len] && dp[i+k][j][len-k] )，其中对于每一个len，k都需要从1枚举到 len-1，只要有一个枚举位置可以令 dp[i][j][len] 等于true即可，此时就可以结束枚举了。
3. 初始状态：两个长度为1的字符串，显然如果这两个字符相等，则 dp[i][j][1] = true，否则false

AC代码：

class Solution {
    public static boolean isScramble(String s, String t) {
        int n = s.length();
        int m = t.length();
        if (n != m) {
            return false;
        }

        boolean[][][] dp = new boolean[n][n][n + 1];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                dp[i][j][1] = s.charAt(i) == t.charAt(j);
            }
        }

        for (int len = 2; len <= n; len++) {
            //枚举s中的位置
            for (int i = 0; i <= n - len; i++) {
                //枚举t中的位置
                for (int j = 0; j <= n - len; j++) {
                    //枚举分割的位置
                    for (int k = 1; k <= len-1; k++) {
                        //不交换S1和S2
                        if(dp[i][j][k]&&dp[i+k][j+k][len-k]){
                            dp[i][j][len]=true;
                            break;
                        }
                        //交换S1和S2
                        if (dp[i][j+len-k][k]&&dp[i+k][j][len-k]){
                            dp[i][j][len]=true;
                            break;
                        }
                    }
                }
            }
        }
        return dp[0][0][n];
    }
}