一、说明

本文是数据专家的体会，他之前写了一系列关于时间序列的文章，在这些文章之后，他想给出一个关于我们如何通过投资组合分析在潜在风险情况下将自己保持在安全区域的想法。文章专业性很强，但机器学习方面的工作还是有参考价值的。

可参考访问以前的文章，可以使用以下链接：

时间序列简介
时间序列中的计量经济学和统计模型
使用 LSTM 进行时间序列预测
Python中的投资组合分析：乌克兰战争对欧美公司的影响

二、那么这个波动性是什么？

波动性是金融市场的核心。它扮演着双重角色——既是投资者的信息灯塔，也是众多金融模型中的关键组成部分。但为什么波动性会引起如此多的关注？答案植根于一个词：不确定性。这种不可预测性因素是金融模型机制的基础。

随着金融市场的全球一体化，我们看到不确定性的放大，凸显了波动性的作用。该术语描述了金融资产价值波动的强度，通常作为风险的象征。可以毫不夸张地说，波动性在资产定价和风险管理等领域占据了中心位置。

现在，如果您以前深入研究过金融世界，您可能会遇到“波动性聚类”或“信息不对称”等术语。从历史上看，我们一直依靠ARCH和GARCH等传统模型来预测波动性。然而，他们并非没有缺陷。鉴于最近的市场动荡和机器学习取得的进步，人们对改进预测波动性的方式重新产生了兴趣。

三、使用 Python 对波动性进行建模

本文将深入探讨用于波动性预测的传统和当代模型（想想SVM）。为了有效地对波动性进行建模，必须识别模型中的组成部分或“特征”。这本质上意味着对不确定性本身进行建模，以便为现实世界的预测提供更清晰的视角。

那么，我们如何衡量这些模型的有效性呢？输入由以下公式定义的“回报波动率”或“实际波动率”：

实际波动率

哪里：

“r”代表返回
“mean（r）”代表平均回报
“n”是观测值的总数

四、案例研究：乌克兰战争对DAX的影响

在我上一篇文章的续篇中，我选择了德国最重要的股票指数DAX。

目的？ 衡量乌克兰战争对经济格局的影响。为此，我收集了从 2012 年初到 2023 年初的 DAX 数据，分析了在此期间的实际波动率。

4.1 准确估计波动率的重要性

估计波动性背后的方法在后续分析的精度和可靠性中起着关键作用。在接下来的部分中，我将把经典的预测技术与机器学习支持的尖端方法并列。目标？阐明机器学习模型在预测 1 年 2022 月 <> 日之后的市场变化方面的能力。

4.2 . 数据准备

我们将通过雅虎财经再次收集我们的数据，在这种情况下，我们提供必要的输入并访问数据。

stocks = '^GDAXI'
start = datetime.datetime(2012,1,1)
end = datetime.datetime(2023,1,1)
dax = yf.download(stocks, start, end, interval='1d')

数据似乎是这样的：

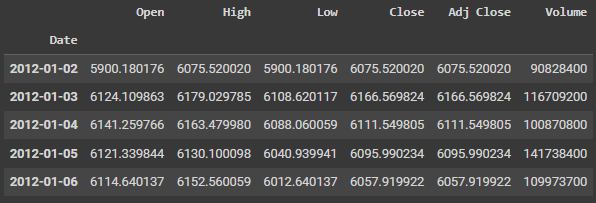
然后我们根据每日收盘价计算百分比变化。

ret = 100 * (dax.pct_change()[1:]["Adj Close"])
realized_vol = ret.rolling(5).std()

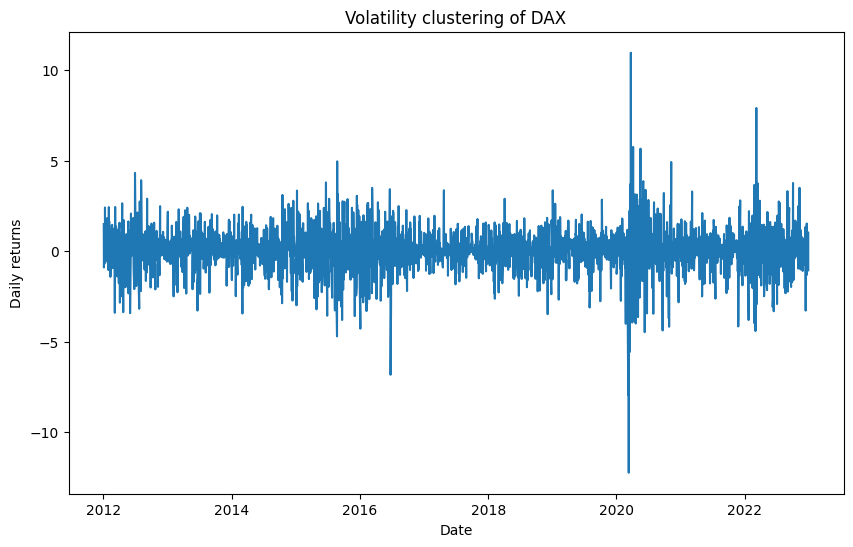
五、传统模式

5.1 ARCH拱门模型

ARCH 模型代表自回归条件变量方差，是用于估计方差的统计模型。它是由经济学家罗伯特·恩格尔于1982年提出的。ARCH模型在金融计量经济学中特别有用，用于对表现出时变波动性的金融时间序列进行建模，例如股票回报。

在许多金融时间序列中，大的变化往往伴随着大的变化（任何一个符号），小的变化往往伴随着小的变化。这种现象称为“波动性聚类”。传统的时间序列模型，如 ARMA（自回归移动平均线）旨在捕获时间序列平均值中的模式，但它们不能很好地处理波动性聚类。这就是 ARCH 模型的用武之地。

ARCH模型配方：

ARCH（q）模型可以表示为：

这里：

y_{t} 是时间 t 的返回
\epsilon_{t} 是时间 t 的误差项或白噪声
\sigma _{t}^{2} 是给定序列过去值的 t 的条件方差
z_{t} 是均值和单位方差为零的白噪声误差项
q 表示平方误差项的滞后数

主要思想是误差项 \epsilon_{t} 的方差不是恒定的，而是过去平方误差的函数。

n = (datetime.datetime.strptime('2023/1/1', "%Y/%m/%d") - datetime.datetime.strptime('2022/3/1', "%Y/%m/%d")).days
print(n)
split_date = ret.iloc[-n:].index
arch = arch_model(ret, mean='zero', vol='ARCH', p=1).fit(disp='off')
print(arch.summary())

bic_arch = []
for p in range(1, 5):
    arch = arch_model(ret, mean='zero', vol='ARCH', p=p)\
                      .fit(disp='off') 
    bic_arch.append(arch.bic)
    if arch.bic == np.min(bic_arch): 
            best_param = p
arch = arch_model(ret, mean='zero', vol='ARCH', p=best_param)\
           .fit(disp='off') 
print(arch.summary())
forecast = arch.forecast(start = split_date[0])
forecast_arch = forecast
rmse_arch = np.sqrt(mse(realized_vol[-n:]/100,
                        np.sqrt(forecast_arch.variance.iloc[-len(split_date):]/100)))
print("The RMSE value of ARCH model is {:.4f}".format(rmse_arch))

基于我们第一个模型的波动性预测结果就是这样。

5.2 GARCH模型

ARCH模型的自然扩展是GARCH（广义ARCH）模型。GARCH（p， q）模型将ARCH模型与自回归过程相结合，允许更灵活的结构来捕获时变波动性。

加奇模型

在这里，p 和 q 分别是 GARCH 和 ARCH 进程的阶数。

ARCH和GARCH模型都已成为建模和预测波动性的基础金融计量经济学。它们是风险管理、衍生品定价和许多其他金融领域的重要工具。

garch = arch_model(ret, mean='zero', vol='GARCH', p=1, o=0, q=1).fit(disp='off')
print(garch.summary())

基本 GARCH 模型摘要

bic_garch = []
for p in range(1, 5):
 for q in range(1, 5):
     garch = arch_model(ret, mean='zero',vol='GARCH', p=p, o=0, q=q)\
             .fit(disp='off')
     bic_garch.append(garch.bic)
     if garch.bic == np.min(bic_garch):
         best_param = p, q
garch = arch_model(ret, mean='zero', vol='GARCH',
                p=best_param[0], o=0, q=best_param[1])\
     .fit(disp='off')
print(garch.summary())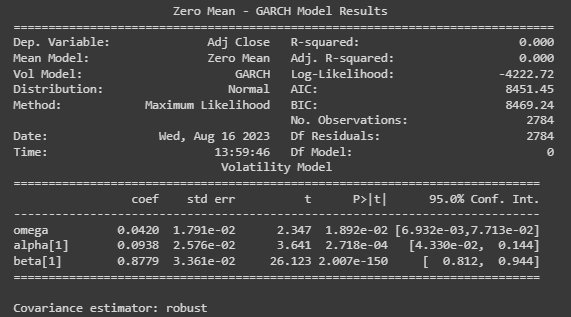

最佳 GARCH 模型摘要

forecast = garch.forecast(start=split_date[0])
forecast_garch = forecast
rmse_garch = np.sqrt(mse(realized_vol[-n:] / 100,
                         np.sqrt(forecast_garch \
                                 .variance.iloc[-len(split_date):]
                                 / 100)))
print('The RMSE value of GARCH model is {:.6f}'.format(rmse_garch))

加尔奇模型结果

GARCH模型很好地拟合了回报的波动性，部分原因是波动率聚类，部分原因是GARCH不假设回报是独立的，这允许它解释回报的轻盈特性。

5.3 GJR-GARCH （Glosten-Jagannathan-Runkle GARCH）：

GJR-GARCH模型由Glosten，Jagannathan和Runkle于1993年推出。它修改了GARCH模型，以允许波动性对正面和负面冲击的不同反应。

该模型可以表示为：

GJR GARCH模型

其中 gamma 控制公告的不对称性，如果：

伽马=0，对过去冲击的反应是一样的
伽马>0，对过去负面冲击的反应强于正面冲击。
伽马<0，对过去积极冲击的反应强于消极冲击。

bic_gjr_garch = []
for p in range(1,5):
    gjrgarch = arch_model(ret, mean='zero', p = p, o=1, q=q).fit(disp='off')
    bic_gjr_garch.append(gjrgarch.bic)
    if gjrgarch.bic == np.min(bic_gjr_garch):
        best_param = p,q
gjrgarch = arch_model(ret, mean='zero', p=best_param[0], q=best_param[1], o=1).fit(disp='off')
print(gjrgarch.summary())
forecast = gjrgarch.forecast(start=split_date[0])
forecast_gjrgarch = forecast

rmse_gjr_garch = np.sqrt(mse(realized_vol[-n:]/100,
                             np.sqrt(forecast_garch.variance.iloc[-len(split_date):]/100)))
print("The RMSE value of GJR GARCH model is {:.6f}".format(rmse_gjr_garch))

5.4 EGARCH （指数GARCH）

Nelson在1991年提出的EGARCH模型通过对条件方差的对数而不是方差本身进行建模，允许波动性对冲击响应的不对称性。这可确保条件方差保持正。

该模型可以表示为：

EGARCH 方程的主要区别在于，对数取方程左侧的方差。这表明杠杆效应，这意味着过去的资产回报与波动性之间存在负相关关系。

bic_egarch = []

for p in range(1,5):
    for q in range(1,5):
        egarch = arch_model(ret, mean='zero', vol='EGARCH',
                            p=p, q=q).fit(disp='off')
        bic_egarch.append(egarch.bic)
        if egarch.bic == np.min(bic_egarch):
            best_param = p,q
egarch = arch_model(ret, mean='zero', vol='EGARCH',
                    p=best_param[0], q=best_param[1]).fit(disp='off')
print(egarch.summary())

forecast = egarch.forecast(start=split_date[0])
forecast_egarch = forecast
rmse_egarch = np.sqrt(mse(realized_vol[-n:]/100,
                          np.sqrt(forecast_egarch.variance.iloc[-len(split_date):]/100)))
print("The RMSE value of EFARCH model is {:.6f}".format(rmse_egarch))

传统模式的成功案例

<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424">+-----------+--------+
|   MODEL   |  RMSE  |
+-----------+--------+
| ARCH      | 0,1207 |
| GARCH     | 0,1228 |
| GJR-GARCH | 0,1228 |
| EGARCH    | 0,1222 |
+-----------+--------+</span></span></span></span>

六. 机器学习模型

6.1 支持向量机

支持向量机（SVM）是一类最初为二元分类问题设计的监督学习算法。然而，它们的应用已经扩展到回归问题，称为支持向量回归（SVR），并且它们已经在包括波动性预测在内的广泛领域得到应用。

在金融计量经济学中，准确预测波动性对于风险管理、投资组合优化、期权定价和许多其他应用至关重要。如前所述，传统的波动率预测方法包括GARCH系列模型。最近，像SVM这样的机器学习技术已被用于提高预测的准确性。

内核技巧：包括 SVR 在内的 SVM 使用所谓的“内核技巧”将数据转换为更高维的空间，以找到最适合数据的超平面。常见的核包括线性、多项式和径向基函数（RBF）。在波动率预测的背景下，内核的选择会对预测的准确性产生重大影响。

SVM 在波动率分析中的优势：

非线性：金融时间序列数据通常具有线性模型可能无法有效捕获的非线性模式。SVM 由于其内核技巧可以处理非线性关系。

很少的假设：与一些传统的时间序列模型不同，SVM 不会对数据分布做出强有力的假设。

灵活性：SVM 可以整合各种功能，而不仅仅是过去的回报，从而为设计输入功能集提供灵活性。

from sklearn.svm import SVR
from scipy.stats import uniform as sp_rand
from sklearn.model_selection import RandomizedSearchCV

realized_vol = ret.rolling(5).std()
realized_vol = pd.DataFrame(realized_vol)
realized_vol.reset_index(drop=True, inplace=True)
retruns_svm = ret ** 2
returns_svm = retruns_svm.reset_index()
del returns_svm["Date"]
X = pd.concat([realized_vol, returns_svm], axis = 1, ignore_index=True)
X = X[4:].copy()
X = X.reset_index()
X.drop("index", axis = 1, inplace = True)
realized_vol = realized_vol.dropna().reset_index()
realized_vol.drop('index', axis=1, inplace=True)
svr_poly = SVR(kernel='poly',degree=2)
svr_lin  = SVR(kernel='linear')
svr_rbf  = SVR(kernel='rbf')

6.2 线性支持向量机

特征：线性 SVR 试图找到一个线性超平面，以最好地分离特征空间中的数据。

用例：适用于特征和目标变量之间具有线性关系的数据。

para_grid = {'gamma':sp_rand(),
             'C': sp_rand(),
             'epsilon': sp_rand()}
clf =RandomizedSearchCV(svr_lin, para_grid)
clf.fit(X.iloc[:-n].values,
        realized_vol.iloc[1:-(n-1)].values.reshape(-1,))
predict_svr_lin = clf.predict(X.iloc[-n:])
predict_svr_lin = pd.DataFrame(predict_svr_lin)
predict_svr_lin.index = ret.iloc[-n:].index
rmse_svr =np.sqrt(mse(realized_vol.iloc[-n:]/100,
                      predict_svr_lin/100))
print("The RMSE value of SVR with Linear Kernel is {:.4f}".format(rmse_svr))

6.3 RBF SVM

特点：RBF 内核可以将输入数据映射到无限维空间。它可以捕获非常复杂的关系，而无需指定确切的转换。从本质上讲，它考虑了实例之间的相似性，并且可以创建非线性决策边界。

用例：适用于没有明确线性或多项式关系的数据。它是一种受欢迎的选择，因为它具有处理各种数据形状的灵活性和能力。但是，仔细调整γ参数至关重要，因为它会极大地影响 SVR 的性能。

para_grid ={'gamma': sp_rand(),
         'C': sp_rand(),
         'epsilon': sp_rand()}
clf = RandomizedSearchCV(svr_rbf, para_grid)
clf.fit(X.iloc[:-n].values,
     realized_vol.iloc[1:-(n-1)].values.reshape(-1,))
predict_svr_rbf = clf.predict(X.iloc[-n:])
predict_svr_rbf = pd.DataFrame(predict_svr_rbf)
predict_svr_rbf.index = ret.iloc[-n:].index
rmse_svr_rbf = np.sqrt(mse(realized_vol.iloc[-n:] / 100,
                                    predict_svr_rbf / 100))
print('The RMSE value of SVR with RBF Kernel is  {:.6f}'
   .format(rmse_svr_rbf))

6.4 多项式支持向量机

特征：它使用多项式函数将输入数据映射到高维空间，然后尝试找到最适合此转换空间中的数据的超平面

用例：适用于特征与目标变量之间的关系为多项式或具有某种弯曲性质的情况。多项式的次数 d 决定了曲线的复杂性

para_grid = {'gamma': sp_rand(),
                     'C': sp_rand(),
                     'epsilon': sp_rand()}
clf = RandomizedSearchCV(svr_poly, para_grid)
clf.fit(X.iloc[:-n].values,
                 realized_vol.iloc[1:-(n-1)].values.reshape(-1,))
predict_svr_poly = clf.predict(X.iloc[-n:])
predict_svr_poly = pd.DataFrame(predict_svr_poly)
predict_svr_poly.index = ret.iloc[-n:].index
rmse_svr_poly = np.sqrt(mse(realized_vol.iloc[-n:] / 100,
                                     predict_svr_poly / 100))
print('The RMSE value of SVR with Polynomial Kernel is {:.6f}'\
               .format(rmse_svr_poly))

七、结论

了解波动性对于掌握金融市场的复杂性至关重要，主要是因为它为不确定性提供了一个可衡量的视角。这不仅仅是一个理论概念；而且是一个概念。它积极为大量金融模型提供信息，尤其是以风险为中心的金融模型。

虽然 ARCH 和 GARCH 等传统模型吸引了人们的注意，但它们的刚性结构往往限制了它们的适应性。令人振奋的是，现代方法，例如我们审查的SVM技术，产生了甚至优于最佳传统模型的有希望的结果。

资料引用

Andersen，Torben G.，Tim Bollerslev，Francis X. Diebold和Paul Labys。2003. “已实现波动率的建模和预测。”计量经济学 71 （2）：579–625。
波勒斯列夫，T. 1986。“广义自回归条件异方差。”计量经济学杂志 31 （3）： 307–327。3): 542–547.
布莱克，费舍尔。1976. “股票市场波动变化研究。”1976年美国统计协会商业和经济统计科会议记录。
卡拉桑、阿卜杜拉和埃斯玛·盖吉西斯。2020. “波动性预测和风险管理：SVR-GARCH 方法。”金融数据科学杂志 2 （4）： 85–104.
卡拉桑，阿卜杜拉（2021 年）。使用 Python 进行金融风险管理的机器学习 奥雷利
泰勒，S. 1986。对金融时间序列进行建模。奇切斯特：威利