188. 买卖股票的最佳时机IV
leetcode链接:188 题「买卖股票的最佳时机 IVopen in new window」
视频链接:动态规划来决定最佳时机,至多可以买卖K次!| LeetCode:188.买卖股票最佳时机4
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,
你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1]
输出:2
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,
这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3]
输出:7
解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出,
这笔交易所能获得利润 = 6-2 = 4 。
随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出,
这笔交易所能获得利润 = 3-0 = 3 。
接下来的解法来自labuladong的算法 ,从最难的188题入手,限制最多。用状态机的形式进行状态转移。
对于每天的股票,有三种选择:买,卖,不买也不卖。我们用 buy, sell, rest 表示这三种选择。但每次这三种状态不是随便选的:
- 因为
sell必须在buy之后(对于交易次数设置为无限次时,只能先卖掉手里的再买) buy必须在sell之后(手里有股票了才能卖)。- 那么
rest操作还应该分两种状态,一种是buy之后的rest(持有了股票),一种是sell之后的rest(没有持有股票)。 - 交易次数
k的限制,就是说你buy还只能在k > 0的前提下操作
- 确定dp数组的含义及下标
我们的dp数组应该是几维的?这个问题的「状态」有三个,第一个是天数,第二个是允许交易的最大次数,第三个是当前的持有状态(即之前说的 rest 的状态,我们不妨用 1 表示持有,0 表示没有持有)。然后我们用一个三维数组就可以装下这几种状态的全部组合:
dp[i][k][0 or 1]
0 <= i <= n - 1, 1 <= k <= K
n 为天数,大 K 为交易数的上限,0 和 1 代表是否持有股票。
此问题共 n × K × 2 种状态,全部穷举就能搞定。
for 0 <= i < n:
for 1 <= k <= K:
for s in {0, 1}:
dp[i][k][s] = max(buy, sell, rest)
比如说 dp[3][2][1] 的含义就是:今天是第三天,我现在手上持有着股票,至今最多进行 2 次交易。再比如 dp[2][3][0] 的含义:今天是第二天,我现在手上没有持有股票,至今最多进行 3 次交易。
我们想求的最终答案就是:dp[n - 1][k][0] ,因为最后一天卖出肯定比不卖出赚的多,因此求的不是dp[n-1][k][1] 。
- 确定递推公式
我们可以画出如下的状态转移图:
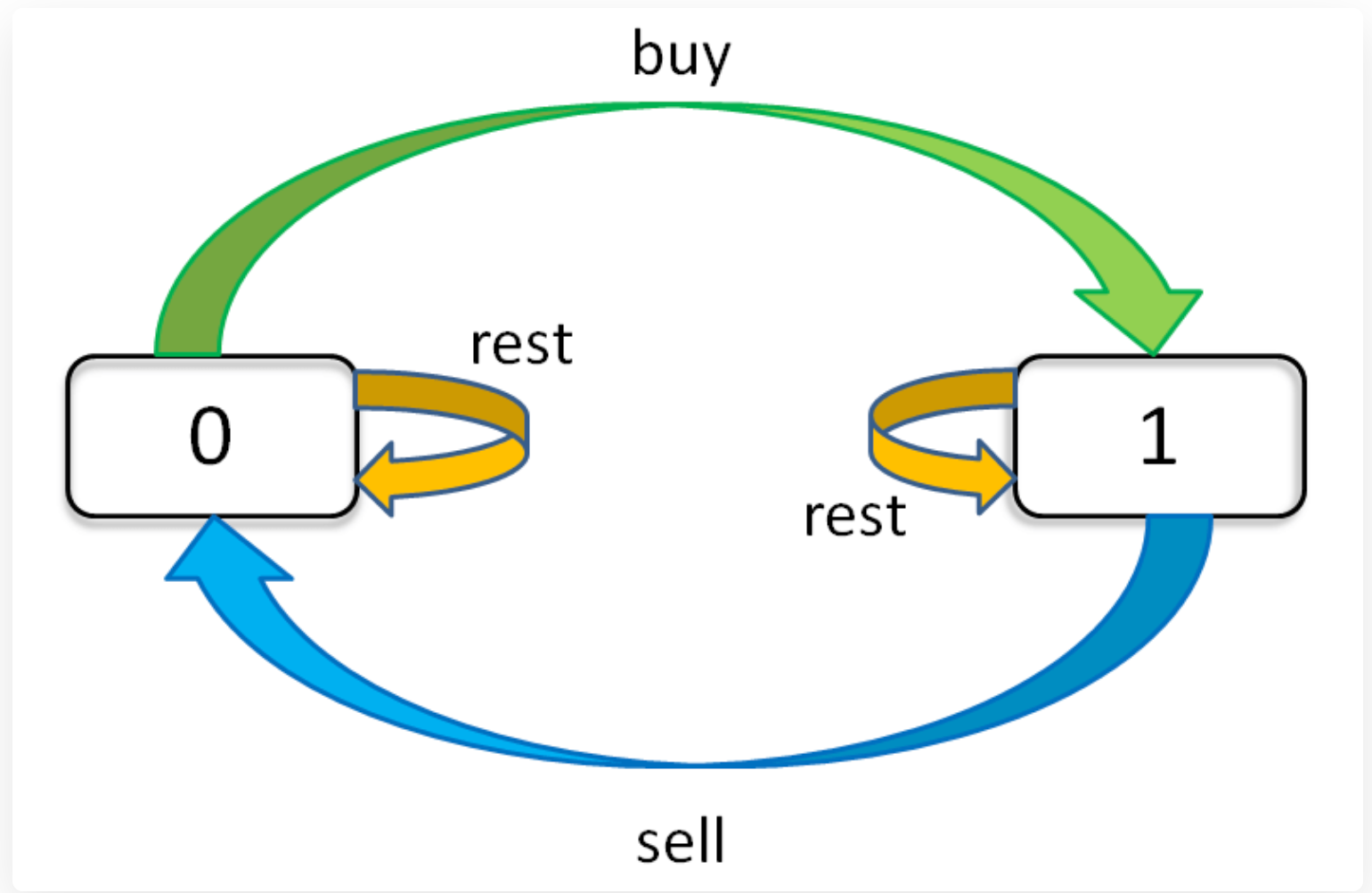
因此我们可以分两种状态:dp[i][k][0]和dp[i][k][1] 。
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
max( 今天选择 rest, 今天选择 sell )
解释:今天我没有持有股票,有两种可能,我从这两种可能中求最大利润:
1、我昨天就没有持有,且截至昨天最大交易次数限制为 k;然后我今天选择 rest,所以我今天还是没有持有,最大交易次数限制依然为 k。
2、我昨天持有股票,且截至昨天最大交易次数限制为 k;但是今天我 sell 了,所以我今天没有持有股票了,最大交易次数限制依然为 k。
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
max( 今天选择 rest, 今天选择 buy )
解释:今天我持有着股票,最大交易次数限制为 k,那么对于昨天来说,有两种可能,我从这两种可能中求最大利润:
1、我昨天就持有着股票,且截至昨天最大交易次数限制为 k;然后今天选择 rest,所以我今天还持有着股票,最大交易次数限制依然为 k。
2、我昨天本没有持有,且截至昨天最大交易次数限制为 k - 1;但今天我选择 buy,所以今天我就持有股票了,最大交易次数限制为 k。
- 状态
k的定义并不是「已进行的交易次数」,而是「最大交易次数的上限限制」。 - 在
sell的时候给k减小 1 和在buy的时候给k减小 1 是并不是等效,因为交易是从buy开始,如果buy的选择不改变交易次数k的话,会出现交易次数超出限制的的错误。也就是说买的时候k - 1卖的时候不减。
这是一个反向的过程,是推图的入边而不是出边。
- 确定dp初始化
dp[-1][...][0] = 0
解释:因为 i 是从 0 开始的,所以 i = -1 意味着还没有开始,这时候的利润当然是 0。
dp[-1][...][1] = -infinity
解释:还没开始的时候,是不可能持有股票的。
因为我们的算法要求一个最大值,所以初始值设为一个最小值,方便取最大值。
dp[...][0][0] = 0
解释:因为 k 是从 1 开始的,所以 k = 0 意味着根本不允许交易,这时候利润当然是 0。
dp[...][0][1] = -infinity
解释:不允许交易的情况下,是不可能持有股票的。
因为我们的算法要求一个最大值,所以初始值设为一个最小值,方便取最大值。
至于-1 怎么编程表示出来呢,负无穷怎么表示呢?这都是细节问题,有很多方法实现。
- 确定遍历顺序
因此天数是从小到大的,因此遍历顺序肯定是从前往后。
- 循环打印dp数组
这样我们就确定了买卖股票问题的框架,其他的题目都是这题的特殊情况。
最终代码(这里从123题的题解简化而来)
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int max_k = k;
vector<vector<vector<int>>> dp(prices.size(), vector<vector<int>>(max_k + 1, vector<int>(2,0)));
for(int i = 0; i < prices.size(); i++){
for(int k1 = max_k; k1 >= 1; k1--) {
if (i - 1 == -1) {
dp[i][k1][0] = 0;
dp[i][k1][1] = -prices[i];
continue;
}
dp[i][k1][0] = max(dp[i - 1][k1][0], dp[i - 1][k1][1] + prices[i]);
dp[i][k1][1] = max(dp[i - 1][k1][1], dp[i - 1][k1 - 1][0] - prices[i]);
}
}
return dp[prices.size() - 1][max_k][0];
}
};
123.买卖股票的最佳时机III
leetcode链接:力扣题目链接
视频链接:动态规划,股票至多买卖两次,怎么求? | LeetCode:123.买卖股票最佳时机III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,
这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,
这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出,
这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1]
输出:0
实际上,这题就是一般情况下k = 2的情况。
- dp数组含义及其下标
dp[i][k][0]/dp[i][k][1]表示第i天在最大贸易次数为k的情况下持有股票/不持有股票的最大利润。
- 确定递推公式
原始的状态转移方程,没有可化简的地方
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
- 确定dp数组的初始化
这里的max_k是自己设定的,最多交易两次,max_k = 2。注意这里的初始化是在for循环中进行的,在i = 0的时候初始化,因为k需要穷举。
for(int k = max_k; k >= 1; k--) {
if (i - 1 == -1) {
dp[i][k][0] = 0;
dp[i][k][1] = -prices[i];
continue;
}
- 确定遍历顺序
我们这里k是逆序的,比较符合常理:
你买股票,初始的「状态」是什么?应该是从第 0 天开始,而且还没有进行过买卖,所以最大交易次数限制 k 应该是 max_k;而随着「状态」的推移,你会进行交易,那么交易次数上限 k 应该不断减少,这样一想,k = max_k, k-- 的方式是比较合乎实际场景的。
- 打印dp数组
最终代码:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int max_k = 2;
vector<vector<vector<int>>> dp(prices.size(), vector<vector<int>>(max_k + 1, vector<int>(2,0)));
for(int i = 0; i < prices.size(); i++){
for(int k = max_k; k >= 1; k--) {
if (i - 1 == -1) {
dp[i][k][0] = 0;
dp[i][k][1] = -prices[i];
continue;
}
dp[i][k][0] = max(dp[i - 1][k][0], dp[i - 1][k][1] + prices[i]);
dp[i][k][1] = max(dp[i - 1][k][1], dp[i - 1][k - 1][0] - prices[i]);
}
}
return dp[prices.size() - 1][max_k][0];
}
};
空间复杂度简化版本(还是很难看懂):
// 空间复杂度优化版本
class Solution {
public:
int maxProfit_k_2(vector<int>& prices) {
// 状态转移方程:
// dp[i][2][0] = max(dp[i-1][2][0], dp[i-1][2][1] + prices[i])
// dp[i][2][1] = max(dp[i-1][2][1], dp[i-1][1][0] - prices[i])
// dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
// dp[i][1][1] = max(dp[i-1][1][1], -prices[i])
// base case
int dp_i10 = 0, dp_i11 = INT_MIN;
int dp_i20 = 0, dp_i21 = INT_MIN;
for (int price : prices) {
dp_i20 = max(dp_i20, dp_i21 + price);
dp_i21 = max(dp_i21, dp_i10 - price);
dp_i10 = max(dp_i10, dp_i11 + price);
dp_i11 = max(dp_i11, -price);
}
return dp_i20;
}
};
309. 买卖股票的最佳时机含冷冻期
leetcode链接:力扣题目链接
视频链接:动态规划来决定最佳时机,这次有冷冻期!| LeetCode:309.买卖股票的最佳时机含冷冻期
给定一个整数数组 prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
示例 2:
输入: prices = [1]
输出: 0
这题相比买卖股票II 添加了冷冻的限制,但其实k还是无穷的,把II的代码修改一下即可:
class Solution {
public:
int maxProfit(vector<int>& prices) {
vector<vector<int>> dp (prices.size(),vector<int>(2));
int cooldown = 1;//本题的冷却期为1天
dp[0][0] = 0;
dp[0][1] = -prices[0];
for(int i = 1; i < prices.size(); i++){
if(i - cooldown - 1 < 0){//防止数组越界,或者说在这段时间内i很短,不需要冷静期
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
dp[i][1] = max(dp[i-1][1], -prices[i]);
continue;
}
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
dp[i][1] = max(dp[i-1][1], dp[i- cooldown - 1][0] -prices[i]);
}
return dp[prices.size() - 1][0];
}
};
注意这里的dp[i][1]有变化,分析一下:dp[i][1]表示到状态1的两种情况,第一个是rest,从前一天开始就持有股票且不仍然不卖出,此时就是dp[i - 1][1],第二种情况是从前i - cooldown-1天买入,因为有冷冻期,故经过cooldown天才能在第二天买入。
714.买卖股票的最佳时机含手续费
leetcode链接:力扣题目链接
视频链接:动态规划来决定最佳时机,这次含手续费!| LeetCode:714.买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
示例 2:
输入: prices = [1]
输出: 0
这题加入了手续费的限制,k还是无限大,还是买卖股票II的变体。最终代码:
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
vector<vector<int>> dp (prices.size(),vector<int>(2));
dp[0][0] = 0;
dp[0][1] = -( prices[0]);
for(int i = 1; i < prices.size(); i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i] - fee);
dp[i][1] = max(dp[i-1][1], dp[i-1][0] -prices[i]);
}
return dp[prices.size() - 1][0];
}
};
注意这里手续费在一次交易(一次买入,一次卖出)中只需要交一次,故在卖出的时候交手续费就可以了,比较方便。
总结
- 买卖股票加入k之后,因为要穷举所有的状态,因此还要加一层循环对k进行穷举。
- 注意三维数组的vector写法:
vector<vector<vector<int>>> dp(prices.size(), vector<vector<int>>
(max_k + 1, vector<int>(2,0)));
- 无论是加入手续费还是冷静期,原理基本还是一样的。略微修改递归公式即可。若与天数相关就改变下标i,若与费用相关就改变price