常微分方程的龙格库塔显式与隐式解法

news2024/10/6 10:25:56
  • 好习惯，讲问题之前先来介绍一下最近生活状况。
    • 得到了 熟人的 熟人认证 很好 很荣幸了 属于是
  • 先上全部代码与效果图
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolve

class odesolver():
    def __init__(self, f, X_start=0, X_end=1, Y_start=1, dY_start=1, h=0.01):
        self.f = f
        self.h = h
        self.X = np.arange(X_start, X_end, self.h)
        self.Y = np.zeros(self.X.size)
        self.Y[0] = Y_start
        self.Y[1] = Y_start + self.h * dY_start
        self.tol = 1e-6
        
    def __str__(self):
        return f"y'(x) = f(x) = ({self.f}) only one variable"

    def RK4(self):
        for i in range(1, self.X.size):
            k1 = self.f(self.X[i-1], self.Y[i-1])
            k2 = self.f(self.X[i-1]+self.h/2, self.Y[i-1]+1/2*self.h*k1)
            k3 = self.f(self.X[i-1]+self.h/2, self.Y[i-1]+1/2*self.h*k2)
            k4 = self.f(self.X[i-1]+self.h, self.Y[i-1]+self.h*k3)
            self.Y[i] = self.Y[i-1] + 1/6 * self.h * (k1 + 2*k2 + 2*k3 + k4)
        return self.Y

    def IRK4(self):
        for i in range(1, self.X.size):
            f1 = lambda k:self.f(self.X[i-1]+self.h*(3-3**0.5)/6, \
                                self.Y[i-1]+k[0]/4*self.h+(3-2*3**0.5)/12*k[1]*self.h) - k[0] 
            f2 = lambda k:self.f(self.X[i-1]+self.h*(3+3**0.5)/6, \
                                self.Y[i-1]+k[1]/4*self.h+(3+2*3**0.5)/12*k[0]*self.h) - k[1]            
            sol = fsolve(lambda k: [f1(k), f2(k)], [0, 0])
            self.Y[i] = self.Y[i-1] + 1/2 * self.h * (sol[0] + sol[1])
        return self.Y

    def IRK6(self):
        for i in range(1, self.X.size):
            f1 = lambda k:self.h * self.f(self.X[i-1]+self.h*(5-15**0.5)/10, \
                                self.Y[i-1]+k[0]*5/36                +(10-3*15**0.5)/45*k[1]  +(25-6*15**0.5)/180*k[2]) - k[0] 
            f2 = lambda k:self.h * self.f(self.X[i-1]+self.h/2, \
                                self.Y[i-1]+k[0]*(10+3*15**0.5)/72   +2/9*k[1]                +(10-3*15**0.5)/12*k[2]) - k[1]            
            f3 = lambda k:self.h * self.f(self.X[i-1]+self.h*(5+15**0.5)/10, \
                                self.Y[i-1]+k[0]*(25+6*15**0.5)/180  +(10+3*15**0.5)/45*k[1]  +5/36*k[2]) - k[2]            
            sol = fsolve(lambda k: [f1(k), f2(k), f3(k)], [0, 0, 0])
            self.Y[i] = self.Y[i-1] + (5/18*sol[0] + 4/9*sol[1] + 5/18*sol[2])
        return self.Y

    def Milne(self):
        for i in range(1, self.X.size):
            k1 = self.h * self.f(self.X[i-1], self.Y[i-1])
            k2 = self.h * self.f(self.X[i-1]+self.h/3, self.Y[i-1]+1/3*k1)
            k3 = self.h * self.f(self.X[i-1]+self.h*2/3, self.Y[i-1]+1/3*k1+k2)
            k4 = self.h * self.f(self.X[i-1]+self.h, self.Y[i-1]+k1-k2+k3)
            self.Y[i] = self.Y[i-1] + 1/8 * (k1 + 8*k2 + 3*k3 + k4)
        return self.Y

    def Kutta(self):
        for i in range(1, self.X.size):
            k1 = self.h * self.f(self.X[i-1], self.Y[i-1])
            k2 = self.h * self.f(self.X[i-1]+self.h/2, self.Y[i-1]+1/2*k1)
            k3 = self.h * self.f(self.X[i-1]+self.h/2, self.Y[i-1]+(2**0.5-1)/2*k1+(1-2**0.5/2)*k2)
            k4 = self.h * self.f(self.X[i-1]+self.h, self.Y[i-1]-2**0.5/2*k2+(1+2**0.5/2)*k3)
            self.Y[i] = self.Y[i-1] + 1/6 * (k1 + (2-2**0.5)*k2 + (2+2**0.5)*k3 + k4)
        return self.Y
    
c = odesolver(f=lambda x,y:x*y)
x = np.arange(0, 1, 0.01)
y1 = c.RK4()
y2 = c.IRK4()
y3 = c.IRK6()
y4 = c.Milne()
y5 = c.Kutta()
f_true = lambda x:np.exp(x**2/2)
y_true = f_true(x)

plt.plot(x, y1, label="RK4")
plt.plot(x, y2, label="IRK4")
plt.plot(x, y3, label="IRK6")
plt.plot(x, y4, label="Milne")
plt.plot(x, y5, label="Kutta")
plt.plot(x, y_true, label="true")
plt.legend()
plt.pause(0.01)
  • 你就说这个代码写得规不规范，整不整齐
  • 效果图

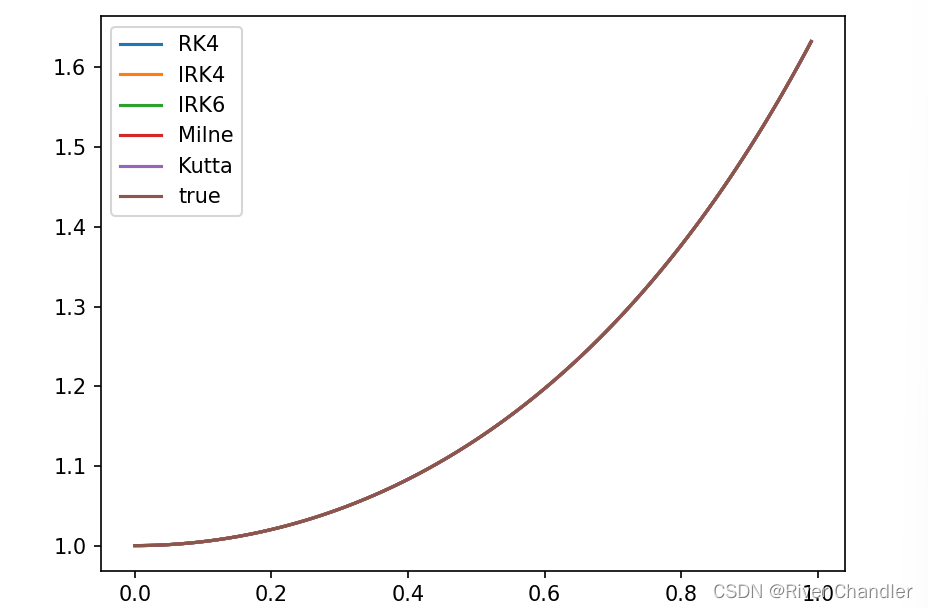
 常微分方程的隐式与显式解法详解

  • 说到这一点，就必须将一个故事
    • 有天 博主在网上逛 但是发现这里竟然没有一篇能完整得给出解微分方程隐式方法的完整代码的博客，于是决定写一篇
  • 什么是显式方法呢，就是每一步的值仅有上一步或前几步有关
  • 什么是隐式方法呢，就是对于每一步必须要求解一个方程以得到该步的近似值
  • 很好，我觉得我解释得极其精确无误了

常用公式

四级四阶显式 Runge - Kutta 方法

\begin{matrix} y_{n+1}=y_n+\frac{1}{6}(k_1+2k_2+2k_3+k_4)\\ k_1=f(x_n,y_n)\\ k_2=f(x_n+\frac{h}{2},y_n+\frac{hk_1}{2})\\ k_3=f(x_n+\frac{h}{2},y_n+\frac{hk_2}{2})\\ k_4=f(x_n+h,y_i+hk_3) \end{matrix}

二级四阶隐式 Runge - Kutta 方法

\begin{matrix} y_{n+1}=y_n+\frac{1}{2}(k_1+k_2)\\ k_1 = f(x_n+\frac{3-\sqrt{3}}{6}h,y_i+\frac{k_1h}{4}+\frac{3-2\sqrt{3}}{12}k_2h)\\ k_2 = f(x_n+\frac{3+\sqrt{3}}{6}h,y_i+\frac{k_2h}{4}+\frac{3+2\sqrt{3}}{12}k_1h) \end{matrix}

三级六阶隐式 Runge - Kutta 方法

\begin{matrix} y_{n+1}=y_n+\frac{5}{18}k_1+\frac{4}{9}k_2+\frac{5}{18}k_3\\ k_1=hf(x_n+\frac{5-\sqrt{15}}{10}h,y_n+\frac{5}{36}k_1+\frac{10-3\sqrt{15}}{45}k_2+\frac{25-6\sqrt{15}}{180}k_3)\\ k_2=hf(x_n+\frac{h}{2},y_n+\frac{10+3\sqrt{15}}{72}k_1+\frac{2}{9}k_2+\frac{10-3\sqrt{15}}{12}k_3)\\ k_3=hf(x_n+\frac{5+\sqrt{15}}{10}h,y_n+\frac{25+6\sqrt{15}}{180}k_1+\frac{10+3\sqrt{15}}{45}k_2+\frac{5}{36}k_3) \end{matrix}

四级四阶 Kutta 方法

\left\{\begin{matrix} y_{n+1}=y_n + \frac{1}{8}(k_1+8k_2+3k_3+k_4)\\ k_1=hf(x_n,y_n)\\ k_2=hf(x_n+\frac{h}{3},y_n+\frac{k_1}{3})\\ k_3=hf(x_n+\frac{2h}{3},y_n+\frac{k_1}{3}+k_2)\\ k_4=hf(x_n+h,y_n+k_1-k_2+k_3) \end{matrix}\right.

四级四阶 Milne 方法

\left\{\begin{matrix} y_{n+1}=y_n + \frac{1}{6}(k_1+(2-\sqrt{2})k_2+(2+\sqrt{2})k_3+k_4)\\ k_1=hf(x_n,y_n)\\ k_2=hf(x_n+\frac{h}{2},y_n+\frac{k_1}{2})\\ k_3=hf(x_n+\frac{h}{2},y_n+\frac{\sqrt{2}-1}{2}k_1+(1-\frac{\sqrt{2}}{2})k_2)\\ k_4=hf(x_n+h,y_n-\frac{\sqrt{2}}{2}k_2+(1+\frac{\sqrt{2}}{2})k_3) \end{matrix}\right.

求根方法

  • 这个我以后再讲，前面陆陆续续讲过几次，在特征值里面，请大家自行翻阅

常微分方程组的隐式与显式解法

  • 这个就比较酷炫了，因为写起来代码会稍微有一点问题
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolve
 
class odessolver():
    def __init__(self, f, Y_start=np.array([0, 1]), dY_start=np.array([0, 0]), \
                 X_start=0, X_end=1, h=0.01):

        self.f = f
        self.h = h
        self.X = np.arange(X_start, X_end, self.h)
        self.n = Y_start.size
        self.Y = np.zeros((self.n, self.X.size))
        #第一个参数表示元 第二个参数表示变量
        self.Y[:, 0] = Y_start
        self.Y[:, 1] = Y_start + self.h * dY_start
        self.tol = 1e-6
        
    def __str__(self):
        return f"y'(x) = f(x) = ({self.f}) variables"
 
    def RK4(self):
        for i in range(1, self.X.size):
            k1 = self.f(self.X[i-1]           , self.Y[:, i-1])
            k2 = self.f(self.X[i-1] +self.h/2 , self.Y[:, i-1]+1/2*self.h*k1)
            k3 = self.f(self.X[i-1] +self.h/2 , self.Y[:, i-1]+1/2*self.h*k2)
            k4 = self.f(self.X[i-1] +self.h   , self.Y[:, i-1]+    self.h*k3)
            self.Y[:, i] = self.Y[:, i-1] +self.h/6 * (k1 + 2*k2 + 2*k3 + k4)
        return self.Y

    def Milne(self):
        for i in range(1, self.X.size):
            k1 = self.h * self.f(self.X[i-1]              , self.Y[:, i-1])
            k2 = self.h * self.f(self.X[i-1] +self.h/3    , self.Y[:, i-1] + 1/3*k1)
            k3 = self.h * self.f(self.X[i-1] +self.h*2/3  , self.Y[:, i-1] + 1/3*k1+k2)
            k4 = self.h * self.f(self.X[i-1] +self.h      , self.Y[:, i-1] + k1 - k2 + k3)
            self.Y[:, i] = self.Y[:, i-1] + 1/8 * (k1 + 8*k2 + 3*k3 + k4)
        return self.Y

    def Kutta(self):
        for i in range(1, self.X.size):
            k1 = self.h * self.f(self.X[i-1]           , self.Y[:, i-1])
            k2 = self.h * self.f(self.X[i-1]+self.h/2  , self.Y[:, i-1] + k1/2)
            k3 = self.h * self.f(self.X[i-1]+self.h/2  , self.Y[:, i-1] + (2**0.5-1)/2*k1+(1-2**0.5/2)*k2)
            k4 = self.h * self.f(self.X[i-1]+self.h    , self.Y[:, i-1] - 2**0.5/2*k2+(1+2**0.5/2)*k3)
            self.Y[:, i] = self.Y[:, i-1] + 1/6 * (k1 + (2-2**0.5)*k2 + (2+2**0.5)*k3 + k4)
        return self.Y

    def IRK4(self):
            
        for i in range(1, self.X.size):
            def f1(k1, k2):
                f1_x = self.X[i-1] + self.h*(3-3**0.5)/6
                f1_y = self.Y[:, i-1]+k1/4*self.h+(3-2*3**0.5)/12*k2*self.h
                f1_res = self.f(f1_x, f1_y)
                return np.array([f1_res[i] for i in range(self.n)])

            def f2(k1, k2):
                f2_x = self.X[i-1] + self.h*(3+3**0.5)/6
                f2_y = self.Y[:, i-1]+k2/4*self.h+(3+2*3**0.5)/12*k1*self.h
                f2_res = self.f(f2_x, f2_y)
                return np.array([f2_res[i] for i in range(self.n)])              
                
            def func(k):
                k1 = np.array([k[i] for i in range(self.n)])
                k2 = np.array([k[i+self.n] for i in range(self.n)])
                
                doc = []
                for i in range(self.n):
                    doc.append((k1 - f1(k1, k2))[i])
                for i in range(self.n):
                    doc.append((k2 - f2(k1, k2))[i])
                return doc
            
            sol = fsolve(func, np.zeros(self.n*2))
            self.Y[:, i] = self.Y[:, i-1] + 1/2 * self.h * (sol[:self.n] + sol[self.n:])
        return self.Y

    def IRK6(self):
            
        for i in range(1, self.X.size):
            def f1(k1, k2, k3):
                f1_x = self.X[i-1] + self.h*(5-15**0.5)/10
                f1_y = self.Y[:, i-1]+k1*5/36+(10-3*15**0.5)/45*k2+(25-6*15**0.5)/180*k3
                f1_res = self.f(f1_x, f1_y)
                return np.array([f1_res[i] for i in range(self.n)])

            def f2(k1, k2, k3):
                f2_x = self.X[i-1] + self.h/2
                f2_y = self.Y[:, i-1]+k1*(10+3*15**0.5)/72+2/9*k2+(10-3*15**0.5)/12*k3
                f2_res = self.f(f2_x, f2_y)
                return np.array([f2_res[i] for i in range(self.n)])              

            def f3(k1, k2, k3):
                f3_x = self.X[i-1] + self.h*(5+15**0.5)/10
                f3_y = self.Y[:, i-1]+k1*(25+6*15**0.5)/180+(10+3*15**0.5)/45*k2+5/36*k3
                f3_res = self.f(f3_x, f3_y)
                return np.array([f3_res[i] for i in range(self.n)]) 

                
            def func(k):
                k1 = np.array([k[i] for i in range(self.n)])
                k2 = np.array([k[i+self.n] for i in range(self.n)])
                k3 = np.array([k[i+2*self.n] for i in range(self.n)])
                
                doc = []
                for i in range(self.n):
                    doc.append((k1 - self.h * f1(k1, k2, k3))[i])
                for i in range(self.n):
                    doc.append((k2 - self.h * f2(k1, k2, k3))[i])
                for i in range(self.n):
                    doc.append((k3 - self.h * f3(k1, k2, k3))[i])
                return doc
            
            sol = fsolve(func, np.zeros(self.n*3))
            self.Y[:, i] = self.Y[:, i-1] +\
                           5/18 * sol[:self.n] +\
                           4/9 * sol[self.n:2*self.n] +\
                           5/18 * sol[2*self.n:]
            

        return self.Y


def test_fun(x, Y):   
    return np.array([x**2+Y[1]**3, -Y[0]**2])

c = odessolver(test_fun)
x = np.arange(0, 1, 0.01)

y1 = c.Kutta()
plt.plot(x, y1[0, :], label="Kutta1")
plt.plot(x, y1[1, :], label="Kutta2")

y2 = c.Milne()
plt.plot(x, y1[0, :], label="Milne1")
plt.plot(x, y1[1, :], label="Milne2")

y3 = c.RK4()
x = np.arange(0, 1, 0.01)
plt.plot(x, y1[0, :], label="RK41")
plt.plot(x, y1[1, :], label="RK42")

y4 = c.IRK4()
x = np.arange(0, 1, 0.01)
plt.plot(x, y4[0, :], label="IRK41")
plt.plot(x, y4[1, :], label="IRK42")

y5 = c.IRK6()
x = np.arange(0, 1, 0.01)
plt.plot(x, y5[0, :], label="IRK61")
plt.plot(x, y5[1, :], label="IRK62")


plt.legend()
plt.pause(0.01)

数值实验

数值实验一

\begin{pmatrix} y_1'\\ y_2' \end{pmatrix}=\begin{matrix} x^2+y_2^3\\ -y_1^2 \end{matrix}    Y_0=\begin{pmatrix} 0\\ 1 \end{pmatrix}

  • 这一点说明 Milne方法还是有一点不精确的 

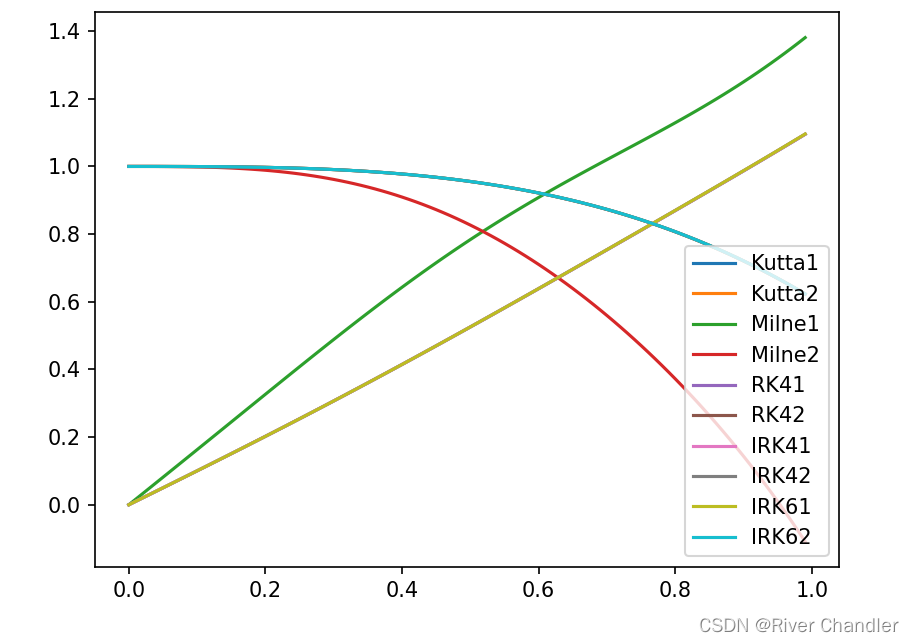
数值实验二

\begin{pmatrix} y_1'\\ y_2' \\y_3'\\ y_4' \end{pmatrix}=\begin{matrix} x^2+y_2^3\\ -y_1^2\\y_2-y_4\\y_2y_3 \end{matrix}  Y_0=\begin{pmatrix} 0\\ 1\\5 \\7 \end{pmatrix}

  • 这一点说明 RK4 IRK4 IRK6 效果都十分牛

  • Kutta 方法 和 Milne 方法 效果就不好了
  • 总体概览图 

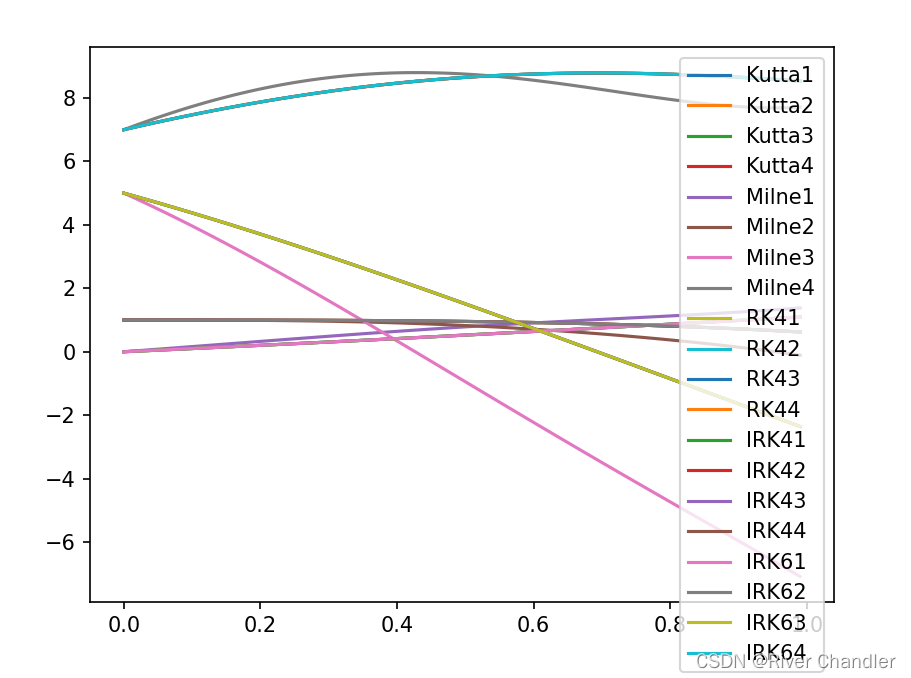
含参常微分方程组的求解

  • 数学模型中我们会常见到带参数的微分方程组，以三级六阶龙格库塔方法为例，我们对这玩意进行一下小小的微操
    def IRK6(self, Param=None):

        for i in range(1, self.X.size):
            def f1(k1, k2, k3):
                f1_x = self.X[i-1] + self.h*(5-15**0.5)/10
                f1_y = self.Y[:, i-1]+k1*5/36+(10-3*15**0.5)/45*k2+(25-6*15**0.5)/180*k3
                f1_res = self.f(f1_x, f1_y, param = Param)
                return np.array([f1_res[i] for i in range(self.n)])

            def f2(k1, k2, k3):
                f2_x = self.X[i-1] + self.h/2
                f2_y = self.Y[:, i-1]+k1*(10+3*15**0.5)/72+2/9*k2+(10-3*15**0.5)/12*k3
                f2_res = self.f(f2_x, f2_y, param = Param)
                return np.array([f2_res[i] for i in range(self.n)])              

            def f3(k1, k2, k3):
                f3_x = self.X[i-1] + self.h*(5+15**0.5)/10
                f3_y = self.Y[:, i-1]+k1*(25+6*15**0.5)/180+(10+3*15**0.5)/45*k2+5/36*k3
                f3_res = self.f(f3_x, f3_y, param = Param)
                return np.array([f3_res[i] for i in range(self.n)]) 

                
            def func(k):
                k1 = np.array([k[i] for i in range(self.n)])
                k2 = np.array([k[i+self.n] for i in range(self.n)])
                k3 = np.array([k[i+2*self.n] for i in range(self.n)])
                
                doc = []
                for i in range(self.n):
                    doc.append((k1 - self.h * f1(k1, k2, k3))[i])
                for i in range(self.n):
                    doc.append((k2 - self.h * f2(k1, k2, k3))[i])
                for i in range(self.n):
                    doc.append((k3 - self.h * f3(k1, k2, k3))[i])
                return doc
            
            sol = fsolve(func, np.zeros(self.n*3))
            self.Y[:, i] = self.Y[:, i-1] +\
                           5/18 * sol[:self.n] +\
                           4/9 * sol[self.n:2*self.n] +\
                           5/18 * sol[2*self.n:]
            

        return self.Y
  • 而后
def test_fun(x, Y, param=[1, 1, 1]):
    a, b, c = param
    return np.array([a*x**2+b*Y[1]**3, -c*Y[0]**2])

##c = odessolver(test_fun)

含参常微分方程组求解的并行加速

from paraodessolver import *
import multiprocessing as mp
import datetime

c = odessolver(test_fun)

def final_fun(name,para):
    for num in para:
        result = c.IRK6(Param=num) 
    return {name:result}
    
if __name__ == '__main__':
 
    start_time = datetime.datetime.now() 
    num_cores = int(mp.cpu_count())    
    pool = mp.Pool(num_cores)
    param_dict = {'task1': [[1, 2, 4],[2, 4, 5],[3, 4, 1]],
                  'task2': [[3, 3, 3],[2, 2, 2],[1, 1, 6]],
                  'task3': [[8, 6, 4],[3, 5, 6],[1, 2, 8]],
                  'task4': [[9, 8, 5],[6, 6, 7],[3, 6, 9]],
                  'task5': [[1, 2, 4],[2, 4, 5],[3, 4, 1]],
                  'task6': [[3, 3, 3],[2, 2, 2],[1, 1, 6]],
                  'task7': [[8, 6, 4],[3, 5, 6],[1, 2, 8]],
                  'task8': [[9, 8, 5],[6, 6, 7],[3, 6, 9]]}
    
    results = [pool.apply_async(final_fun, args=(name, param)) for name, param in param_dict.items()]
    results = [p.get() for p in results]
    end_time = datetime.datetime.now()
    use_time = (end_time - start_time).total_seconds()
    print("多进程计算 共消耗: " + "{:.2f}".format(use_time) + " 秒")
##    print(results)

    start_time = datetime.datetime.now() 
    for i in range(3):
         c.IRK6(Param=[1, 2, 3])
    end_time = datetime.datetime.now()
    print("单进程计算 共消耗: " + "{:.2f}".format(use_time) + " 秒")

多进程计算 共消耗: 2.26 秒
单进程计算 共消耗: 2.26 秒
  • 效率提高了区区八倍而已，并不是很强的啦


多进程计算 共消耗: 2.16 秒
单进程计算 共消耗: 2.16 秒

多进程计算 共消耗: 2.68 秒
单进程计算 共消耗: 2.68 秒

多进程计算 共消耗: 2.58 秒
单进程计算 共消耗: 2.58 秒

多进程计算 共消耗: 2.55 秒
单进程计算 共消耗: 2.55 秒

多进程计算 共消耗: 2.53 秒
单进程计算 共消耗: 2.53 秒

  • 记得给电脑降温，这很重要

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/946499.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

树与图c++

树与图c++

1.树 前言 本文主要介绍的数据结构之树型结构的相关知识，树型数据结构是面试官面试的时候非常喜欢考的一种数据结构，树形结构的遍历也是大厂笔试非常喜欢设置的考点，这些内容都会在本篇文章中进行详细的介绍，并且还会介绍一些常…
阅读更多...
Doris架构中包含哪些技术？

Doris架构中包含哪些技术？

Doris主要整合了Google Mesa(数据模型)，Apache Impala(MPP Query Engine)和Apache ORCFile (存储格式，编码和压缩)的技术。 为什么要将这三种技术整合? Mesa可以满足我们许多存储需求的需求，但是Mesa本身不提供SQL查询引擎。 Impala是一个…
阅读更多...
【IEEE会议】第六届IEEE机械工程与智能制造国际会议（WCMEIM 2023）

【IEEE会议】第六届IEEE机械工程与智能制造国际会议（WCMEIM 2023）

2023年第六届IEEE机械工程与智能制造国际会议（WCMEIM 2023） 2023 6th World Conference on Mechanical Engineering and Intelligent Manufacturing 坚定不移加快发展智能制造，推进信息化和工业化深度融合，实现制造业质量变革、…
阅读更多...
uniapp 配置小程序分包

uniapp 配置小程序分包

分包可以减少小程序首次启动时的加载时间 分包页面（例如：商品详情页、商品列表页）。在 uni-app 项目中，配置分包的步骤如下： 1、右键点击根目录，新建，点击创建分包的根目录，命名为 …
阅读更多...
YOLO目标检测——Kylberg纹理数据集下载分享

YOLO目标检测——Kylberg纹理数据集下载分享

Kylberg纹理数据集共同4640图片，可应用于：纹理分类与识别、材料识别与质检、医学图像分析、地质勘探与地表覆盖分类等等 数据集点击下载：YOLO目标检测Kylberg纹理数据集4640图片.rar
阅读更多...
《开发实战》11 | 空值处理：分不清楚的null和恼人的空指针

《开发实战》11 | 空值处理：分不清楚的null和恼人的空指针

11 | 空值处理：分不清楚的null和恼人的空指针 修复和定位恼人的空指针问题 NullPointerException 是 Java 代码中最常见的异常，最可能出现的场景归为以下5 种： 参数值是 Integer 等包装类型，使用时因为自动拆箱出现了空指针异常…
阅读更多...
02调制+滤波器+冲激函数的傅立叶变换

02调制+滤波器+冲激函数的傅立叶变换

目录 一、调制方式 1.1 什么是调制？ 1.2 为什么要调制？ 1.3 如何调制？ 1.4 调制包含的信号类型？ 1. 消息信号 2. 载波信号 3. 调制信号 1.5 调制类型？ 1. 调幅 2. 调频 3. 调相 4. 模拟脉冲调制 5. 脉冲…
阅读更多...
07:STM32----ADC模数转化器

07:STM32----ADC模数转化器

目录 1:简历 2:逐次逼近型ADC 3:ADC基本结构 4:输入通道 5:规则组的4种转换模式 1:单次转化,非扫描模式 2:连续转化,非扫描模式 3:单次转化,扫描模式 4:单次转化,扫描模式 6:触发控制 7:数据对齐 8:转化时间 9:校准 10:ADC的硬件电路 A: AD单通道 1:连接图 2:函…
阅读更多...
单变量图的类型与直方图绘图基础

单变量图的类型与直方图绘图基础

文章目录 单变量图的类型1.直方图（histogram plot）2.密度图（density plot）3.Q-Q 图（Quantile- Quantile plot，又称分位图）4.P-P 图（Probability-Probability plot）5.经验…
阅读更多...
illegal cyclic inheritance involving trait Iterable_2种解决方式

illegal cyclic inheritance involving trait Iterable_2种解决方式

一、报错内容 /Users/liyangda/Code/DemoProject/demo-scala/src/scala/old04/T4.scala:11:20 illegal cyclic inheritance involving trait Iterableval value List(1, 2, 3, 4, 5, 6, 7, 8)二、问题解决 1、方式一：降低scala版本 可以选择降低Scala的版本&…
阅读更多...
《探花交友》之开篇

《探花交友》之开篇

《探花交友》 功能介绍项目介绍工程搭建短信验证码实现用户登录功能前后端开发视频及相关资源领取Q作者 1、功能介绍 探花交友是一个陌生人的在线交友平台，在该平台中可以搜索附近的人，查看好友动态，平台还会通过大数据计算进行智能推荐&a…
阅读更多...
若依自定义详情页（传多个参数）

若依自定义详情页（传多个参数）

【版权所有，文章允许转载，但须以链接方式注明源地址，否则追究法律责任】【创作不易，点个赞就是对我最大的支持】 前言 仅作为学习笔记，供大家参考 总结的不错的话，记得点赞收藏关注哦！ 不知道…
阅读更多...
gerrit 如何提交进行review

gerrit 如何提交进行review

前言 本文主要介绍如何使用gerrit进行review。 下述所有流程都是参考： https://gerrit-review.googlesource.com/Documentation/intro-gerrit-walkthrough.html 先给一个commit后但是还没有push上去的一个办法： git reset --hard HEAD^可以多次reset.…
阅读更多...
5V升压充电16.8V芯片充电管理IC

5V升压充电16.8V芯片充电管理IC

航誉微HU5912四节锂电池升压充电IC 概要 HU5912是一款 5V输入，支持四节锂电池的升压充电管理 IC。 HU5912 ，采用异步开关架构，使其在应用时仅需 要极少的外围器件，可有效减少整体方案尺寸，降低 BOM 成本。 HU5912…
阅读更多...
腾讯云便宜购买指南（腾讯云怎样购买划算）

腾讯云便宜购买指南（腾讯云怎样购买划算）

腾讯云是国内知名的云计算服务商，拥有广泛的应用和用户群体。对于有需要的用户来说，怎样便宜购买腾讯云产品是一个值得关注的问题，下面给大家分享腾讯云便宜购买指南。 腾讯云便宜购买指南：1、新用户专属礼包；2、老用户…
阅读更多...
网路日志服务器

网路日志服务器

网络日志服务器是用于集中存储、管理和分析网络设备生成的日志数据的服务器。它扮演着收集、存储和分析网络日志的关键角色，对于网络安全、故障排除和性能优化等方面具有重要意义。 网络日志服务器的工作原理是通过与网络设备建立连接，接收并保存设备生成…
阅读更多...
《人月神话》：chapter 4 系统设计中的“专制”和“民主”

《人月神话》：chapter 4 系统设计中的“专制”和“民主”

以下总结来自于《人月神话》 第四章 ：贵族制，民主制和系统设计 系统设计中最重要的因素：概念完整性 1.设计必须由一个人或者具有共识的小型团队来完成 2.大型系统架构设计与具体实现相分离 3.必须有人控制概念，确保完整性&…
阅读更多...
WebSocket- 前端篇

WebSocket- 前端篇

官网代码 // 为了浏览器兼容websocketconst WebSocket window.WebSocket || window.MozWebSocket// 创建连接 this.socket new WebSocket(ws://xxx)// 连接成功this.socket.onopen (res)>{console.log(websocket 连接成功)this.socket.send(入参字段) // 传递的参数字段}…
阅读更多...
【Android】AES解密抛出异常Cipher functions:OPENSSL_internal:WRONG_FINAL_BLOCK_LENGTH

【Android】AES解密抛出异常Cipher functions:OPENSSL_internal:WRONG_FINAL_BLOCK_LENGTH

Java使用AES加密的时候没得问题，但是在解密的时候就出错了，一起来找找原因吧。 首先，Java运行的代码如下，使用AES加解密 Cipher cipher Cipher.getInstance("AES/CBC/NOPadding"); //...主要问题 可调试运行控制台抛…
阅读更多...
Figma怎么导出源文件，超详细教程来了

Figma怎么导出源文件，超详细教程来了

Figma怎么导出源文件，超详细教程来了要说近几年话题最多的界面设计软件，Figma当之无愧。用一句话去定义Figma，它是一款基于浏览器的全能型设计工具。Figma允许设计师、开发者和其他团队成员无论身在何处，都可以共同协作创建和编辑…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023