目录
查找的基本概念
线性表的查找
顺序查找
折半查找(二分或对分查找)
分块查找(索引顺序查找)
树表的查找
二叉排序树
定义:
二叉排序树的查找:
二叉排序树的插入:
二叉排序树的创建:
二叉排序树的删除:
平衡二叉树
B-树
B+树
散列表的查找
散列表的基本概念
散列函数的构造方法
散列表的查找
查找的基本概念
查找表:查找表是由同一类型的数据元素(或记录)构成的集合。由于”集合“中的数据元素之间存在着完全松散的关系,因此查找表是一种非常灵便的数据结构,可以用其他的数据结构来实现。
关键字:关键字是数据元素(或记录)中某个数据项的值,用它可以标识一个数据元素(或记录);若此关键字可以唯一的标识一个记录,则称此关键字为主关键字(对不同的记录,其主关键字均不同)。反之,称用以识别若干记录的关键字为次关键字。当数据元素只有一个数据项时,其关键字即为该数据元素的值。
查找:查找是指根据给定的某个值,在查找表中确定一个其关键字等于给定值的记录或数据元素。若表中存在这样的一个记录,则称查找成功,此时查找的结果可给出整个记录的信息,或指示该记录在查找表中的位置;若表中不存在关键字等于给定值的记录,则称查找不成功,此时查找的结果可给出一个“空”记录或“空”指针。
动态查找表:若在查找的同时对表做修改操作(插入删除等)则相应的表称之为动态查找表;否则称之为静态查找表
平均查找长度ASL(查找算法的评价指标):为确定记录在查找表中的位置,需和给定值进行比较的关键字个数的期望值,称为查找算法在查找成功时的平均查找长度(Average Search Length)
线性表的查找
顺序查找
顺序查找的查找过程:从表的一端开始,依次将记录的关键字和给定的值进行比较,若某个记录的关键字和给定值相等,则查找成功;反之,若扫描整个表后,仍未找到关键字和给定值相等的记录,则查找失败。
应用范围:
- 顺序表或线性链表表示的静态查找表
- 表内元素之间无序
数据元素类型定义如下:


算法描述:
 设置监视哨的顺序查找:
设置监视哨的顺序查找:
 算法分析:时间复杂度O(n)
算法分析:时间复杂度O(n)
算法优点是算法简单,对表结构无任何要求,既适用于顺序结构,也适用于链式结构,无论记录是否按关键字有序均可应用。
缺点就是平均查找长度大,查找效率较低,所以当n很大时,不宜使用顺序查找。
折半查找(二分或对分查找)
折半查找是一种效率高效的查找方法。但是折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
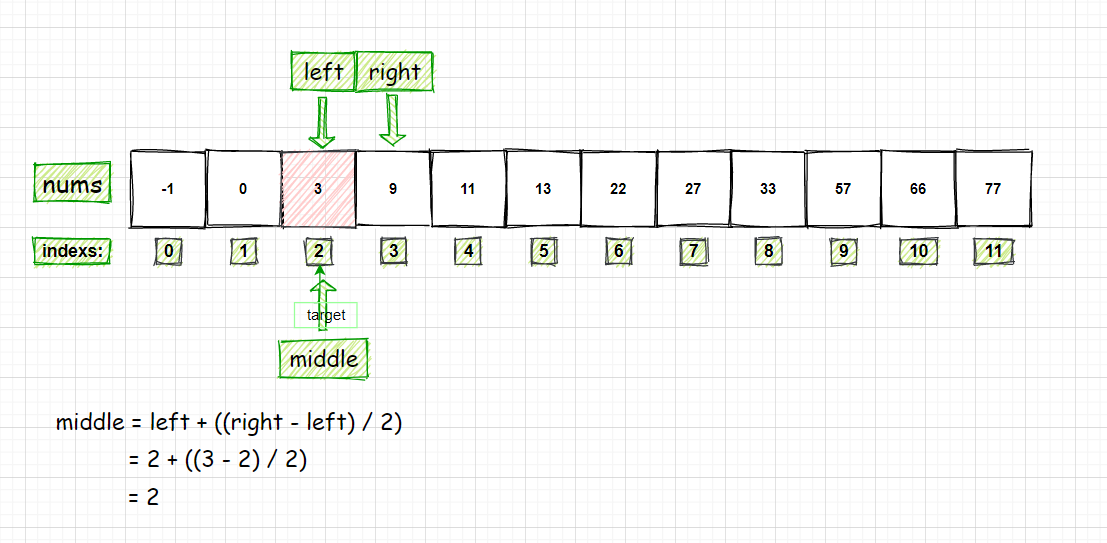
折半查找算法思路:(非递归)
- 设表长为n、low、high和mid分别指向待查元素所在区间的上界、下界和中点,key为给定的要查找的值
- 初始时,令low=1,high=n,mid=[(low+high)/2]
- 让k与mid指向的记录比较;若key==R[mid].key,查找成功;若key<R[mid].key,则high=mid-1;若key>R[mid].key,则low=mid+1;若low>high,则返回0代表元素不存在。

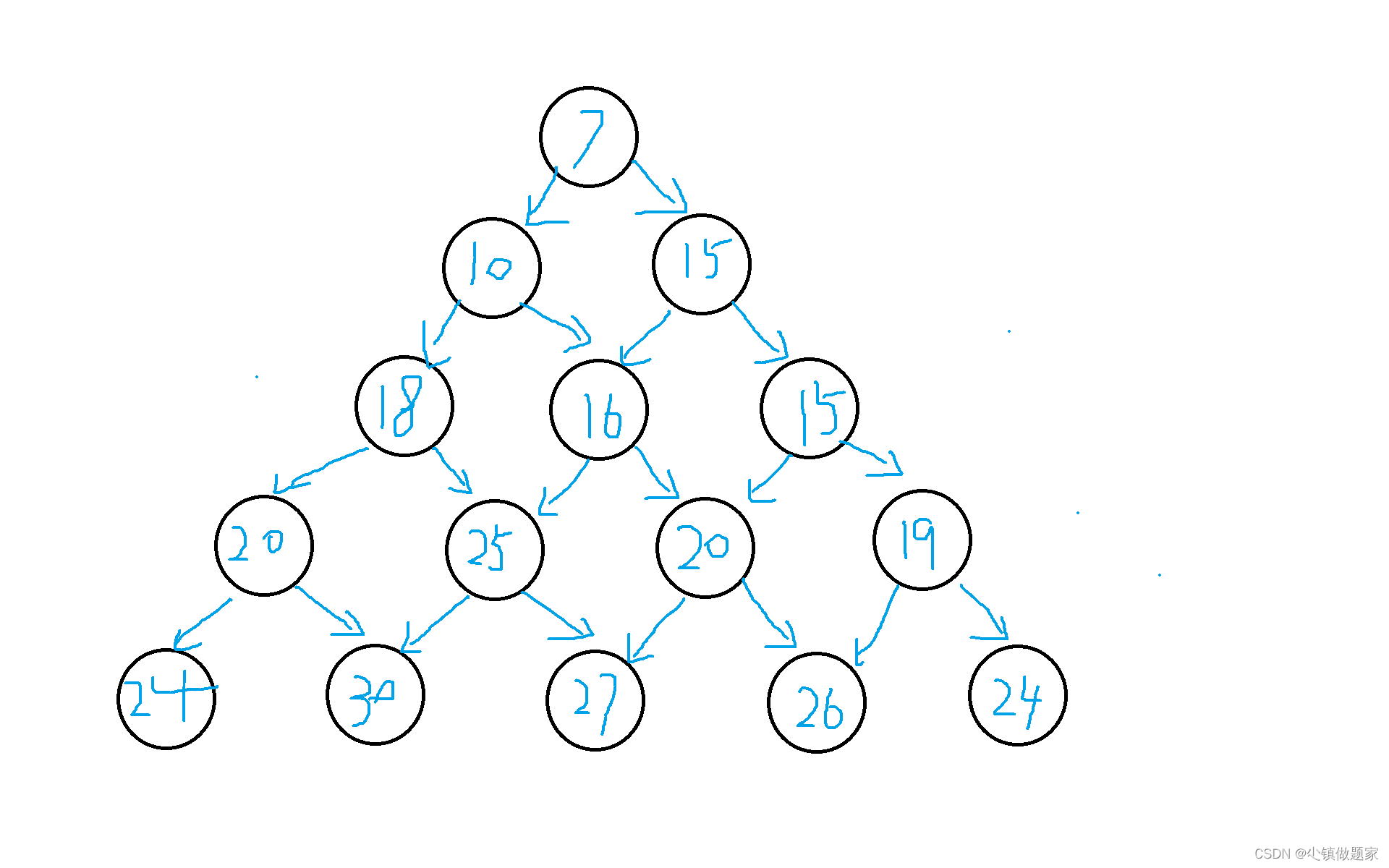
折半查找的性能分析——判定树
思路:把顺序表中的每个元素查找到所用的查找次数写出来,然后次数为1的作为树的根结点,然后查找次数为2的放到第二层,依次把每个元素放到树中。
查找成功:
比较次数=路径上的结点数
比较次数=结点的层数
比较次数是小于或等于树的深度(log2n)+1
平均查找长度ASL(成功时):

折半查找优点:效率比顺序查找高
缺点:折半查找只适用于有序表,且限于顺序存储结构(对线性链表是无效的)
分块查找(索引顺序查找)
分块查找是一种性能介于顺序查找和折半查找之间的一种查找方法。
条件:
- 将表分成几块,且表或者有序,或者分块有序;即若i<j,则第j块中所有记录的关键字均大于第i块中的最大关键字。(注意再块内元素可以是无序的)
- 建立索引表(每个结点含有最大关键字域和指向本块第一个结点的指针,且按关键字有序)
查找过程:首先确定待查记录所在块(顺序或折半查找),再再块内查找(顺序查找)
分块查找的平均查找长度:
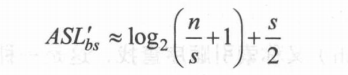
其中n为元素个数,s为每块元素个数
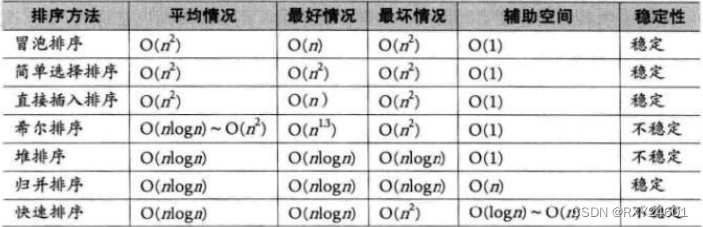
查找方法比较: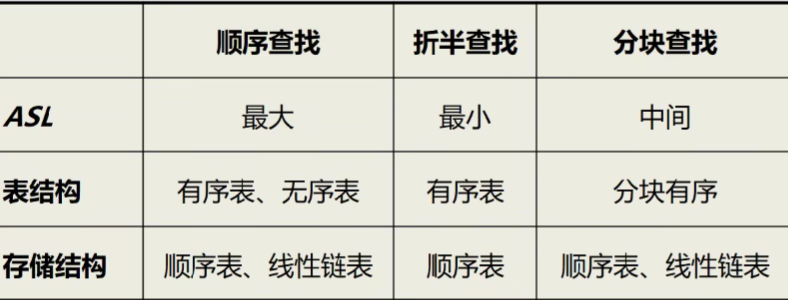
树表的查找
当表插入、删除操作频繁时,为维护表的有序性,需要移动表中很多记录。我们改用动态查找表,表结构在查找过程中动态生成。
二叉排序树
二叉排序树(Binary Sort Tree)又称二叉查找树,它是一种对排序和查找都很有用的特殊叉树。
定义:
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 它的左、右子树也分别为二叉排序树。
二叉排序树是递归定义的。由定义可以得出二叉排序树的一个重要性质:中序遍历一棵二叉树时可以得到一个结点值递增的有序序列。
二叉排序树的二叉链表存储:

二叉排序树的查找:
①若二叉排序树为空,则查找失败,返回空指针。
②若二叉排序树非空,将给定值key与根结点的关键字T->data.key进行比较:
- 若key 等于T->data.key,则查找成功,返回根结点地址;
- 若key小于T>data.key,则递归查找左子树;
- 若key大于T->data.key,则递归查找右子树。
算法分析:

二叉排序树的查找分析:含有n个结点的二叉排序树的平均查找长度和树的形态有关。
最好情况:与折半查找中的判定树相同;O(log2n)
最坏情况:变成单支树的形态O(n)
二叉排序树的插入:
算法步骤:
若二叉排序树为空,则待插入结点*S作为根结点插入到空树中。
若二叉排序树非空,则将key与根结点的关键字T->data.key 进行比较:
- 若key小于T->data.key,则将*S插入左子树;
- 若key大于T->data.key,则将*S插入右子树。
注意:新插入的结点一定是在叶子上
算法描述:

二叉排序树的创建:
①将二叉排序树T初始化为空树
②读入一个关键字为key的结点。
③如果读入的关键字key不是输人结束标志,则循环执行以下操作:
- 将此结点插入二叉排序树T中
- 读入一个关键字为key的结点
算法描述:

一个无序序列可通过构造二叉排序树而变成一个有序序列,构造树的过程就是对无序序列进行排序的过程。
插入的结点均为叶子结点,故无需移动其他结点。相当于在有序序列上插入记录而无需移动其他记录。
关键字的输入顺序不同,建立的不同二叉排序树。
二叉排序树的删除:
被删除的结点可能是二叉排序树中的任何结点,删除结点后,要根据其位置不同修改其双结点及相关结点的指针,以保持二叉排序树的特性。
从二叉排序树中删除一个结点,不能把以该结点为根的子树都删去,只能删掉该节点,并且还应保证删除后所得的二叉树仍然满足二叉排序树的性质不变。
算法步骤:
首先从二叉排序树的根结点开始查找关键字为key 的待删结点,如果树中不存在此结点,则不做任何操作;否则,假设被删结点为*p(指向结点的指针为p),其双亲结点为*f(指向结点的指针为f),PL和PR分别表示其左子树和右子树。
(1)若*p结点为叶子结点,即PL和PR均为空树。由于删去叶子结点不破坏整棵树的结构,则只需修改其双亲结点的指针即可。f->lchild= NULL
(2)若*p结点只有左子树PL或者只有右子树PR,此时只要令PL或PR直接成为其双亲结点*f的左子树即可。f->lchild= p->lchild;(或f->lchild= p->rchild;)
(3)若*p结点的左子树和右子树均不空。则让其左子树的最大值替换p结点,然后删除其左子树的最大值;或者取其右子树的最小值,然后让右子树的最小点替换p结点,然后删除其右子树的最小值。
平衡二叉树
二叉排序树查找算法的性能取决于二叉树的结构,而二叉排序树的形状则取决于其数据集。树的高度越小,查找速度越快;希望二叉树的高度可能小,因此我们研究一种特殊类型的二叉排序树,称为平衡二叉树(AVL)
平衡二叉树或者是空树,或者是具有如下特征的二叉排序树:
(1)左子树和右子树的深度之差的绝对值不超过1;
(2)左子树和右子树也是平衡二叉树
平衡因子:该节点左子树和右子树的深度之差。
平衡二叉树必须保证每个结点都是平衡因子绝对值小于1
对于一棵有n个结点的AVL树,其高度保持在O(log2n)数量级,ASL也保持在O(log2n)量级
平衡调整的4种方法:

调整原则:降低高度 保持二叉排序树性质
注意:要是添加一个元素之后出现多个平衡因子绝对值大于1,那么选择子树小的进行调整
判断失衡类型:就是找到那个平衡因子绝对值大于1的结点,然后以这个结点为起点,向后看
B-树
前面介绍的查找方法均适用于存储计算机内存中较小的文件,统称为内查找法,都是以结点为单位进行查找。对于文件大且存放于外存进行查找时要用外查找;下面讲述用于外查找的平衡二叉树——B-树。
定义:
一棵m阶的B-树,或为空树,或为满足下列特性的m叉树:
(1)树中每个结点至多有m棵子树;
(2)若根结点不是叶子结点,则至少有两棵子树;
(3)除根之外的所有非终端结点至少有m/2棵子树;
(4)所有的叶子结点都出现在同一层次上,并且不带信息,通常称为失败结点(失败结点并不存在,指向这些结点的指针为空。引入失败结点是为了便于分析B-树的查找性能);
(5)所有的非终端结点最多有m-1个关键字
B-树特点:
- 所有叶子结点均在同一层次,这体现出其平衡的特点。
- 树中每个结点中的关键字都是有序的,且关键字K1"左子树"中的关键字均小于K1,而其”右子树“中的关键字均大于K1,这体现出其有序的特点。
- 除叶子结点外,其余结点最多有m-1个关键字,m棵子树
B-树的查找:

B+树
B+树是一种B-树的变形,更适用于文件索引系统。
B+树和B-树的差异:
-棵m阶的B+树和m阶的B-树的差异在于:
(1)有n棵子树的结点中含有n个关键字;
(2)所有的叶子结点中包含了全部关键字的信息,以及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接;
(3)所有的非终端结点可以看成是索引部分,结点中仅含有其子树(根结点)中的最大(或最小)关键字
散列表的查找
散列表的基本概念
前面讨论的线性表、树表结构的查找方法,这类查找方法都是以关键字的比较为基础的。而散列表的思想是通过对元素的关键字值进行某种运算,直接求出元素的地址,即使用关键字到地址的直接转换方法,而不需要反复比较。
散列函数和散列地址:在记录的存储位置p和其关键字key之间建立一个确定的对应的关系H,使p=H(key),称这个对应关系H为散列函数,p为散列地址。
散列方法(杂凑法):选取某个函数,依该函数按关键字计算元素的存储位置,并按此存放;查找时,由同一个函数对给定值k计算地址,将k与地址单元中元素关键码进行比对,确定查找是否成功。
散列表:一个有限连续的地址空间,用以存储按散列函数计算得到相应散列地址的数据记录。通常散列表的存储空间是一个一维数组,散列地址是数组的下标。
冲突和同义词:对不同的关键字可能得到同一散列地址,即key1!=key2,而H(key1)=H(key2),这种现象称为冲突。具有相同函数值的关键对该散列函数来说称作同义词,key1与key2互称为同义词。(冲突是不可避免的,我们只能尽可能减少)
散列函数的构造方法
使用散列表要解决好两个问题:
- 构造好的散列函数,所选函数尽可能简单,以便提高转换速度。所选函数对关键码计算出的地址,应在散列地址集中致均匀分布,以减少空间浪费。
- 制定一个好的解决冲突的方案,查找时如果从散列函数计算出的地址查不到关键码,则应当依据解决冲突的规则,有规律的查询其它相关单元。
构造散列函数要考虑一下因素:
- 散列表的长度
- 关键字的长度
- 关键字的分布情况
- 计算散列函数所需的时间
- 记录的查找频率
构造方法:
- 除留余数法
- 折叠法
- 平方取中法
- 数字分析法
处理冲突的方法:
- 开放地址法:基本思想就是把记录都存储在散列表数组中,当某一记录关键字key的初始散列地址发生冲突时,以冲突地址为基础,采用某种办法计算得到另外一个地址,如果仍重复依旧按照此方法继续寻找;找下一个地址的过程称为探测。
- 线性探测法:发生冲突时,从冲突地址的下一单元顺序寻找空单元,如果到最后一个位置也没有找到空单元,则回到表头位置开始继续寻找,直到寻找到一个空位。如果找不到空位,说明表已经满了,需要进行溢出处理
- 二次探测法:

2.链地址法:基本思想就是把具有相同散列地址的记录放在同一个单链表中,称之为同义词链表。有m个散列地址就有m个单链表,同时用数组HT[0……m-1]存放各个链表的头指针,凡是散列地址为i的记录都以结点方式插入到以HT[i]为头节点的单链表中。
优点:
- 非同义词不会冲突,无”聚焦“现象
- 链表上结点空间动态申请,更适合于表长不确定的情况
开放地址和链地址法的比较:
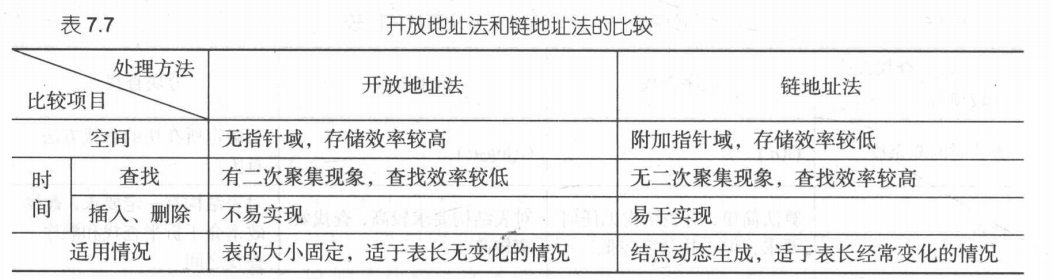
散列表的查找
算法步骤:
- 给定待查找的关键字key,根据造表时设定的散列函数计算H0= H(key)
- 若单元H0为空,则所查元素不存在。
- 若单元H0中元素的关键字为 key,则查找成功。
- 否则重复下述解决冲突的过程:
- 按处理冲突的方法,计算下一个散列地址H
- 若单元H为空,则所查元素不存在;
- 若单元H中元素的关键字为key,则查找成功。
算法描述:

查找过程中需要和给定值进行比较的关键字的个数取决于三个因素:散列函数、处理冲突的方法、散列表的装填因子a(装填因子a=表中填入的记录数/散列表的长度) ;a标志散列表的装满程度。直观的看,a越小,发生冲突的可能性越小;反之,a越大,表中已填入的记录越多,再做记录时,发生冲突的可能性越大,则查找时给定值与之进行比较的关键字的个数也就越多。
散列函数的好坏首先影响出现冲突的频繁程度。

结论:
- 散列表技术具有很好的平均性能,优于一些传统的技术
- 链地址法优于开地址法
- 除留余数法作散列函数优于其它类型函数




![[附源码]Node.js计算机毕业设计关山社区居民信息管理系统Express](https://img-blog.csdnimg.cn/11150f545f4343a9948416460c81dff7.png)