目录
一 算法简介
1)算法解释
2)前提
3)思想
4)分类
5)算法模板
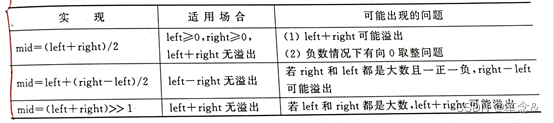
mid的计算的实现方法
二分法模板
求某个数的平方根:
二 算法实践
1)问题引入
2)问题解答
1)解法一:左闭右闭
思想:
代码:
模拟过程:
2)解法二:左闭右开
思想:
代码:
模拟过程
三 实数二分
算法模板
一 算法简介
1)算法解释
二分查找也常被称为二分法或者折半查找,每次查找时通过将待查找区间分成两部分并只取 一部分继续查找,将查找的复杂度大大减少。对于一个长度为 O(n) 的数组,二分查找的时间复 杂度为 O(log n)。
举例来说,给定一个排好序的数组 {3,4,5,6,7},我们希望查找 4 在不在这个数组内。第一次 折半时考虑中位数 5,因为 5 大于 4, 所以如果 4 存在于这个数组,那么其必定存在于 5 左边这一 半。于是我们的查找区间变成了 {3,4,5}。(注意,根据具体情况和您的刷题习惯,这里的 5 可以 保留也可以不保留,并不影响时间复杂度的级别。)第二次折半时考虑新的中位数 4,正好是我们 需要查找的数字。于是我们发现,对于一个长度为 5 的数组,我们只进行了 2 次查找。如果是遍 历数组,最坏的情况则需要查找 5 次。
我们也可以用更加数学的方式定义二分查找。给定一个在 [a, b] 区间内的单调函数 f (x),若 f (a) 和 f (b) 正负性相反,那么必定存在一个解 c,使得 f (c) = 0。在上个例子中,f (x) 是离散函数 f (x) = x +2,查找 4 是否存在等价于求 f (x) −4 = 0 是否有离散解。因为 f (1) −4 = 3−4 = −1 < 0、 f (5) − 4 = 7 − 4 = 3 > 0,且函数在区间内单调递增,因此我们可以利用二分查找求解。如果最后 二分到了不能再分的情况,如只剩一个数字,且剩余区间里不存在满足条件的解,则说明不存在 离散解,即 4 不在这个数组内。
具体到代码上,二分查找时区间的左右端取开区间还是闭区间在绝大多数时候都可以,因此 有些初学者会容易搞不清楚如何定义区间开闭性。这里我提供两个小诀窍,第一是尝试熟练使用 一种写法,比如左闭右开(满足 C++、Python 等语言的习惯)或左闭右闭(便于处理边界条件), 尽量只保持这一种写法;第二是在刷题时思考如果最后区间只剩下一个数或者两个数,自己的写 法是否会陷入死循环,如果某种写法无法跳出死循环,则考虑尝试另一种写法。 二分查找也可以看作双指针的一种特殊情况,但我们一般会将二者区分。双指针类型的题, 指针通常是一步一步移动的,而在二分查找里,指针每次移动半个区间长度。
2)前提
1)序列为有序序列
2)序列中没有重复元素:因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的
3)查找的数量只能是一个,而不是多个
3)思想
因为整个数组是有序的,数组默认是递增的。
1)首先选择数组中间的数字和需要查找的目标值比较
2)如果相等最好,就可以直接返回答案了
3)如果不相等
如果中间的数字大于目标值,则中间数字向右的所有数字都大于目标值,全部排除
如果中间的数字小于目标值,则中间数字向左的所有数字都小于目标值,全部排除
提示:不用去纠结数组的长度是奇数或者偶数的时候,怎么取长度的一半
这种情况并不影响我们对中间数字和目标数字大小关系的判断
- 只要中间数字大于目标数字,就排除右边的
- 只要中间数字小于目标数字,就排除左边的
真正影响的是中间那个数字到底该不该加入下一次的查找中,也就是边界问题
4)分类
二分查找涉及的很多的边界条件,逻辑比较简单,但就是写不好。例如到底是 while(left < right) 还是 while(left <= right),到底是right = middle呢,还是要right = middle - 1呢?
容易搞混淆;主要是因为对区间的定义没有想清楚,区间的定义就是不变量。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是循环不变量规则。
写二分法,区间的定义一般为两种:
1)左闭右闭即[left, right](便于处理边界条件)
2)左闭右开即[left, right)。
5)算法模板
提示:>>等同于除以二
拓展:/2和>>1的区别:
1.操作对象类型不同
>>是右移符百号,它在操作时只允许整数
/是除法,它可以操作不同类型的数据:浮点数除法最终结果是浮点数,整数除法的最终结果是整数。
只有当被操作数数据类型为知大于0的整数时,运算的结果才是相同的。
2.运算效率不同
右移操作通常情况下,会比整数除法速度快。涉及到浮点数的除法速度是最慢的。
3.优先级不同
右移运算的优先级比除法低,在同时参与的运算中,先计算乘除,后计算左移或右移
mid的计算的实现方法
二分法模板
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}求某个数的平方根:
#include<stdio.h>
int main(){
double x;
scanf("%lf",&x);
double l = 0, r = x;
while(r - l > 1e-8){
double mid = (l + r) / 2;
if(mid * mid >= x) r = mid;
else l = mid;
}
printf("%lf\n",l);
return 0;
}二 算法实践
1)问题引入
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
2)问题解答
1)解法一:左闭右闭
思想:
我们定义 target 是在一个在左闭右闭的区间里,也就是[left, right]
因为定义target在[left, right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:
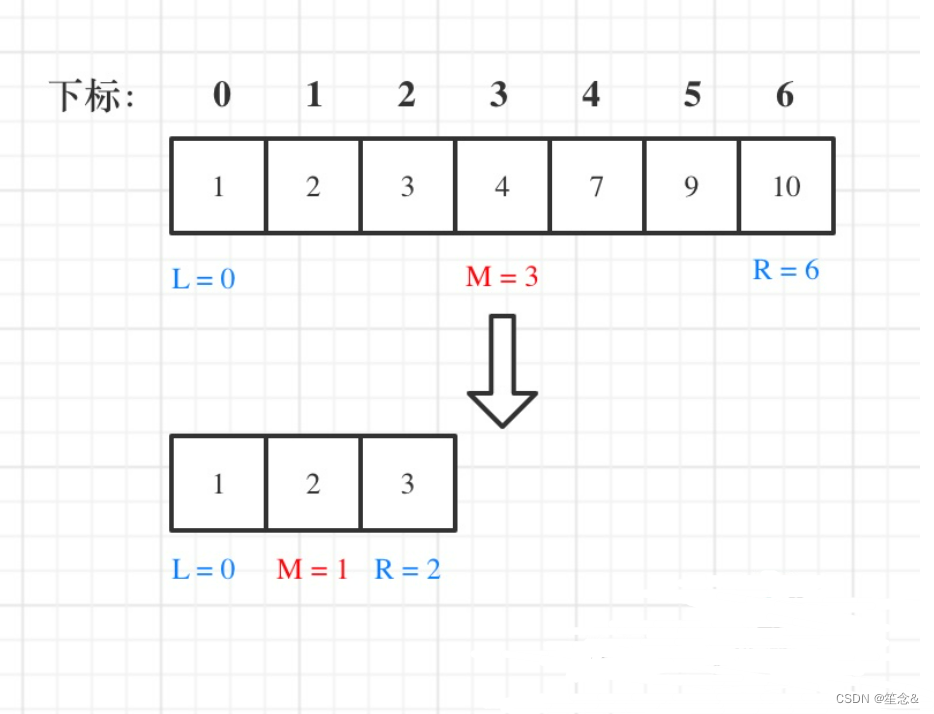
代码:
// (版本一) 左闭右闭区间 [left, right]
int search(int* nums, int numsSize, int target){
int left = 0;
int right = numsSize-1;
int middle = 0;
//若left小于等于right,说明区间中元素不为0
while(left<=right) {
//更新查找下标middle的值
middle = (left+right)/2;
//此时target可能会在[left,middle-1]区间中
if(nums[middle] > target) {
right = middle-1;
}
//此时target可能会在[middle+1,right]区间中
else if(nums[middle] < target) {
left = middle+1;
}
//当前下标元素等于target值时,返回middle
else if(nums[middle] == target){
return middle;
}
}
//若未找到target元素,返回-1
return -1;
}模拟过程:
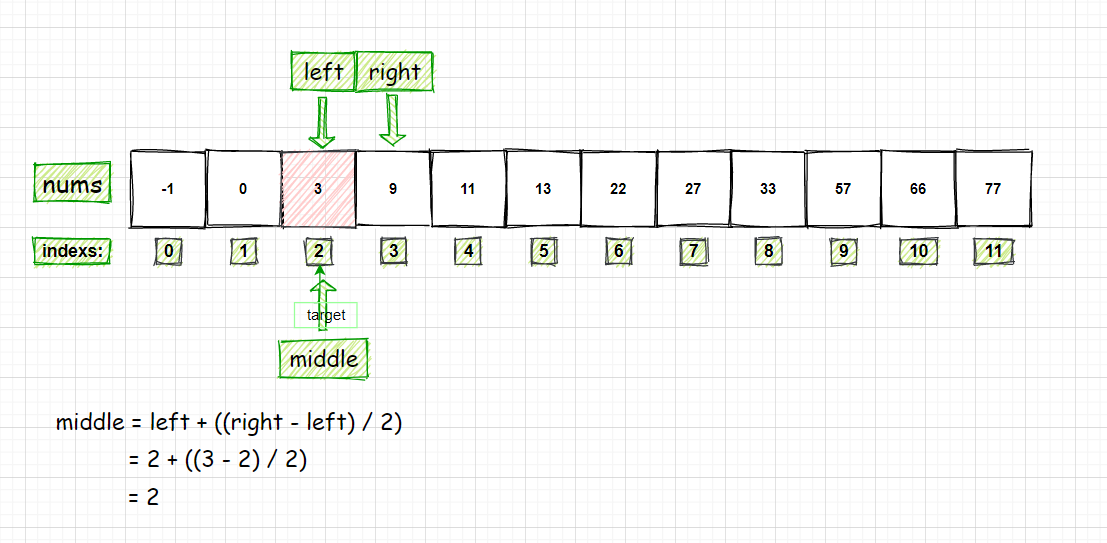
首先看一个数组,需要对这个数组进行操作。需要对33进行查找的操作,那么target 的值就是33
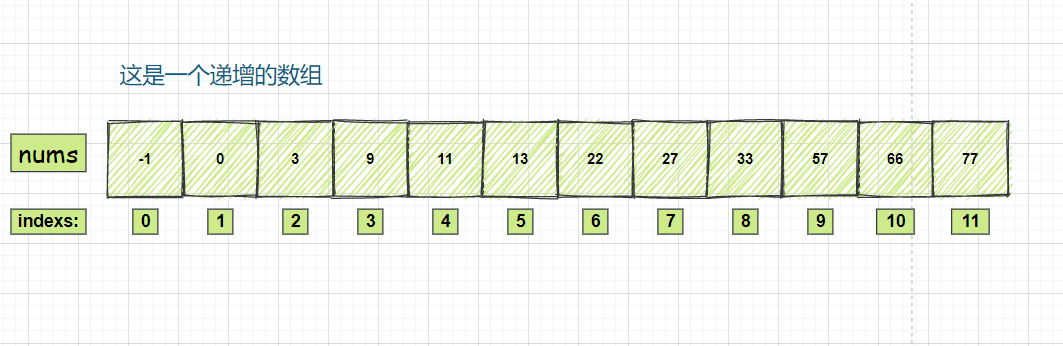
首先,对 left 的值和 right 的值进行初始化,然后计算 middle 的值
left = 0, right = size - 1middle = (left + (right - left) / 2 )
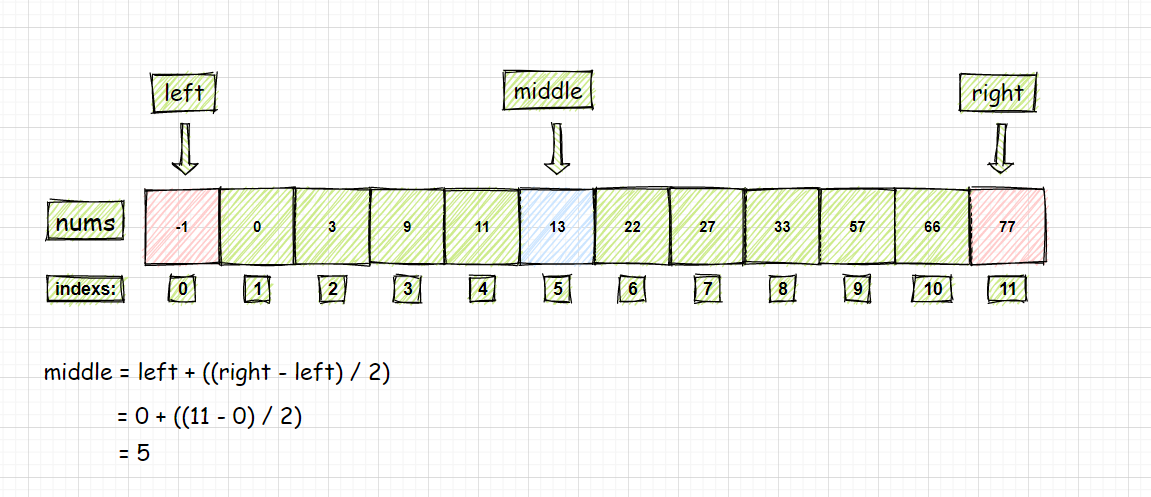
比较 nums[middle] 的值和 target 的值大小关系
if (nums[middle] > target),代表middle向右所有的数字大于target
if (nums[middle] < target),代表middle向左所有的数字小于target
既不大于也不小于就是找到了相等的值
nums[middle] = 13 < target = 33,left = middle + 1
如下图:
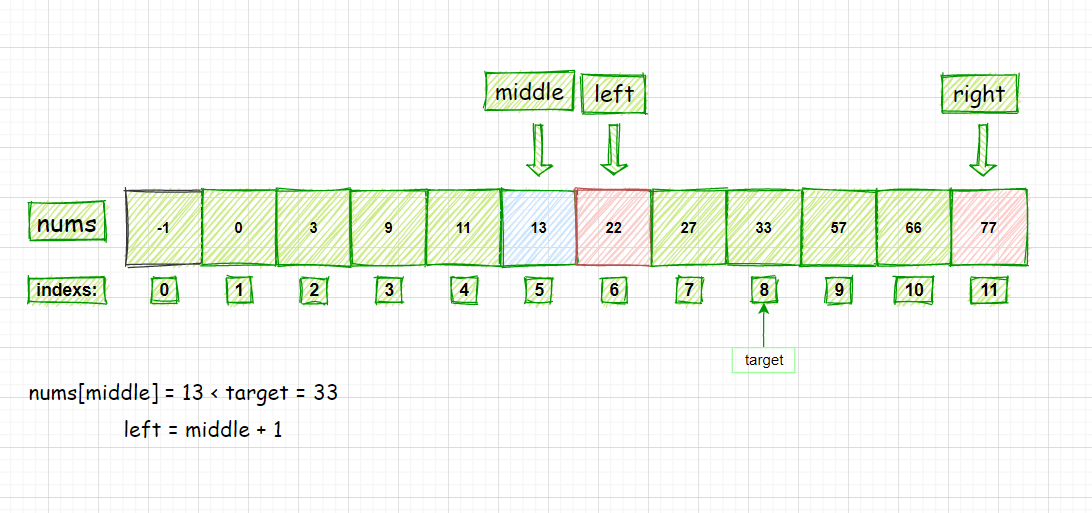
-
循环条件为
while (left <= right) -
此时,
left = 6 <= right = 11,则继续进行循环 -
当前,
middle = left + ((right - left) / 2),计算出 middle 的值
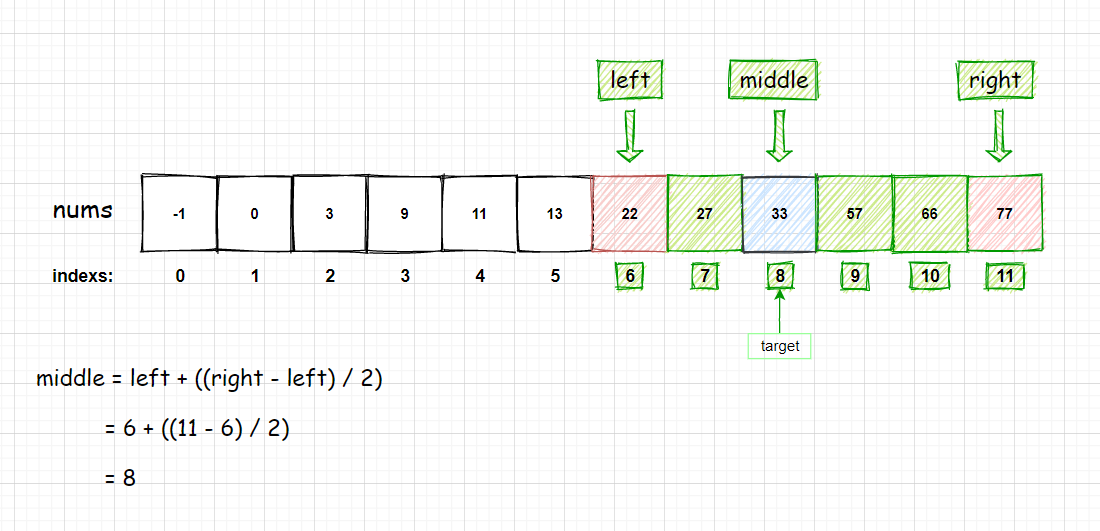
计算出 middle 的值后,比较 nums[middle] 和 target 的值,发现:
- nums[middle] = 33 == target = 33,找到目标
2)解法二:左闭右开
思想:
定义 target 是在一个在左闭右开的区间里,也就是[left, right)
有如下两点:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(注意和方法一的区别)
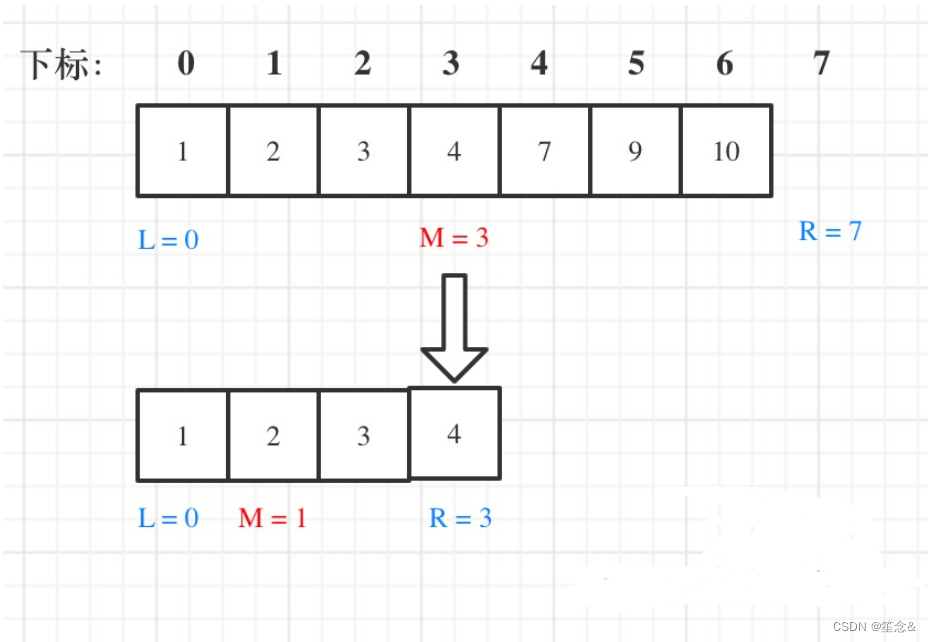
代码:
// (版本二) 左闭右开区间 [left, right)
int search(int* nums, int numsSize, int target){
int length = numsSize;//注意不是numsize-1,因为此时是左闭右开【0,n】
int left = 0;
int right = length; //定义target在左闭右开的区间里,即:[left, right)
int middle = 0;
while(left < right){ // left == right时,区间[left, right)属于空集,所以用 < 避免该情况
int middle = left + (right - left) / 2;
if(nums[middle] < target){
//target位于(middle , right) 中为保证集合区间的左闭右开性,可等价为[middle + 1,right)
left = middle + 1;
}else if(nums[middle] > target){
//target位于[left, middle)中
right = middle ;
}else{ // nums[middle] == target ,找到目标值target
return middle;
}
}
//未找到目标值,返回-1
return -1;
}模拟过程
- 需要查找的值为3
第一步是初始化 left 和 right 的值,然后计算 middle 的值
- left = 0, right = size
- 循环条件while (left < right)
因为是左闭右开区间,所以数组定义如下:
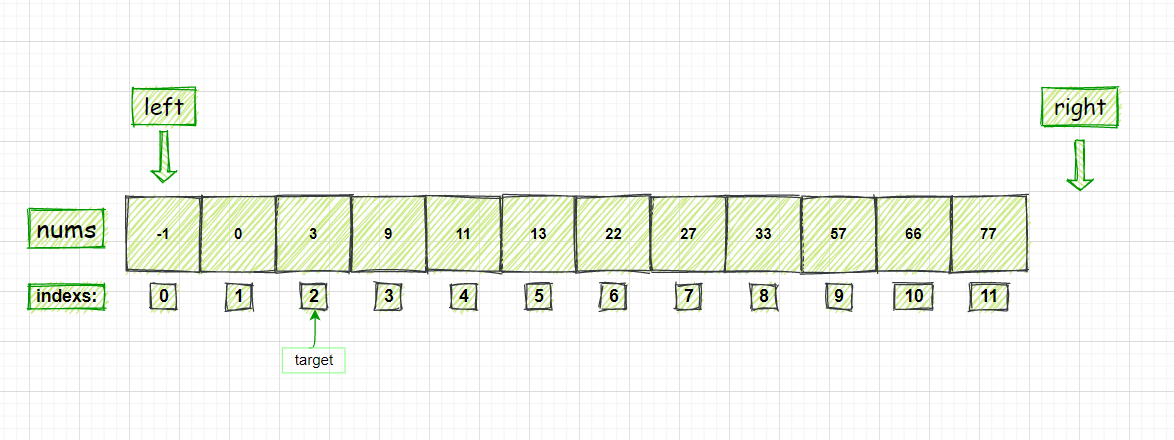
- 计算 middle 的值
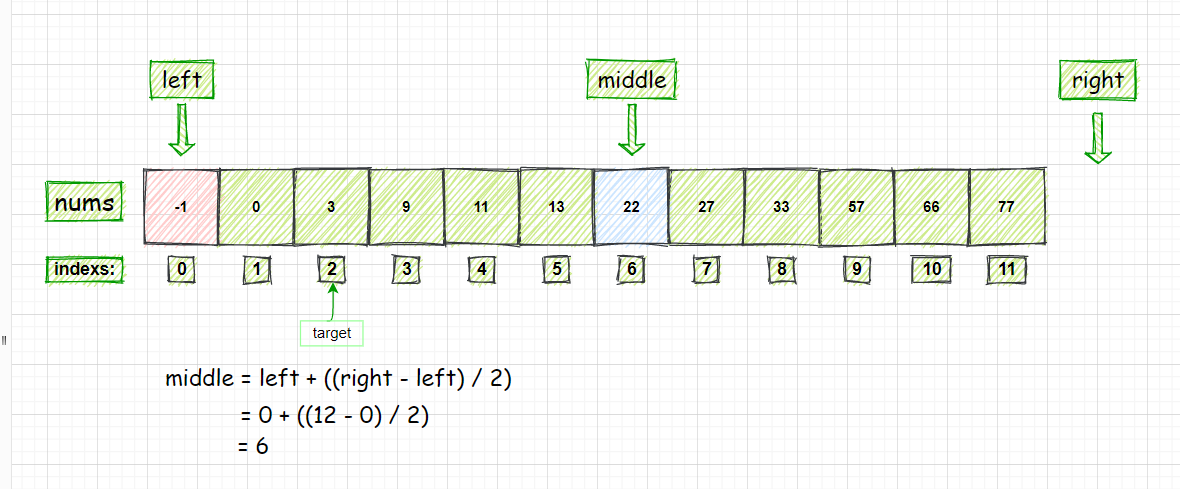
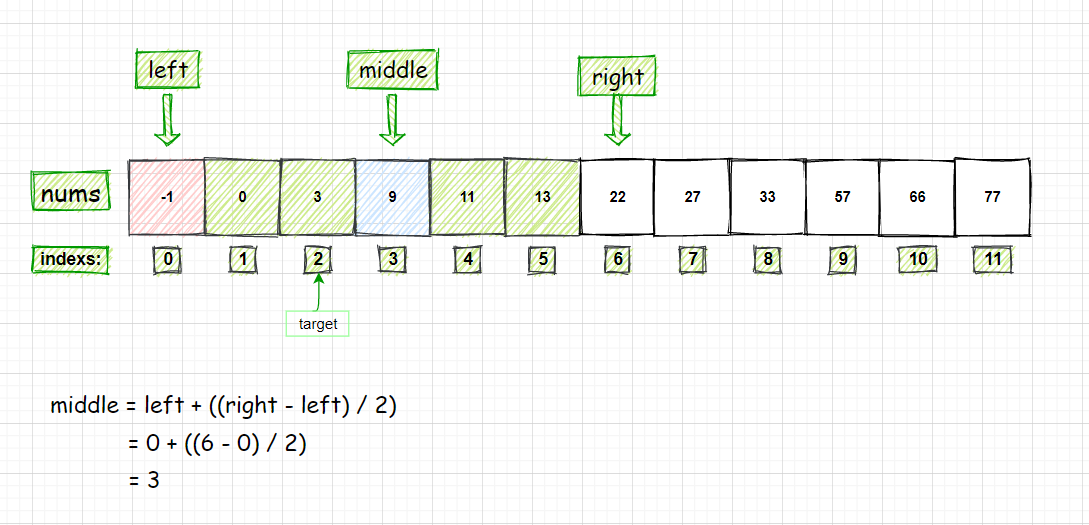
- 比较 nums[middle] 和 target 的大小:因为 nums[middle] = 22 > target = 3
- 所以 right = middle
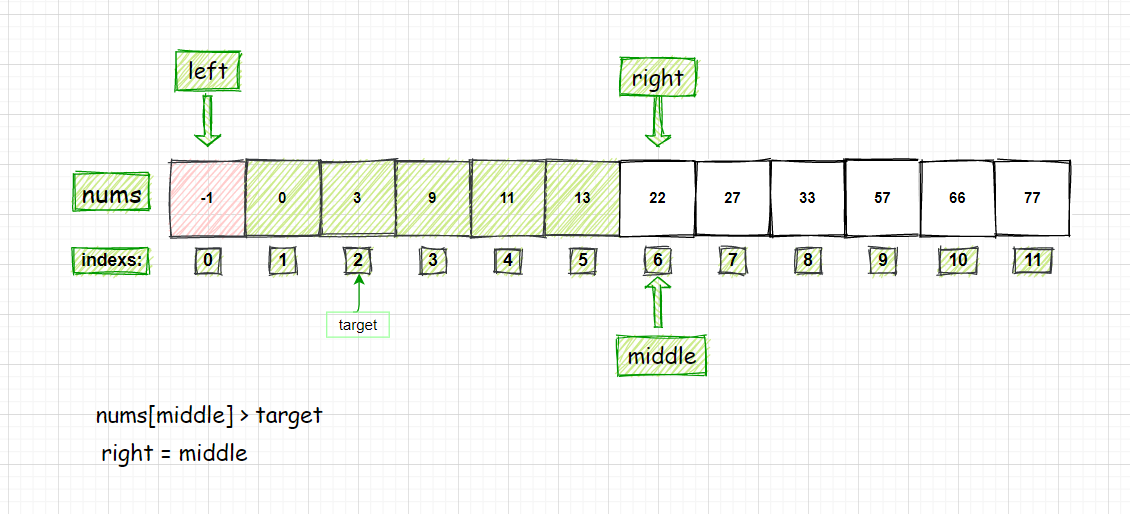
- 符合循环的条件,接着计算 middle 的值
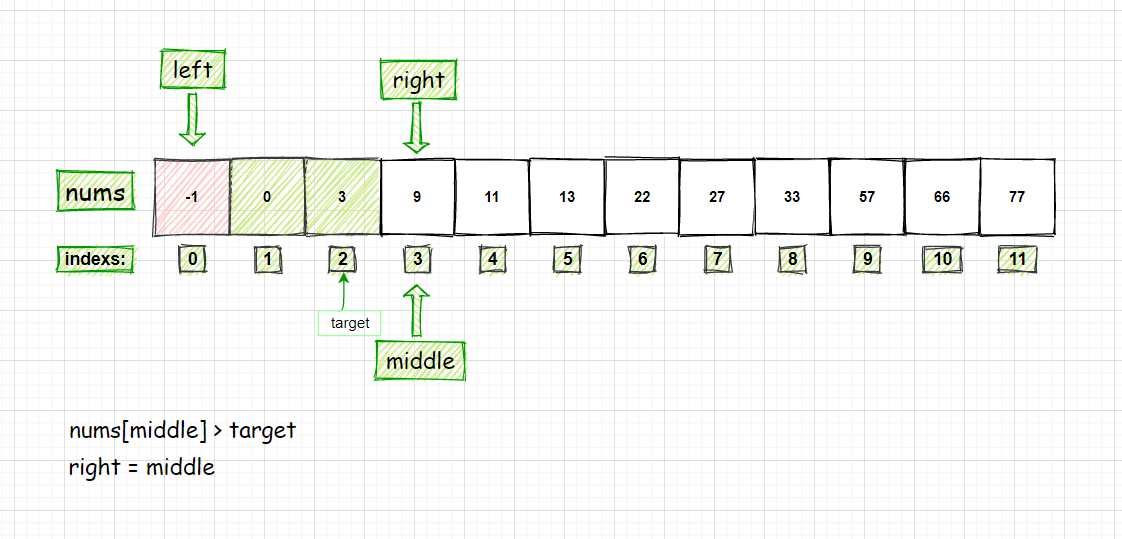
- 比较 nums[middle] 和 target 的大小:因为 nums[middle] = 9 > target = 3
- 所以 right = middle
- 符合循环的条件,继续计算 middle 的值
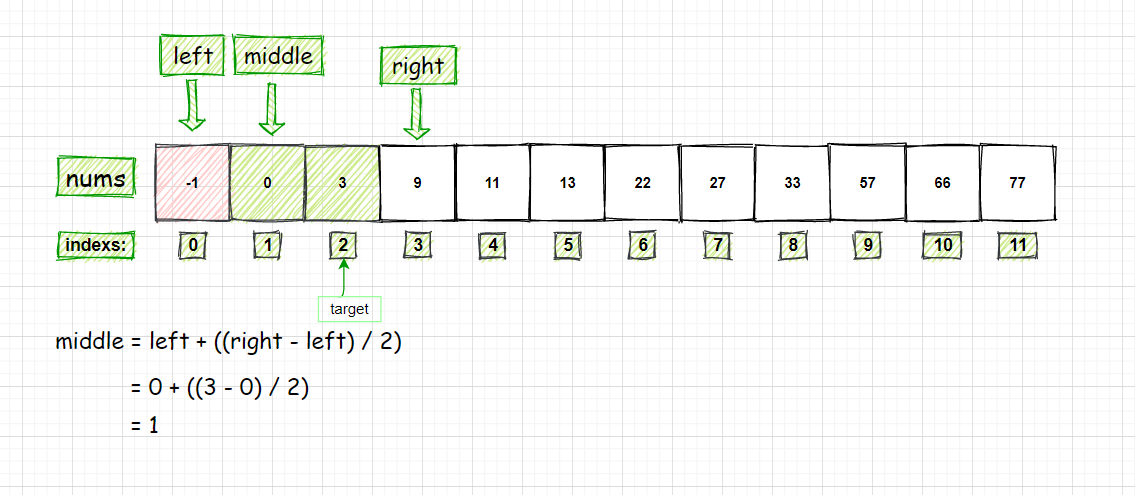
- 比较 nums[middle] 和 target 的大小关系:因为nums[middle] = 0 < target = 3
- 所以 left = middle + 1
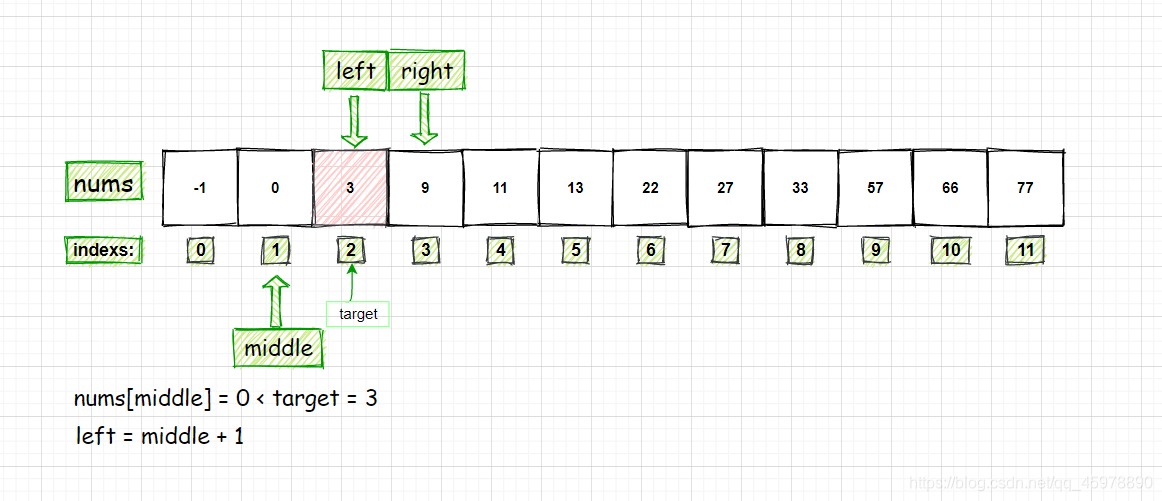
- 符合循环条件,接着计算 middle 的值
- 比较 nums[middle] 和 target 的关系:nums[middle] = 3 == target = 3
- 成功找到 target
3)题目练习:进击的牛战士
题目描述
在一条很长的直线上,指定n个坐标点(x1.x 2...xn)有c头牛,安排每头牛站在其中一个点(牛棚)上,这些牛战士喜欢打贾,所以尽量距离远一些,求相邻的两头牛之间距离的最大值。
## 输入格式
第一行输入两个用空格隔开的数字n和c;
第 2$ ~ N+1 行:每行一个整数,表示每个隔间的坐标。
## 输出格式
输出只有一行,即相邻两头牛最大的最近距离。
## 样例 #1
### 样例输入 #1
5 3
1
2
8
4
9
### 样例输出 #1
3
数据范围:2《=1000000,0《=xi《=1000000000;
思路
1)暴力法:从小到大枚举最小距离值dis,然后检查,如果发现有一次不符合条件,那么上次枚举的就是最大值。如何检查呢?贪心法:第一头牛放在x1,第二头牛放在x2>=x1+dis的点x2,第三头牛放在x3>=x2+dis的点x3,以此类推。如果在当前最小距离下不能放c头牛,那么这个dis指就不可取。复杂度为O(nc);
2)二分法:分析从小到大检查dis的过程,发现可以用二分法寻找这个dis值。这个dis值附和二分法:他又上下边界且是单调递增的。复杂度为O(n log2n);
代码
#include <stdio.h>
#include <stdlib.h>
int cmp(const void *a,const void *b)
{
return *(int *)a> *(int *)b;
}
int n,c,i,x[100005];//牛棚数量,牛数量,牛棚坐标
int check(int dis)//当牛的距离最小为dis时,检查牛棚够不够
{
int cnt=1,place=0,i;//第一头牛,放在第一个牛棚
for(i=1;i<n;i++)//检查后面的每个牛棚
if(x[i]-x[place]>=dis)//如果距离dis的位置有牛棚
{
cnt++;//又放了一头牛
place=i;//更新上一头牛的位置
}
if(cnt>=c) return 1;//牛棚够
else return 0;
}
int main()
{
int i;
scanf("%d %d",&n,&c);
for(i=0;i<n;i++)
scanf("%d",&x[i]);
qsort(x,n,sizeof(x[1]),cmp);//对牛棚的坐标排序
int left=0,right=x[n-1]-x[0];
int ans=0;
while(left<right)
{
int mid=left+(right-left)/2;//二分
if(check(mid))
{
ans=mid;//牛棚够,先记录mid
left=mid+1;//扩大距离
}
else right=mid;//牛棚不够,缩小距离
}
printf("%d",ans);
return 0;
}三 实数二分
实数域上的二分,因为没有整数二分的取整问题,编码比整数二分简单。而实数二分与整数二分最大的区别就是精度问题。
算法模板
const double eps=1e-7;//精度,如果下面用for,可以不要eps
while(right-left>eps)//for(int i=0;i<100 ;i++)
{
double mid=left+(righ-left)/2;
if(check(mid))
right=mid;//判定然后继续二分
else
left=mid;
} 其中,循环用两种方法都可以:while(right-left>eps)或者for(int i=0;i<100 ;i++)
如果用for循环,在循环内做二分,执行100次相当于实现了1/2的100次方约等于1/10的30次方的精度,完全够用,比eps更精确。
但是,两种方法都有精度控制问题
1)for循环的循环次数不能太大或太小,一般用100次,通常比while的循环次数要多,大多数情况下,增加的时间是可以接受的。不过有些题目的逻辑比较复杂,一次for循环内部的计算量很大。那么较大的for循环次数会超时,此时应该减少到50次甚至更少,但是过少的循环次数可能导致精度不够,输出答案错误;
2)while循环同样需要仔细设计精度eps,过小的eps会超时,过大的eps会输出错误答案;
![[附源码]Node.js计算机毕业设计关山社区居民信息管理系统Express](https://img-blog.csdnimg.cn/11150f545f4343a9948416460c81dff7.png)