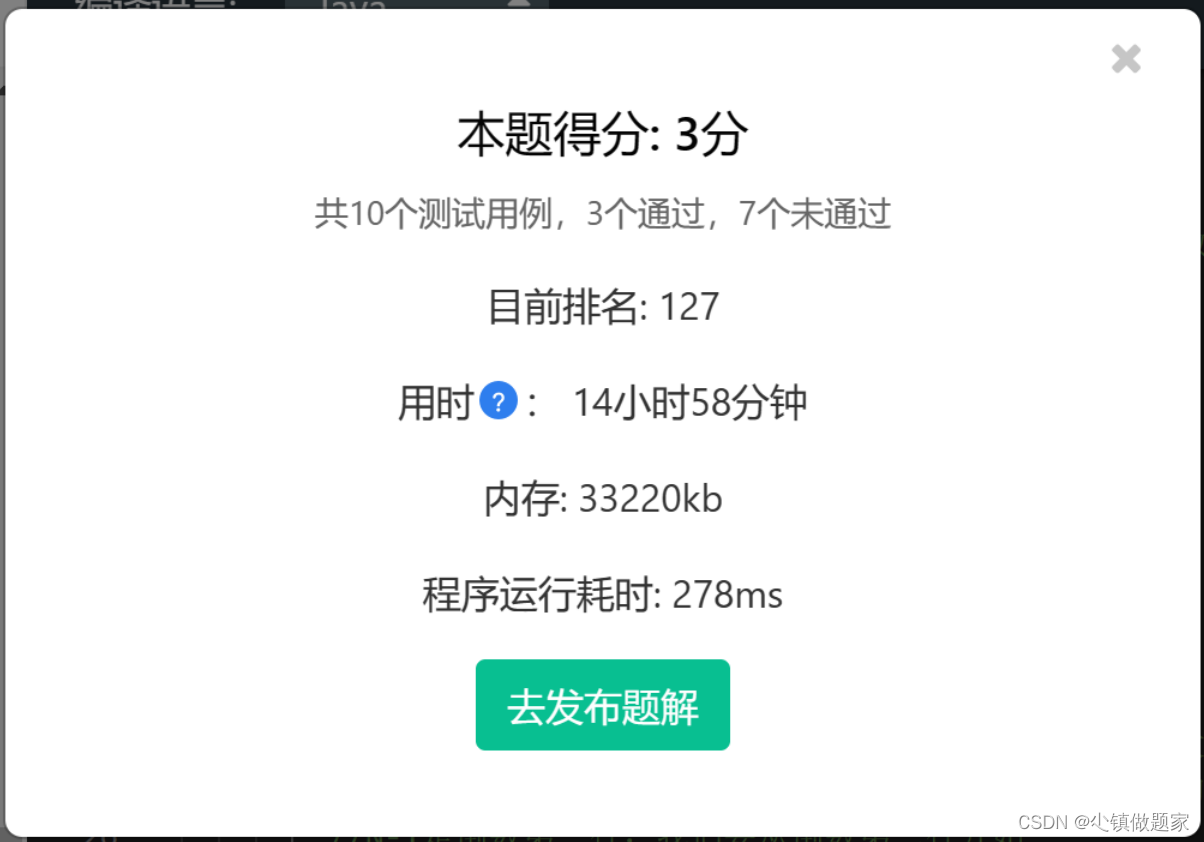
目录

题目描述

输入描述

输出描述

输入输出样例

输入

输出

思路：

AC代码（Java）：

---

题目描述

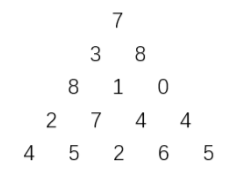
         上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

        路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。

        此外，向左下走的次数与向右下走的次数相差不能超过 1。

输入描述

        输入的第一行包含一个整数 N (1≤N≤100)，表示三角形的行数。

        下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。

输出描述

输出一个整数，表示答案。

输入输出样例

输入

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

输出

27

思路：

        一开始我以为是简单的求最大路径和，啪的一下状态转移方程就出来了，直接从下往上，从倒数第二层往上累加，dp[i][j] += Math.max( dp[i+1][j] , dp[i+1][j+1])。

        啪的一下打印dp[0][0],很快啊，就拿了3分。

         

        看到3分还愣了一下，才反应回去看题目，注意看红色标注的部分！！！那里是这道题的关键。 

        我们先假设一个N=5的三角形

        

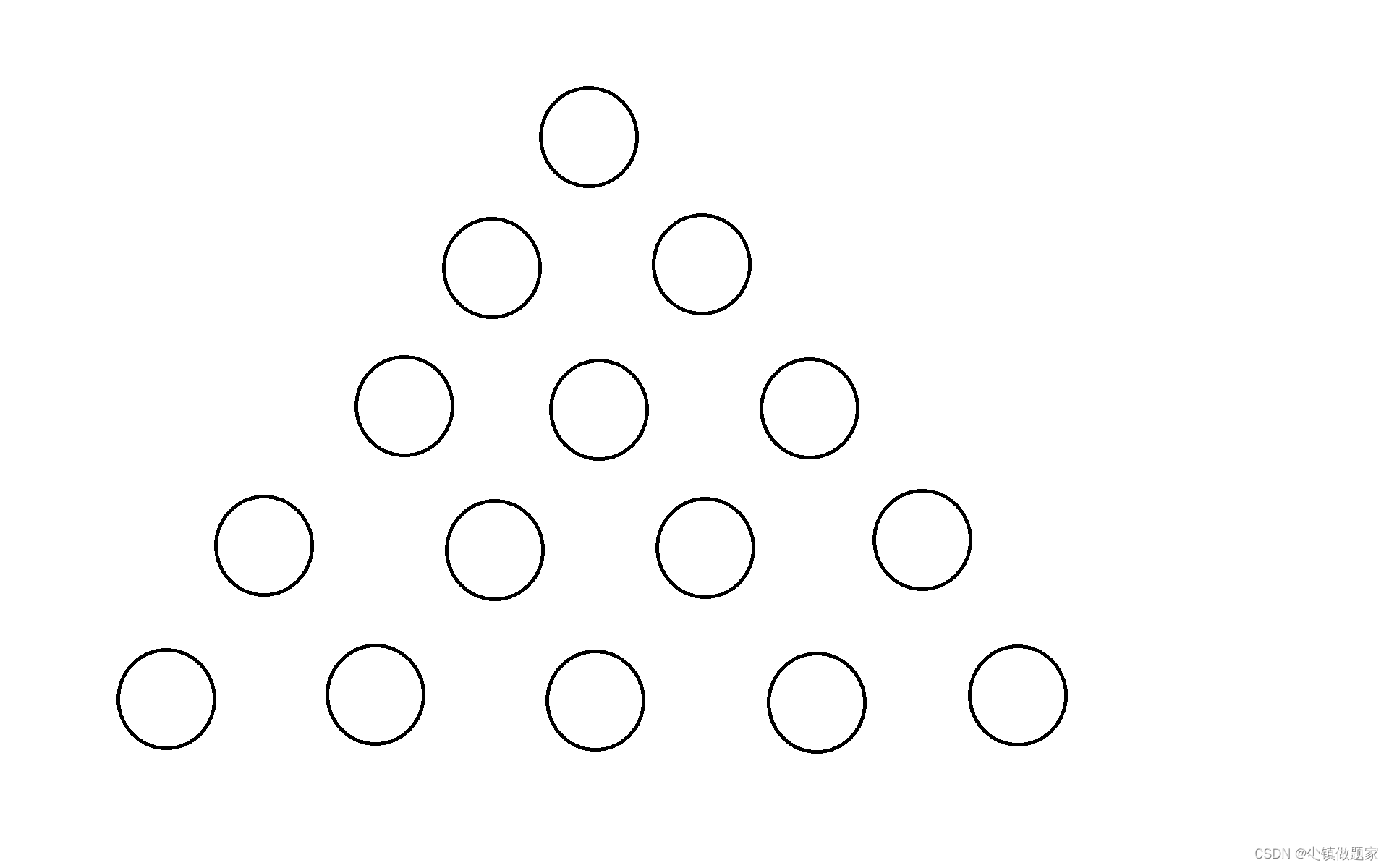
向左下，或者向右下走的话，先看第一行：

 

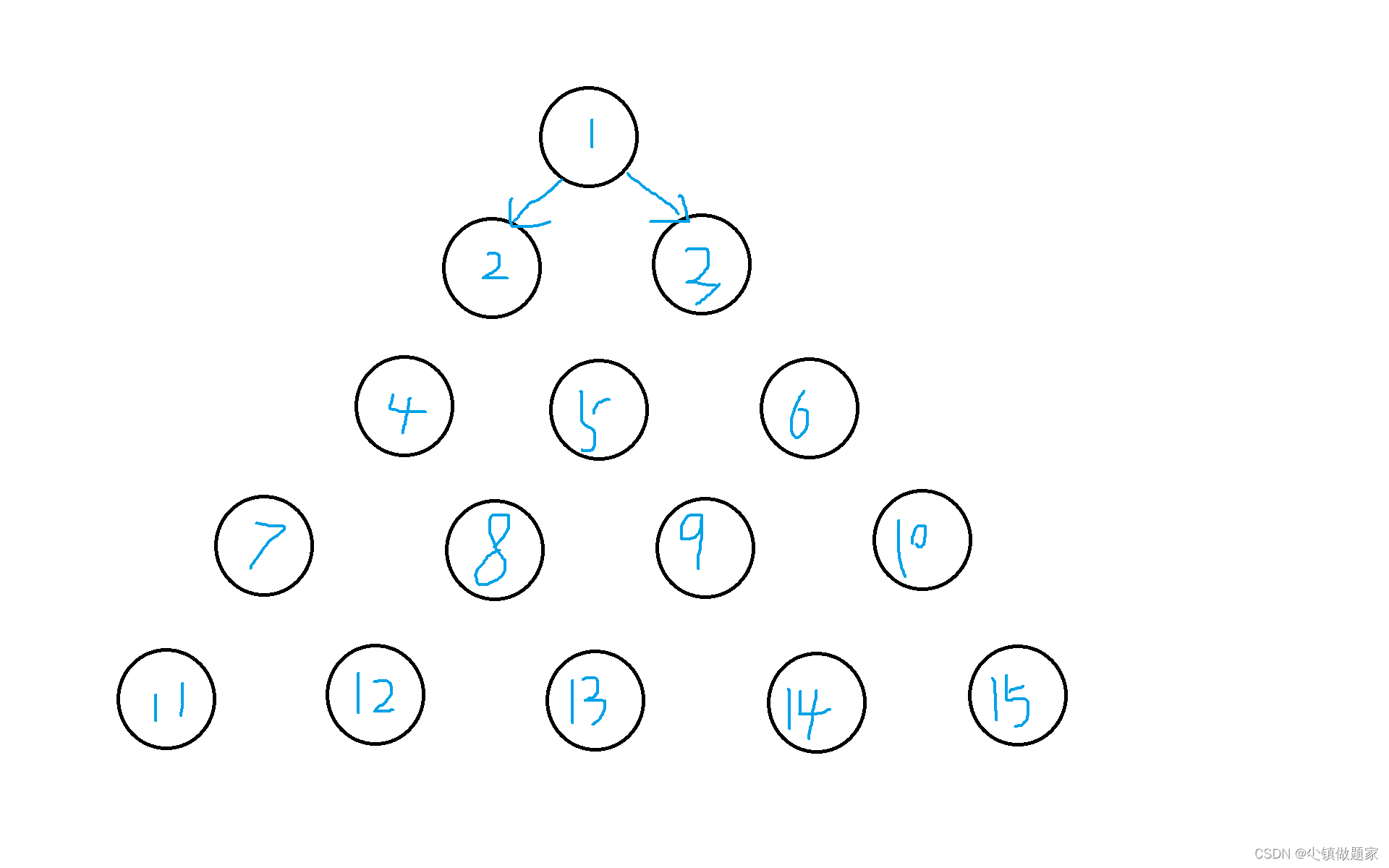
也就是可以走序号为2或者序号为3的节点，再看第三行：

 

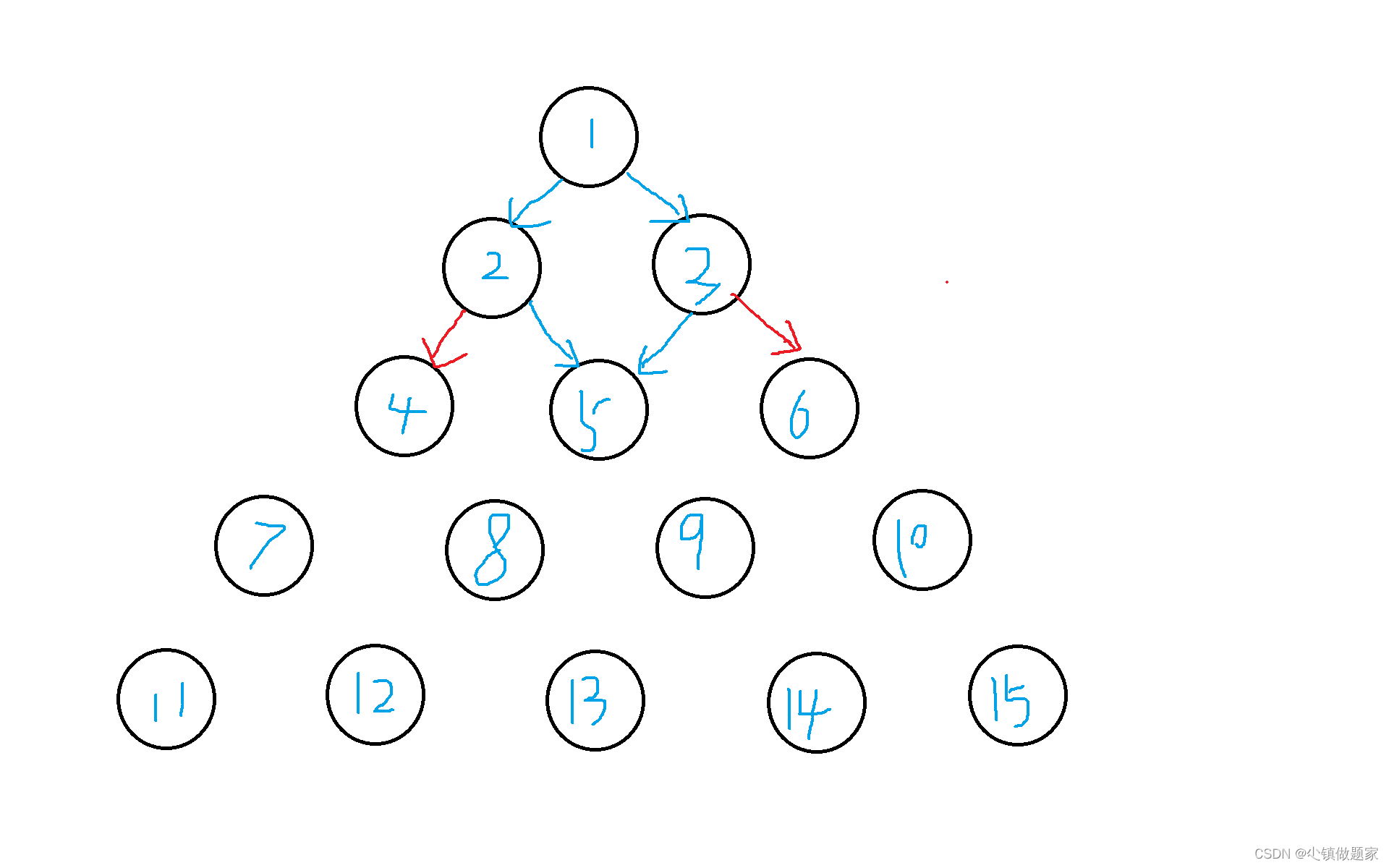
能走的只有序号为5的节点，为什么呢？因为如果连续两行都走最左边或者最右边，就不满足题目要求了（标红部分）。依次类推，我们再看第四行:

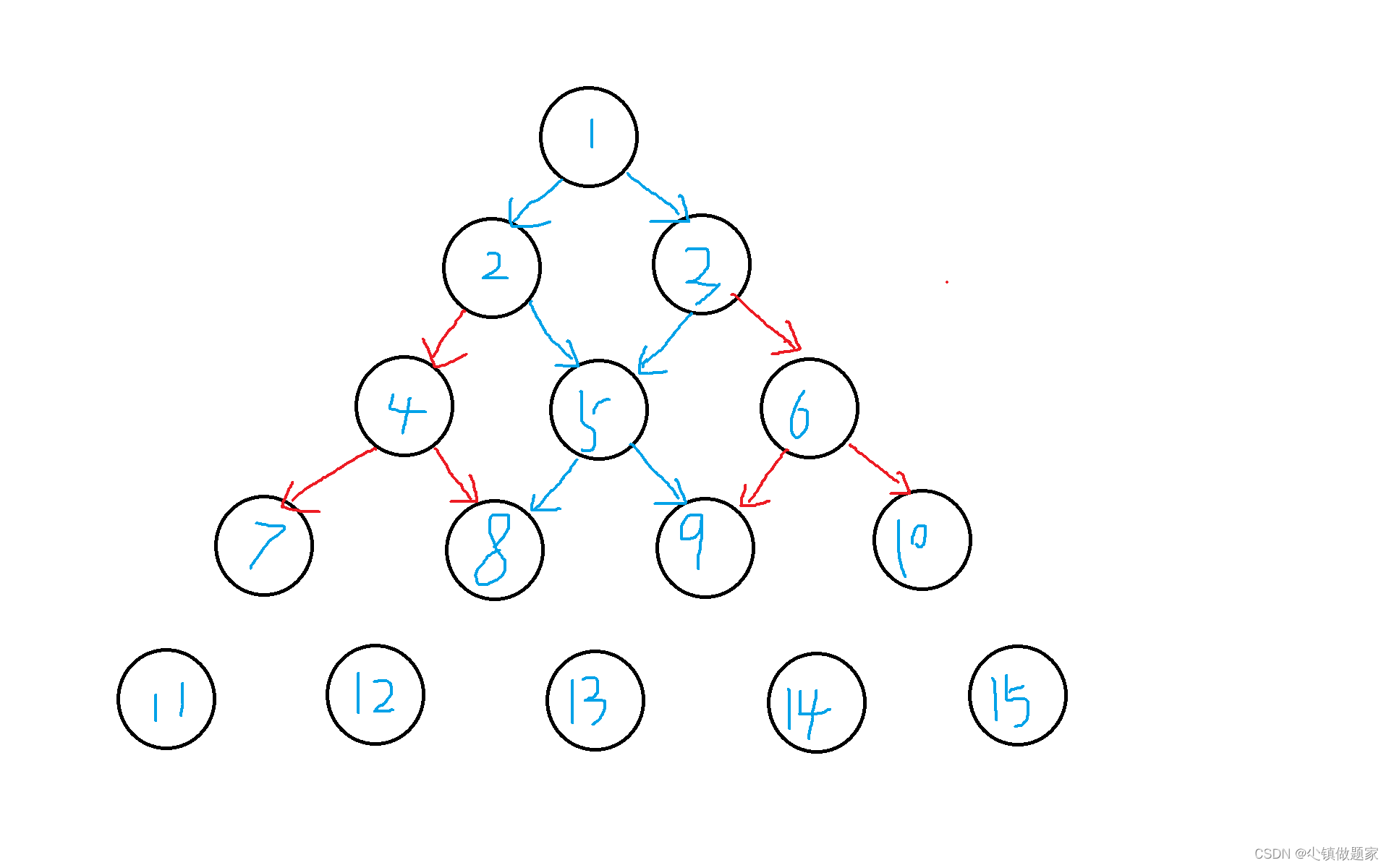
        第四行也是同理，因为第三行能走的，只有序号为5的节点，也就是说，第四行也只能从8或者9选一个来走，至于7和10是肯定不行的（因为上一行的节点也不满足题目条件）。

        接着到第五行，就能看出规律了：

        

        好像回到了奇怪的起点是嘛？其实这样画个图，这道题的特点就出来了。

        能走，或者说能选的节点，是有限的，当N为奇数的时候（第一行，第三行，第五行），只能选中间的节点；当N为偶数的时候（第二行，第四行）可以选中间的两个节点，根据题目要求，我们就需要选出这两个节点中的最大的一个节点即可。

        这道题的核心规律我们找到了，就是根据N来选择节点。那么节点该如何进行计算呢？题目不止要求 向左下走的次数与向右下走的次数相差不能超过 1。  还要求找到最大的和。

        根据题目要求来想，我们的答案肯定是在最后一层的，也就是说，我们需要将上一层对应位置也选出最大的两个值，上一个也是，根据dp的定义，所以要从第二行开始计算添加上第一行的对应位置的最大值，也就是说，我们是从上往下进行状态转移。

        接下来找一下状态转移方程。

        照例，先把题目的数据再粘贴一份，方便后面对比和进行查找：

5 //三角形的行数
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

        假设第二行的第一个数字，因为第一行只有一个数字，那么第二行的两个值都是只能加上第一行的数值，所以看不出什么。

        PS：这里的第二行，分别是3+7和8+7哦，之后同理。

        

        再看第三行，因为题目要求，从上往下走，只能走左下或者右下。

        

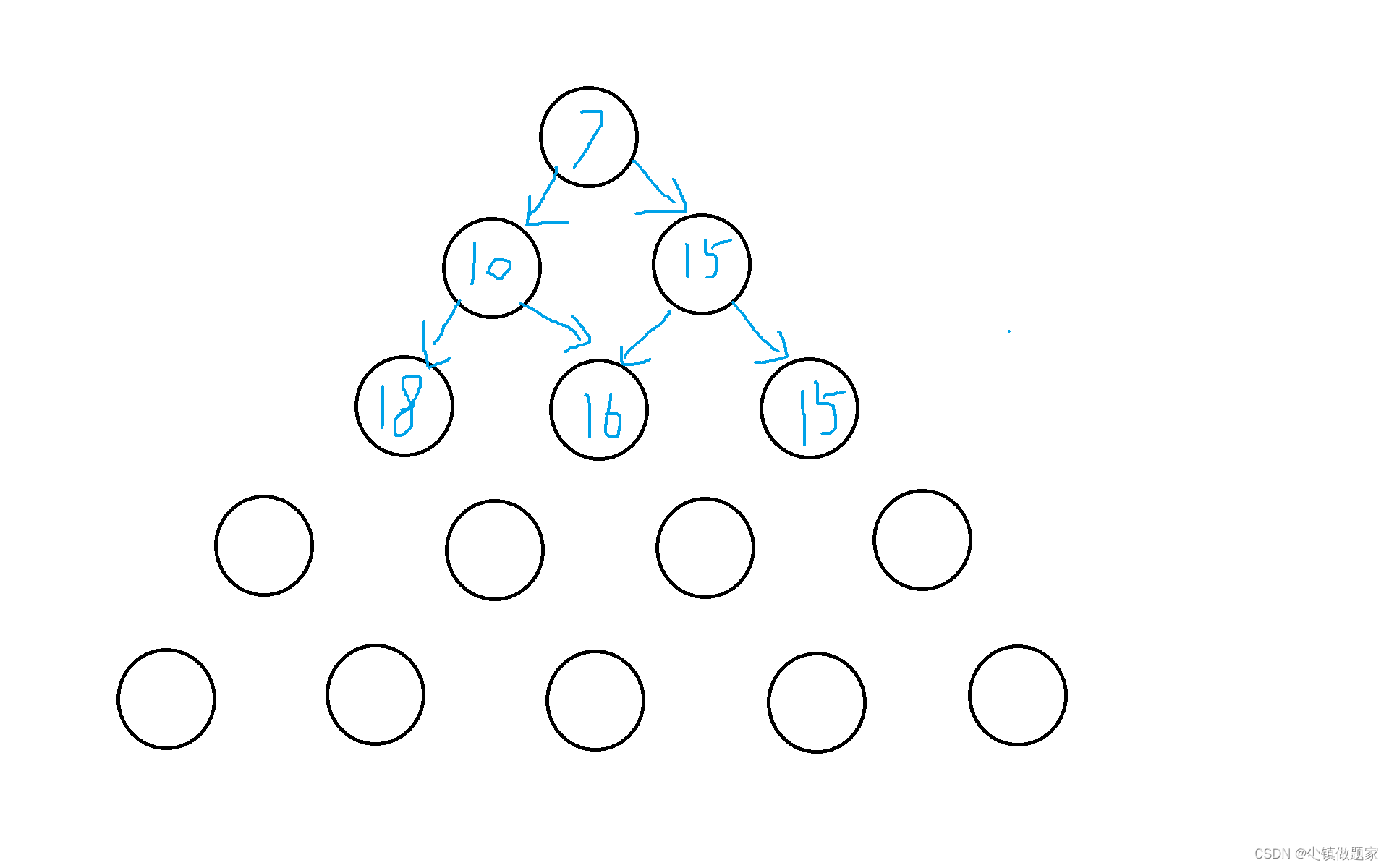
        因为第三行的8，只有10经过它，所以只能选10，也就是8+10。然后第三行的1，因为10和15 都经过它，所以它可以选二者之中的最大值，也就是15，所以是1+15。第三行的0，同理，只有15经过它，它也只能+15。

        其实到这里，状态转移方程就可以看出来了，怕大家还是有点懵，我直接把5行都说完，在讲规律，或者说状态转移方程。

        继续看第四行：

        

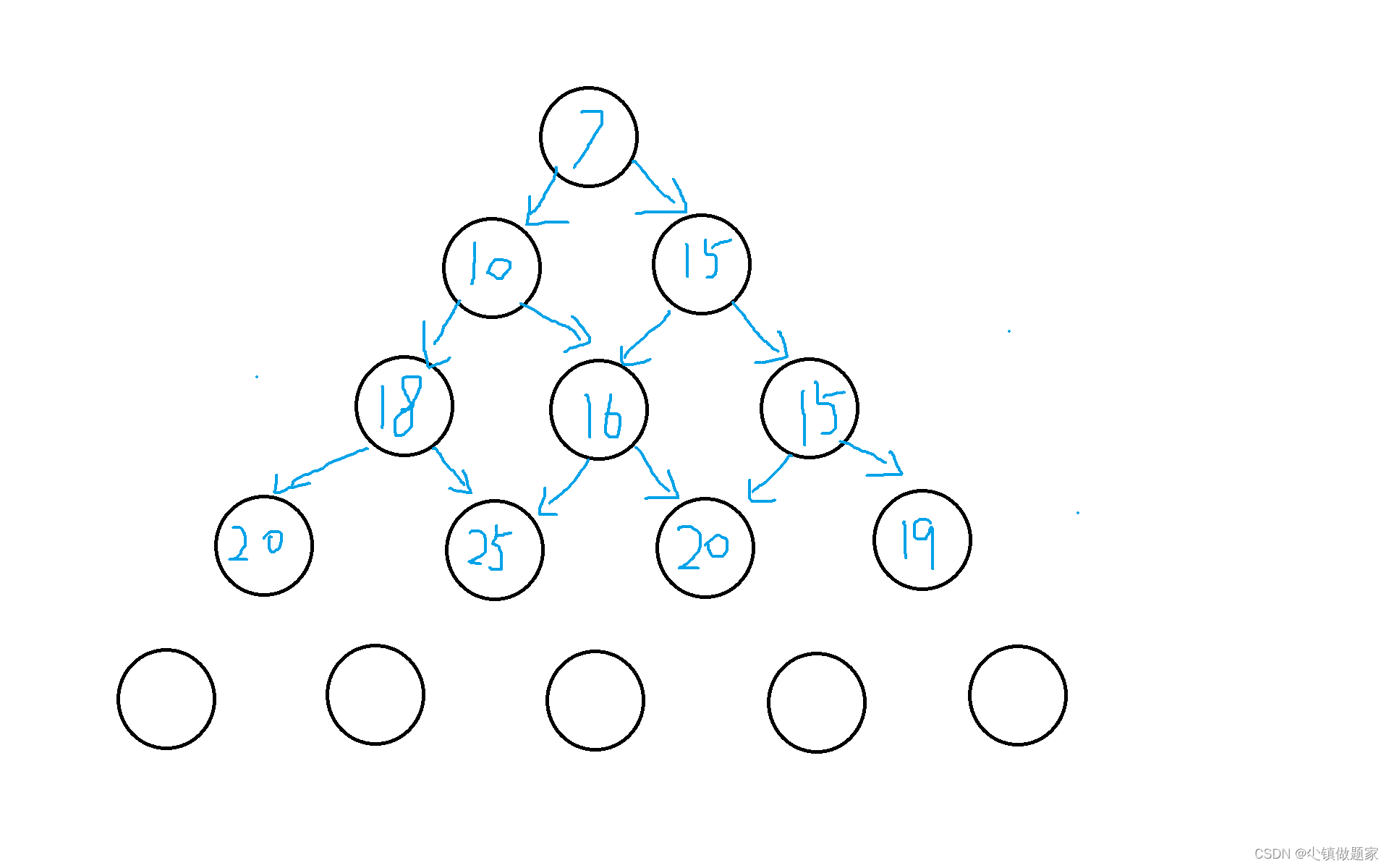
         第四行的四个节点分别是2，7，4，4。怕大家忘记，我先写出来，再继续找。

                第一个节点是2，只有18经过它，所以它的值只能为2+18 = 20

                第二个节点是7，有18和16经过它，所以选最大值18，得到7+18 = 25

                第三个节点是4，有16和15经过它，所以选最大值16，得到4+16 = 20

                第四个节点是4，只有15经过它，所以它的值只能为4+15 = 19。

        继续看第五行：

        

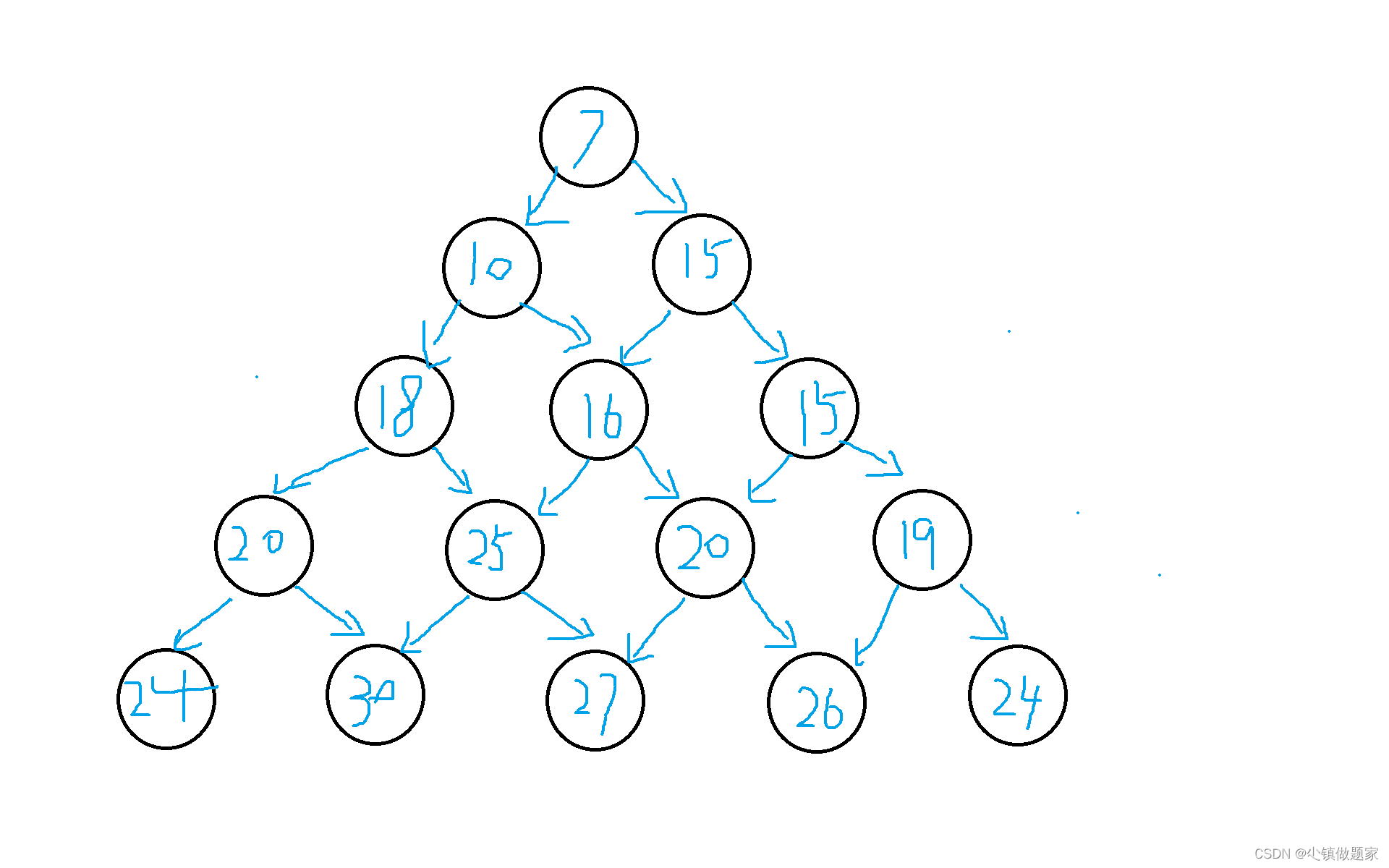
         第五行有5个节点，分别是4，5，2，6，5

                第一个节点，因为只有20经过它，所以它的值只能是4+20 = 24

                第二个节点，有20和25经过它，所以选最大值25，5+25 = 30

                第三个节点，有25和20经过它，所以选最大值25，2+25 = 27

                第四个节点，有20和19经过它，所以选最大值20，6+20 = 26

                第五个节点，只有19经过它，所以它的值只能是5+19 = 24。

        其实到这里，大家都应该发现规律了吧？

        从第二行开始，它的状态转移方程有两种情况：

1. 当前节点是该行的第一个节点，它的值只能加上上一行的第一个节点
2. 它的值就是加上上一行的前一个节点，上一行的当前节点，两个节点中的最大值     
3. 最后一个节点不也是只添加上一个的最后一个节点嘛？因为我们开数组的时候，会防止下标越界，同时也方便处理，会多开一列，所以我们可以看作，每一行还多出一个为0的节点，这样最后一个节点也可以使用第二种情况了。          

        所以状态转移方程就是

        为第一个节点时 dp[i][j] += dp[i-1][j];

        其他情况时 dp[i][j] += Math.max( dp[i-1][j-1] , dp[i-1][j] );

        然后根据N的奇偶情况，选择最后一行的对应节点输出即可。

        选择对应节点：N为奇数时，选择中间的节点。N为偶数时，选择中间两个节点的最大值节点

AC代码（Java）：

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt();
        int[][] dp = new int[N][N+1];
        for(int i = 0;i<N;i++){
          //第二行的数字数量是i+1
          for(int j = 0;j<i+1;j++){
            dp[i][j] = scan.nextInt();
          }
        }
        //因为题目是要求，向左下走的次数与向右下走的次数相差不能超过 1。也就是要从最后一层开始查找结果，dp就自上向下
        for(int i = 1;i<N;i++){
          for(int j = 0;j<i+1;j++){
            //如果是每一行的第一个，只能加上上一行的第一个，否则就是上一行的前一个和上一个的对应位置
            dp[i][j] += j==0 ? dp[i-1][j] : Math.max(dp[i-1][j-1],dp[i-1][j]);
          }
        }
        //如果N是奇数，那么最后一行只有一个值可以满足
        //如果N是偶数，那么需要在两个节点中间找到最大的那个节点
        int ans = N%2 == 0 ? Math.max(dp[N-1][N/2],dp[N-1][N/2-1]) : dp[N-1][N/2];
        System.out.println(ans);
        scan.close();
    }
}