EasyNVR平台优秀的视频能力在于通过RTSP/ONVIF协议,将前端接入设备的音视频资源进行采集,并转码成适合全平台、全终端分发的视频流格式,包括RTSP、RTMP、FLV、HLS、WebRTC等格式。平台可拓展性强、部署轻快,在安防监控领域有着广泛的使用场景,包括智慧工地、智慧工厂、智慧景区、智慧水利等等。
有用户反馈,EasyNVR服务会频繁自动重启,请求我们协助排查。
排查步骤如下:
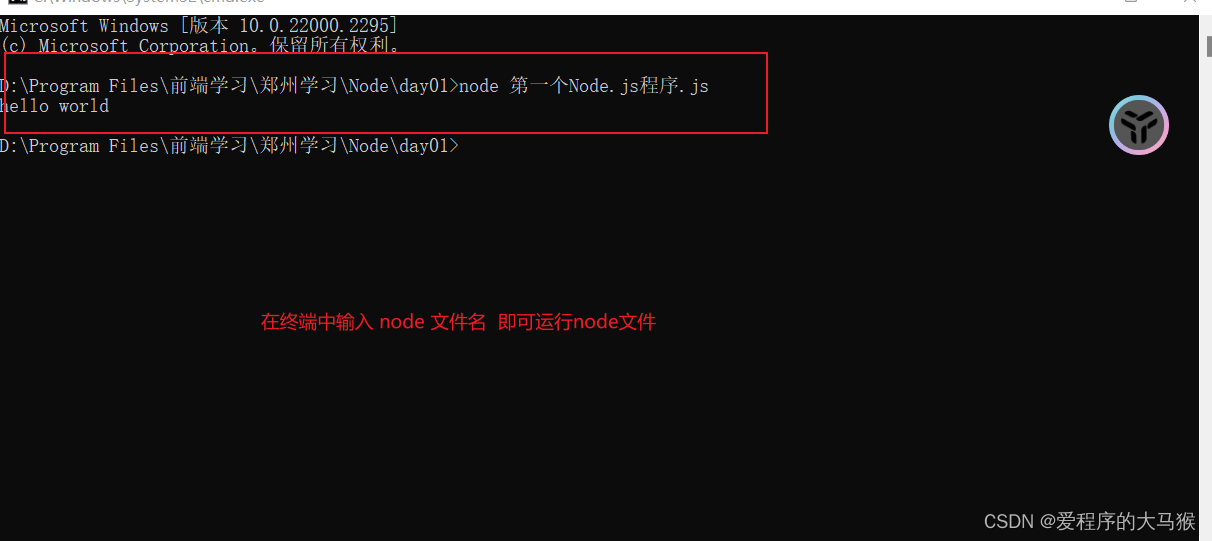
1)根据用户的反馈截图,我们看到EasyNVR服务一直在重启导致报错;

添加图片注释,不超过 140 字(可选)
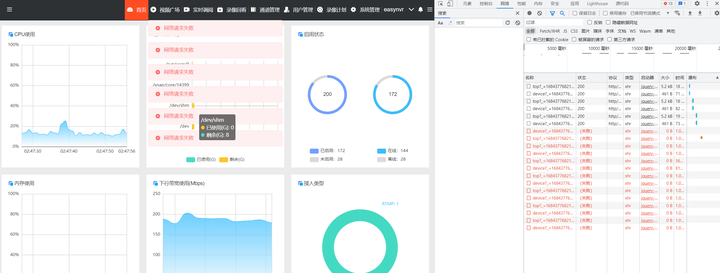
添加图片注释,不超过 140 字(可选)
2)登入EasyNVR服务器查看端口,发现并没有被占用;

添加图片注释,不超过 140 字(可选)
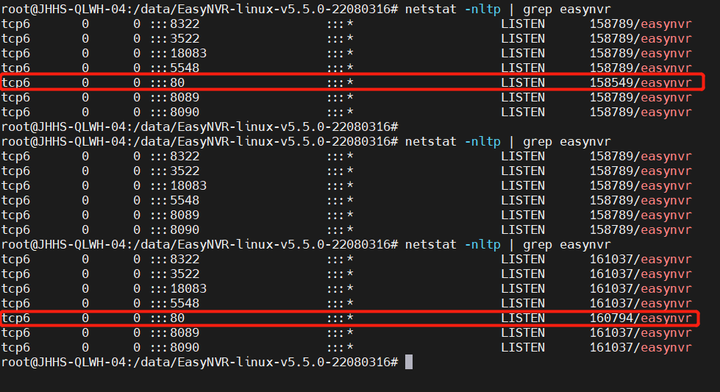
添加图片注释,不超过 140 字(可选)
3)查看log日志,也没有任何异常现象;

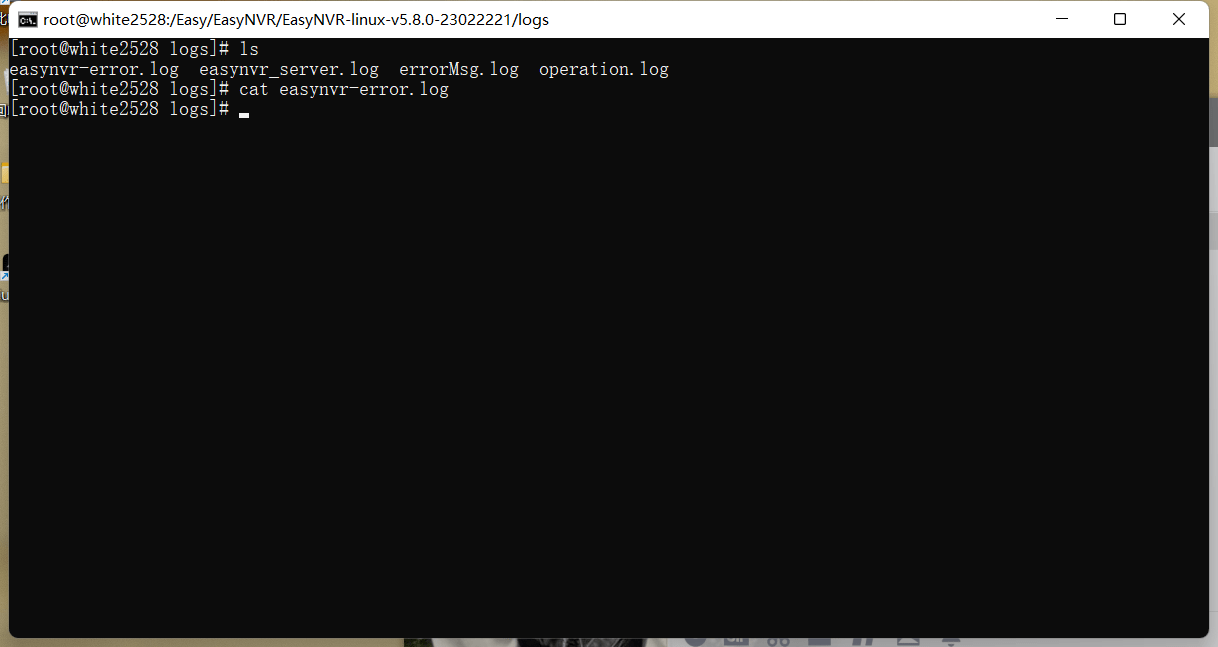
4)和用户沟通后发现,用户设备中有三个RTMP接入,关闭后服务恢复正常;
5)经过排查,原来是RTMP流输入错误,导致服务一直自启动,更改后服务恢复正常运行。


EasyNVR平台的可拓展性强、部署轻快、操作便捷,API简单易用。平台具备视频直播监控、录像、检索与回看、云存储、国标级联等功能,在安防监控领域有着广泛的使用场景。
编辑切换为居中
添加图片注释,不超过 140 字(可选)