目录
- 一、服务器信息
- 二、服务器基本信息及相关概念
- 2.1、服务器基本信息
- 2.2、LEO的概念
- 2.3、HW的概念
- 三、Follower故障处理细节
一、服务器信息
- 三台服务器
原始服务器名称 原始服务器ip 节点 centos7虚拟机1 192.168.136.27 broker0 centos7虚拟机2 192.168.136.28 broker1 centos7虚拟机3 192.168.136.29 broker2
二、服务器基本信息及相关概念
2.1、服务器基本信息
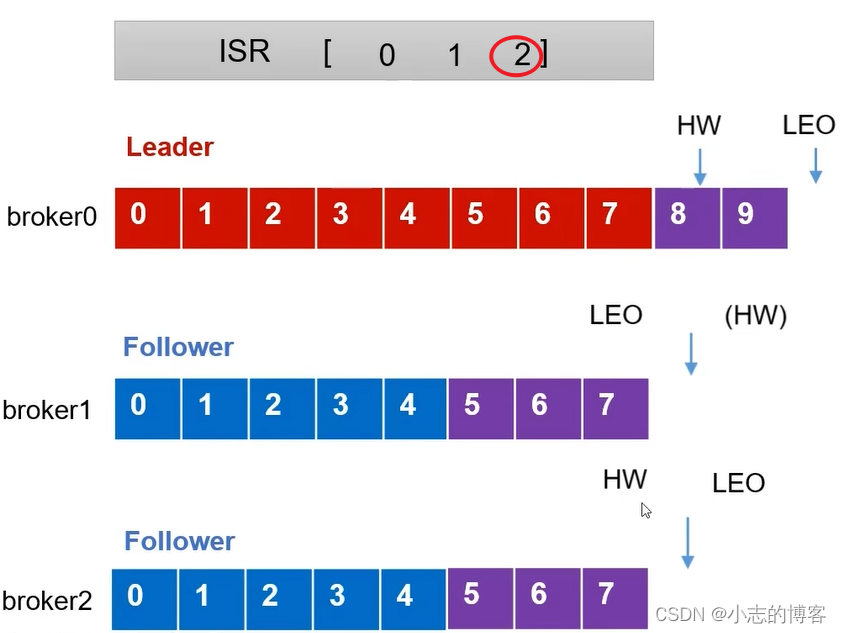
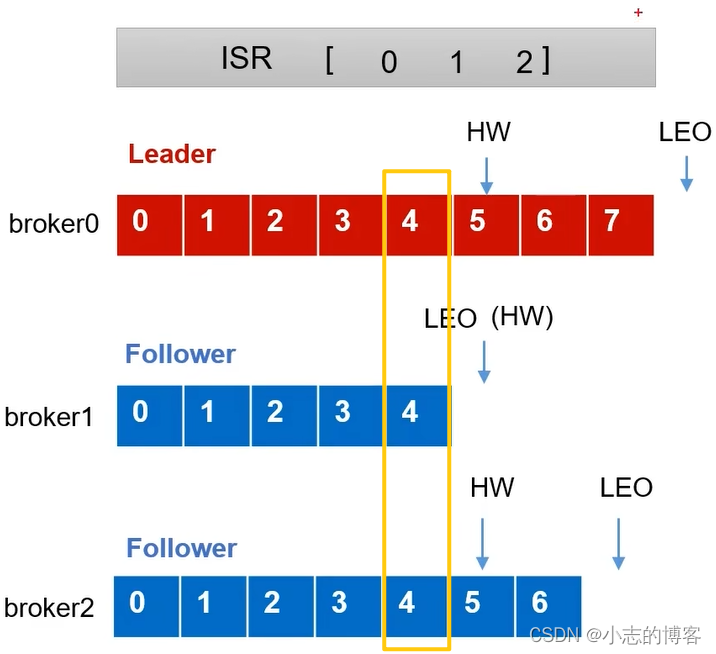
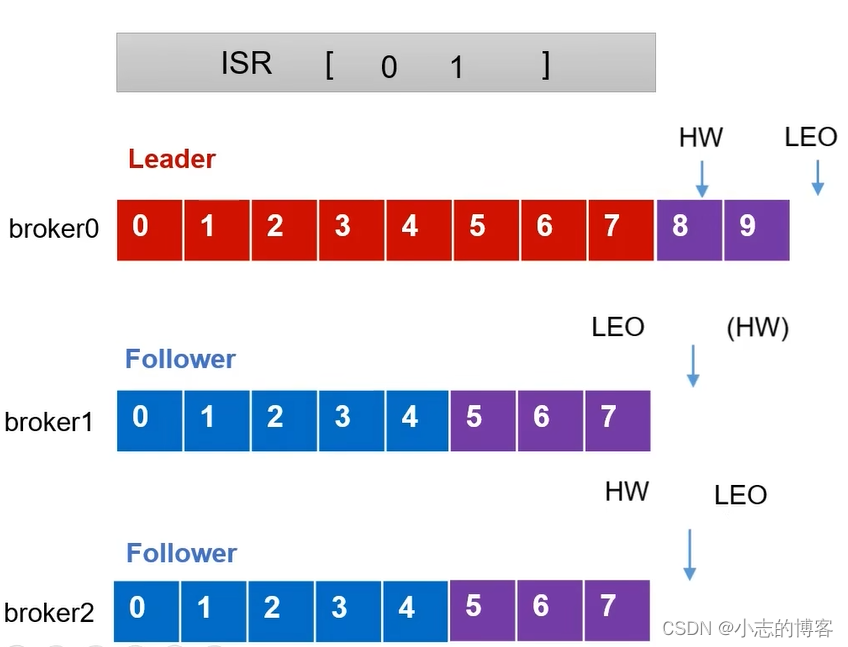
- 首先,分别有3台服务器分别为broker0、broker1、broker2,其中一台为leader,2台follower服务器。每台服务器已经接收到数据,如下图所示:
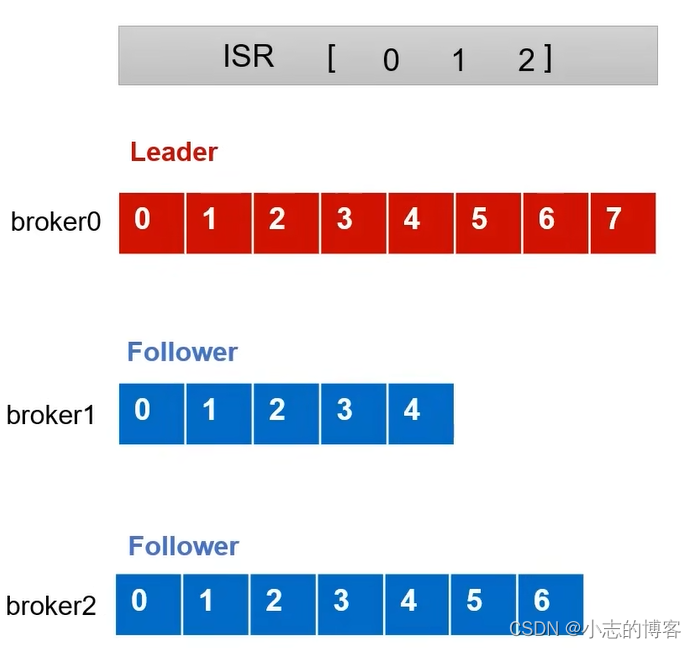
2.2、LEO的概念
- LEO(Log End Offset):每个副本的最后一个offset,LEO其实就是最新的offset + 1
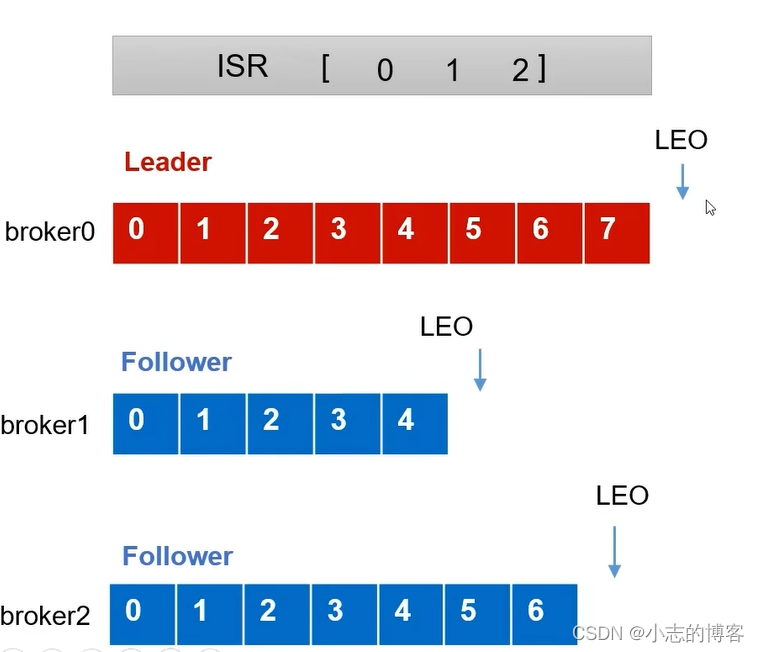
2.3、HW的概念
-
HW(High Watermark ):高水位线,所有副本中最小的LEO+1。如下图中每个broker都有的数据是4(即最小的LEO为4),HW为最小的LEO+1,
三、Follower故障处理细节
-
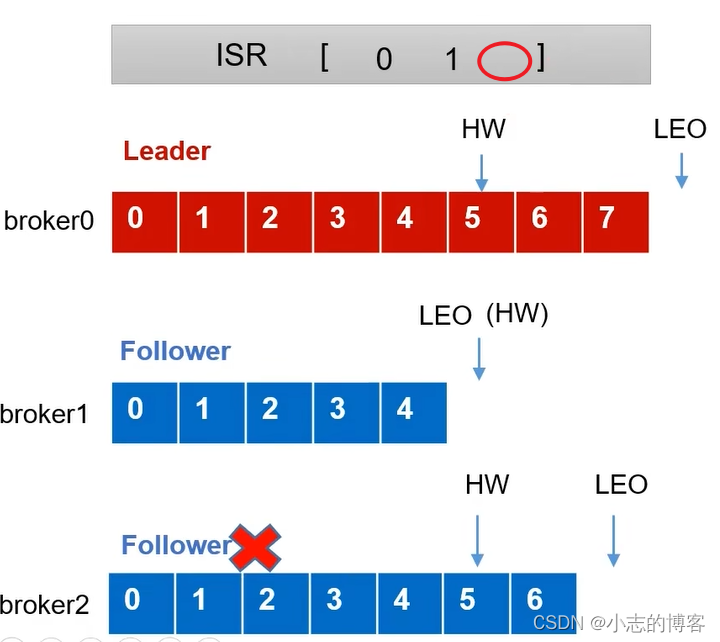
Follower发生故障后会被临时踢出ISR,如下图所示:
-
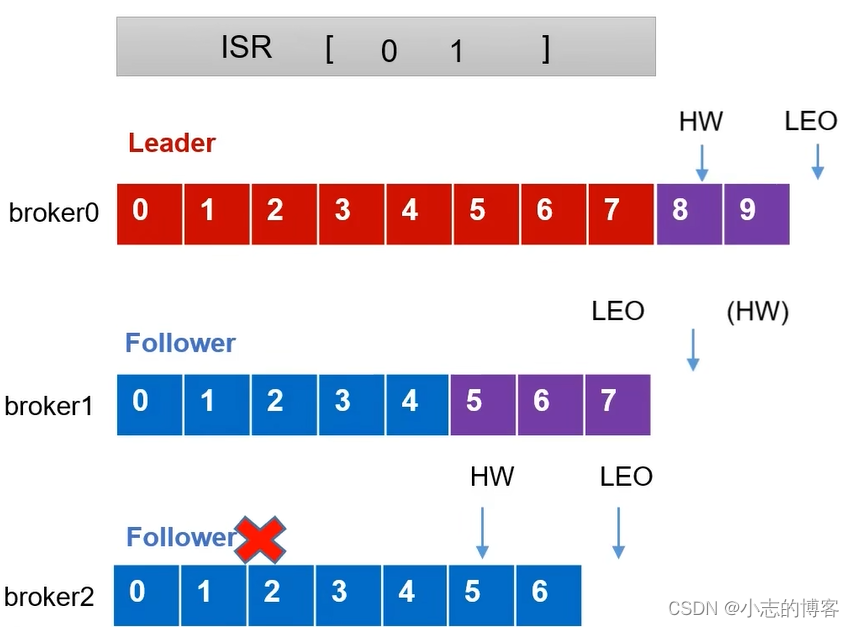
这个期间broker0中的Leader和broker1Follower继续接收数据,HW和LEO位置会随着接收数据的变化而变化,如下图所示:
-
待该Follower恢复后,Follower会读取本地磁盘记录的上次的HW,并将log文件高于HW的部分截取掉,从HW开始向Leader进行同步。
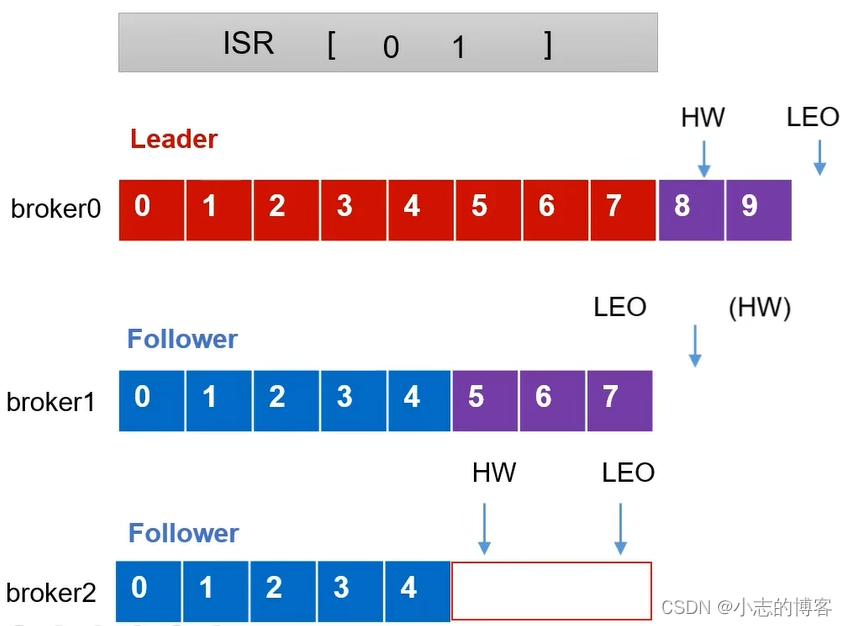
- 等该Follower 的LEO 大于等于该Partition 的HW,即Follower追上Leader之后,就可以重新加入ISR了,如下图所示: