基于龙格-库塔算法优化的BP神经网络(预测应用) - 附代码
文章目录
- 基于龙格-库塔算法优化的BP神经网络(预测应用) - 附代码
- 1.数据介绍
- 2.龙格-库塔优化BP神经网络
- 2.1 BP神经网络参数设置
- 2.2 龙格-库塔算法应用
- 4.测试结果:
- 5.Matlab代码
摘要:本文主要介绍如何用龙格-库塔算法优化BP神经网络并应用于预测。
1.数据介绍
本案例数据一共2000组,其中1900组用于训练,100组用于测试。数据的输入为2维数据,预测的输出为1维数据
2.龙格-库塔优化BP神经网络
2.1 BP神经网络参数设置
神经网络参数如下:
%% 构造网络结构
%创建神经网络
inputnum = 2; %inputnum 输入层节点数 2维特征
hiddennum = 10; %hiddennum 隐含层节点数
outputnum = 1; %outputnum 隐含层节点数
2.2 龙格-库塔算法应用
龙格-库塔算法原理请参考:https://blog.csdn.net/u011835903/article/details/122254286
龙格-库塔算法的参数设置为:
popsize = 20;%种群数量
Max_iteration = 20;%最大迭代次数
lb = -5;%权值阈值下边界
ub = 5;%权值阈值上边界
% inputnum * hiddennum + hiddennum*outputnum 为阈值的个数
% hiddennum + outputnum 为权值的个数
dim = inputnum * hiddennum + hiddennum*outputnum + hiddennum + outputnum ;% inputnum * hiddennum + hiddennum*outputnum维度
这里需要注意的是,神经网络的阈值数量计算方式如下:
本网络有2层:
第一层的阈值数量为:2*10 = 20; 即inputnum * hiddennum;
第一层的权值数量为:10;即hiddennum;
第二层的阈值数量为:10*1 = 10;即hiddenum * outputnum;
第二层权值数量为:1;即outputnum;
于是可知我们优化的维度为:inputnum * hiddennum + hiddennum*outputnum + hiddennum + outputnum = 41;
适应度函数值设定:
本文设置适应度函数如下:
f
i
t
n
e
s
s
=
a
r
g
m
i
n
(
m
s
e
(
T
r
a
i
n
D
a
t
a
E
r
r
o
r
)
+
m
e
s
(
T
e
s
t
D
a
t
a
E
r
r
o
r
)
)
fitness = argmin(mse(TrainDataError) + mes(TestDataError))
fitness=argmin(mse(TrainDataError)+mes(TestDataError))
其中TrainDataError,TestDataError分别为训练集和测试集的预测误差。mse为求取均方误差函数,适应度函数表明我们最终想得到的网络是在测试集和训练集上均可以得到较好结果的网络。
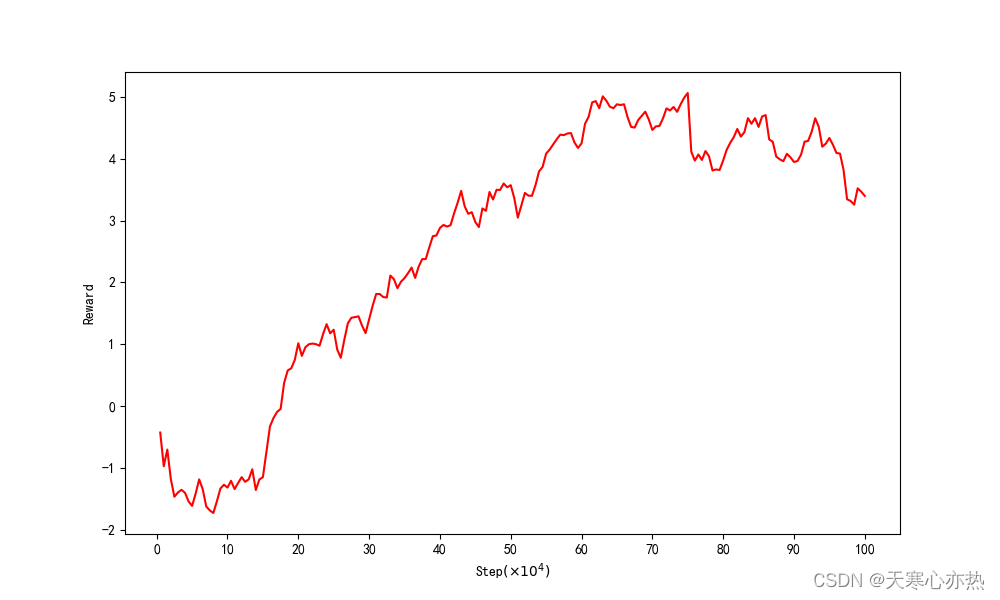
4.测试结果:
从龙格-库塔算法的收敛曲线可以看到,整体误差是不断下降的,说明龙格-库塔算法起到了优化的作用: