Particle Life粒子生命演化的MATLAB模拟

news2024/11/20 15:30:07

Particle Life粒子生命演化的MATLAB模拟

  • 0 前言
  • 1 基本原理
    • 1.1 力影响-吸引排斥行为
    • 1.2 距离rmax影响
  • 2 多种粒子相互作用
    • 2.1 双种粒子作用
    • 2.1 多种粒子作用
  • 3 代码

惯例声明：本人没有相关的工程应用经验，只是纯粹对相关算法感兴趣才写此博客。所以如果有错误，欢迎在评论区指正，不胜感激。本文主要关注于算法的实现，对于实际应用等问题本人没有任何经验，所以也不再涉及。

请添加图片描述

0 前言

Particle Life粒子生命演化最早是2017年由数字艺术家Jeffery Ventrella定义的，通过非常简单方法的定义粒子间的作用力，从而产生非常复杂的变化。

最开始Jeffery Ventrella管这种生成方法叫做Clusters，其思想来源于生物学家Lynn Margulus。每个粒子具有不同的颜色，每个颜色代表一种属性。粒子不仅会受到自己颜色粒子的吸引或排斥，也会受到其它颜色粒子的吸引和排斥。

在不同的参数下，粒子间会发生复杂的相互运动，某些参数会呈现出复杂的固定斑图，某些参数会呈现出类似生物之间的集群、逃跑、捕食等各种行为。

章节安排为：第一章主要是讲解原理，第二章演示一些基本的例子，第三章给出了基于MATLAB的具体代码。

本文的参考文献如下：
[1]粒子生命演化：由数量庞大的单体粒子演化出复杂的群体行为逻辑
https://www.bilibili.com/video/BV1Dh4y1t7hn/
https://www.youtube.com/watch?v=p4YirERTVF0
[2]https://particle-life.com
[3]blender3.6模拟-粒子生命-Particle Life
https://www.bilibili.com/video/BV1Ns4y1B7Fu/

1 基本原理

首先，假设一群粒子A，它们互相会受到其它粒子的作用力。两个粒子间的力大小是粒子间距离r的函数。

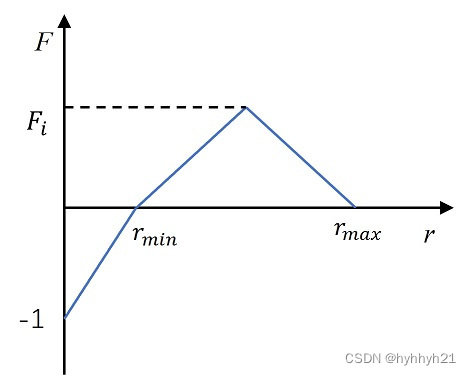
请添加图片描述

当距离r较小，小于rmin时，设置了-1的排斥力，为防止粒子之间重合。当粒子距离在rmin和rmax之间，粒子最大作用力为Fi。当粒子距离超过rmax，设置作用力为0，防止计算量过大。

当然有几个细节点需要注意：

1粒子所受的作用力只遵循上面的力方程，但不一定遵循牛顿第三定理。粒子的速度和加速度通过牛二律F=ma得到。由于防止粒子运动过快，还需要在全场设置粘滞阻尼。所以其实牛顿第一定理也不满足。当然由于这并不是精准的模拟仿真，所以这些小事可以忽略。

2力Fi是可以自行设置的，当Fi<0，粒子间呈现出排斥性，当Fi>0，粒子间呈现出吸引性，一般不超过±2；

3距离rmin通常在rmax的1/4~1/5左右；rmax和画布大小有关，rmax越大，越会有全局的粒子参与，rmax越小，粒子的行为越局部。

1.1 力影响-吸引排斥行为

当F<0时，粒子间呈现出排斥的现象：
请添加图片描述
当F>0时，粒子间呈现出吸引的现象：
请添加图片描述

1.2 距离rmax影响

这里画布大小都定义为1。
当rmax=0.2时，粒子的汇集效果如下：
请添加图片描述
当rmax=0.5时，粒子的汇集效果更全局化：
请添加图片描述

2 多种粒子相互作用

2.1 双种粒子作用

对于两种粒子A和B，力Fi共有4个，分别为A对A之间的力，A对B之间的力，B对A之间的力和B对B之间的力。这4个力可以写为一个矩阵形式：

AB
AF_AAF_AB
BF_BAF_BB

当假设A对A存在吸引，且A还会吸引B。但是B没有反向作用A的力，B与B之间也不会互相作用。这里的矩阵可以写作：
[ 1 0 0.5 0 ] \begin{bmatrix} 1 &0 \\ 0.5&0 \end{bmatrix} [10.5​00​]
此时得到的图形为细胞图案，A粒子在中间互相吸引到一团，周围吸引一圈B粒子。
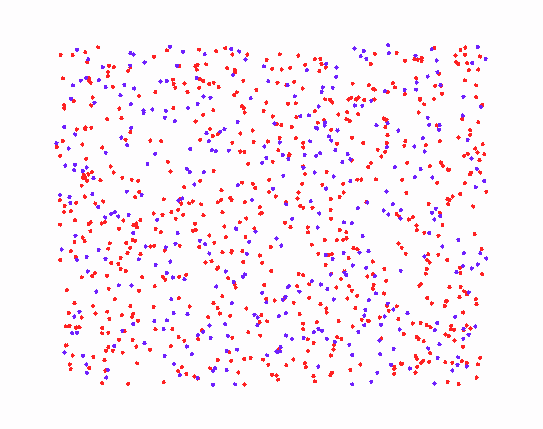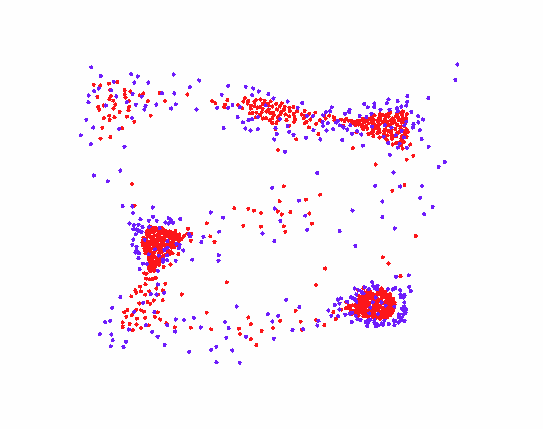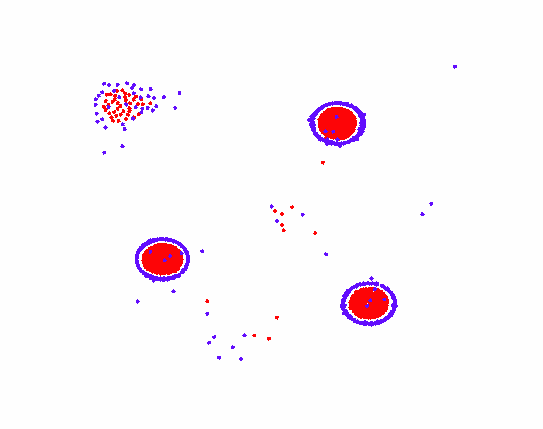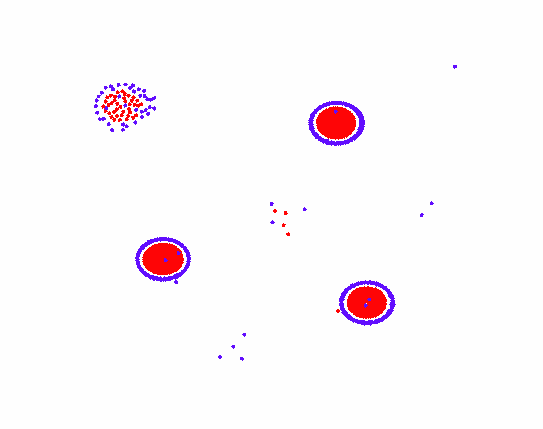
请添加图片描述
再添加两个规则给粒子B，粒子B之间会弱吸引，但粒子B排斥粒子A。此时由于粒子AB间一个吸引一个排斥，构成了不断向前运动的追逐系统。
[ 1 − 1 0.5 0.5 ] \begin{bmatrix} 1 &-1 \\ 0.5&0.5 \end{bmatrix} [10.5​−10.5​]
追逐模型如下：
请添加图片描述
之后多种粒子之间的运动规律，也是由上述各个规则叠加演化而成。
但是由于规则数量等于粒子种类N的平方，比如3种粒子就有9种粒子间规则，4种粒子就有16种粒子间规则。这就导致复杂性暴增，产生了无穷多的变化。

2.1 多种粒子作用

由于规则的复杂性，每一次随机出的结果可能都是独一无二的，且是其它人都未曾见过的。这种随机性和复杂性正是Particle Life的迷人之处。

下面列举一些演示计算结果
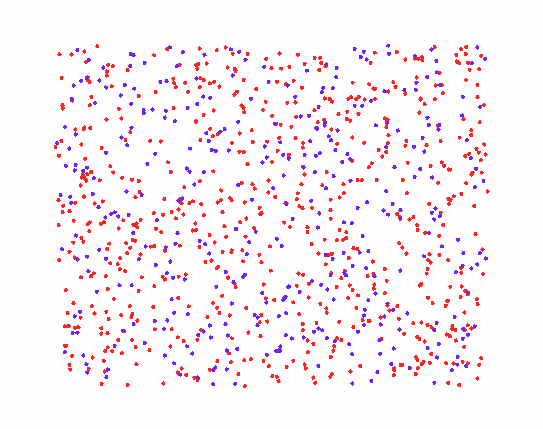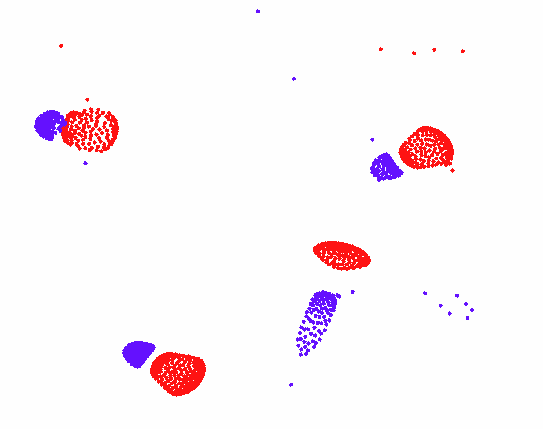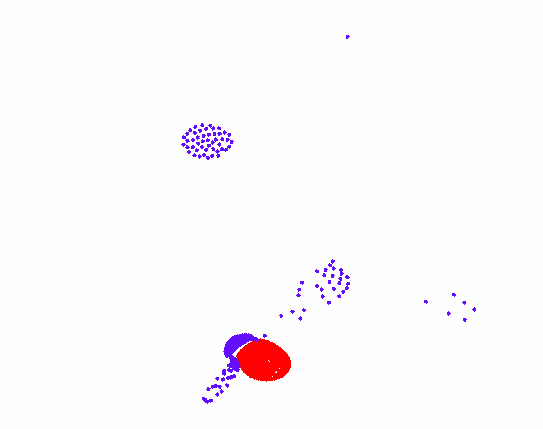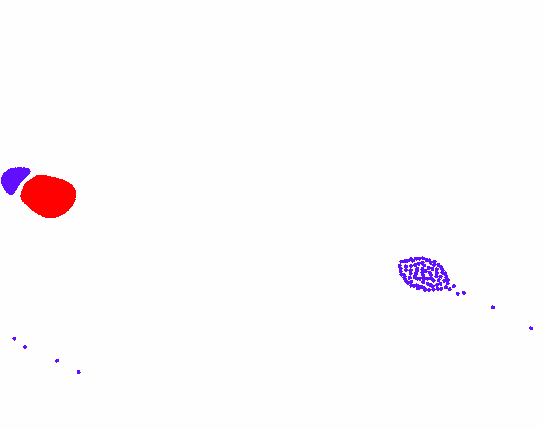
三种粒子，细胞图案：
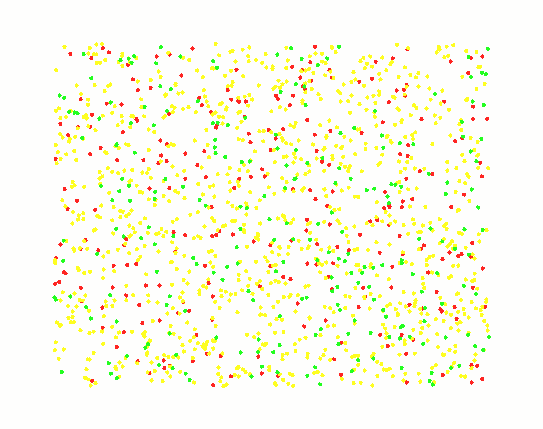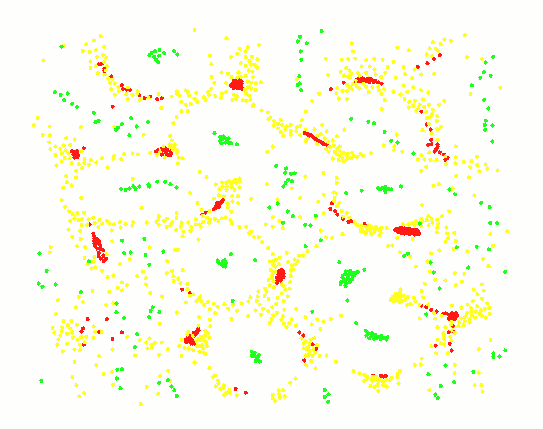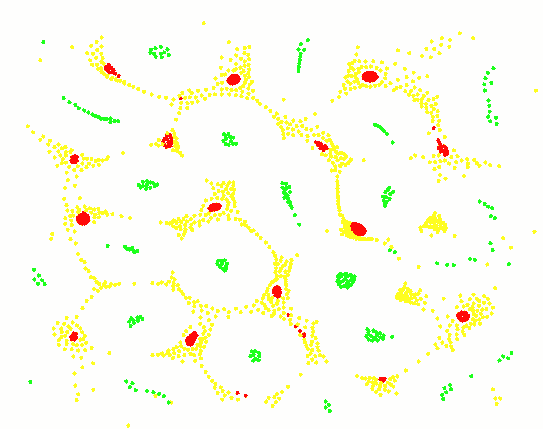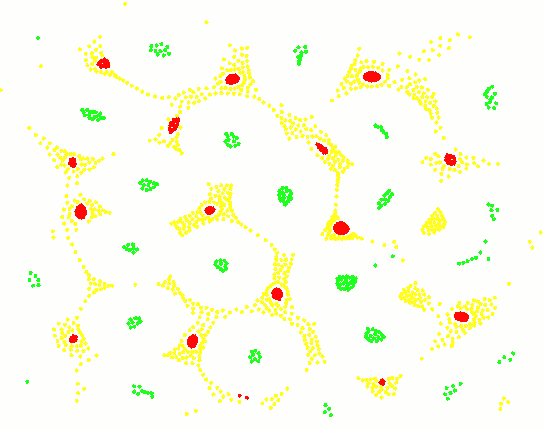
请添加图片描述
三种粒子，岛屿图案：
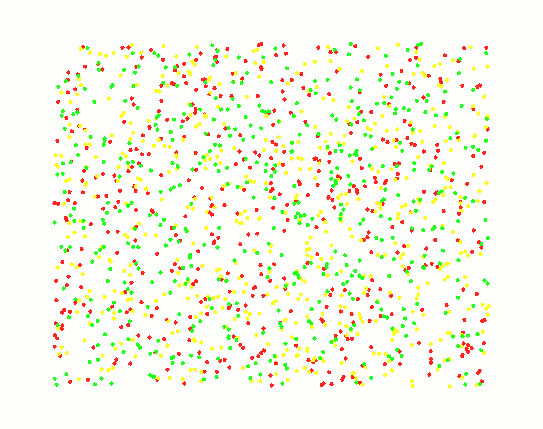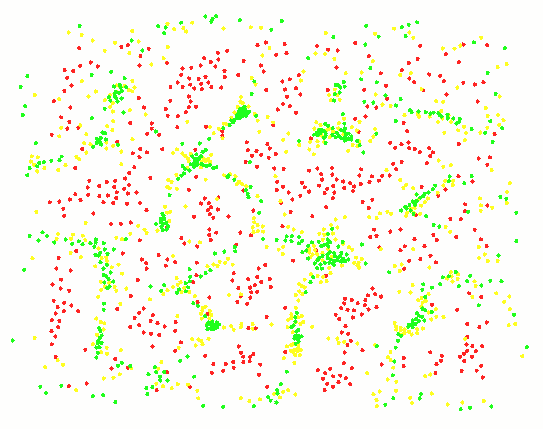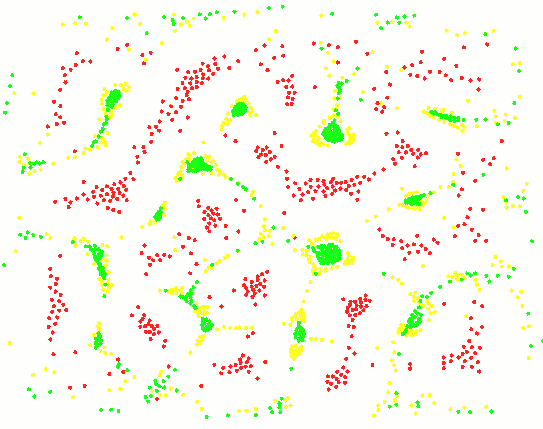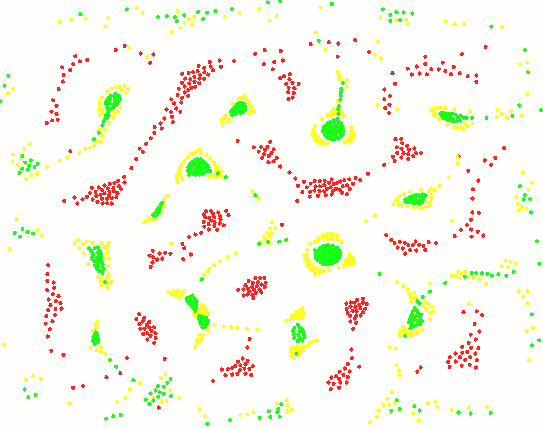
请添加图片描述

三种粒子，循环捕食图案：
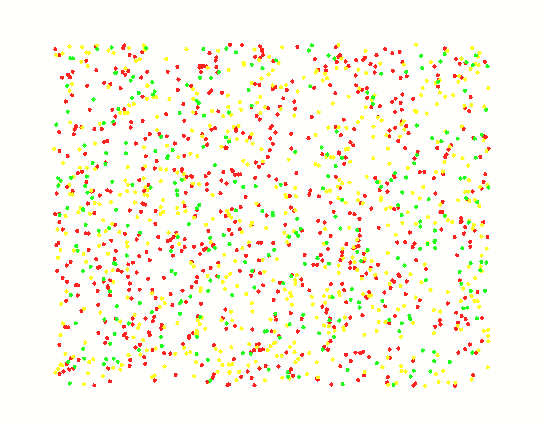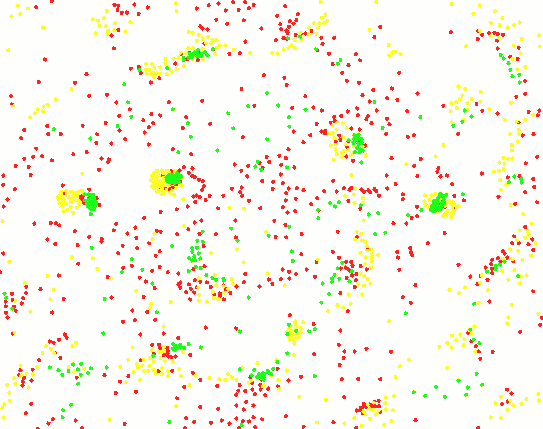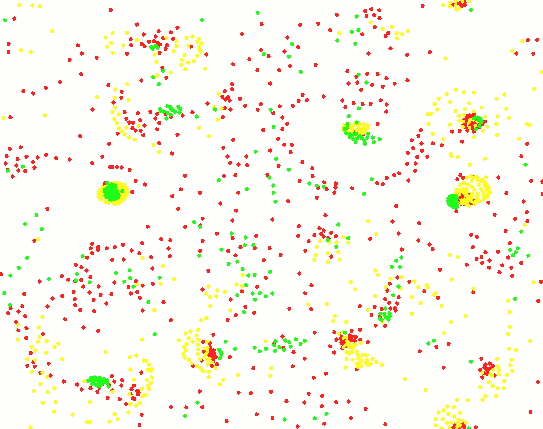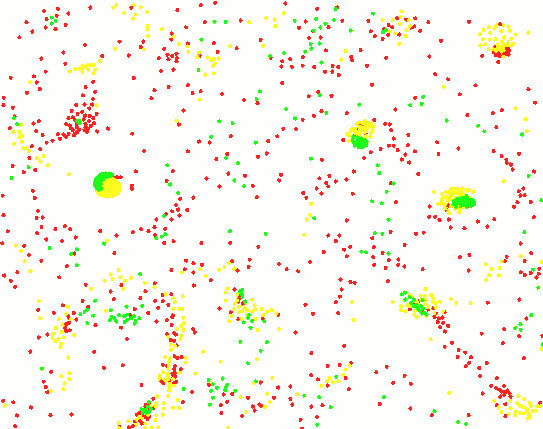
请添加图片描述
5种粒子的交互作用，呈现出一定的结构：
请添加图片描述

3 代码

上面绘图代码见文末。

主要更改粒子数量N，颜色数量NColor即可。建议粒子数量N大概是500倍颜色数量。不易太多，由于MATLAB运行效率较低，所以按照实际电脑配置自行更改。

力的作用距离Rmax在最好是1/c的形式，c是一个整数。

迭代总步数StepMax越大，展示的时间越长。这个如果想长时间欣赏粒子间作用，可以选择一个比较大的数。

图像刷新频率FrameFreq是用来控制多少个时间步显示一次。一般选择2就行，太大会有卡顿的感觉。

clear
clc
close all
%Particle Life粒子生命 MATLAB代码

%% 初始设定参数
%初始设定
rng('shuffle');%随机种子
N=1500;%粒子数量
NColor=3;%颜色数量
Ni=rand(NColor,1);Ni=round(Ni*N/sum(Ni));%随机分配每个颜色对应的粒子数量
N=sum(Ni);

Rmax=1/5;%力作用的距离
mcp=hsv(40);colormap(mcp(1:32,:));%定义展示颜色
StepMax=1.2e3;%结束迭代时间步
FrameFreq=2;%刷新率，正整数，最小为1，越大图像刷新越慢
%% 其它默认参数
%绘图范围
Xlim=[0,1];
Ylim=[0,1];
%定义每个粒子颜色编号
ColorP=zeros(N,1);
for t=1:NColor
    ColorP(1+sum(Ni(1:t-1)):sum(Ni(1:t)))=t;
end
%粒子的力关系矩阵
FMat=rand(NColor,NColor)*3-1.5;%所有力Fi在-1.5~1.5之间
%粒子坐标速度
XY_P=rand(N,2)*0.8+0.1;%所有粒子点坐标
VXY_P=zeros(N,2);%粒子点速度


Rmin=Rmax/5;%粒子间的最小作用距离
MeshMax=1/Rmax;%网格数量
dt=5e-3;%时间精度

%构建力函数
t=0;%初始时间
c=Rmax*15.0*sqrt(N);%阻尼，为了防止粒子运动速度太快

%% 循环计算每一步迭代
tJ=0;%绘图计数
for kt=1:StepMax
    %计算点对应的网格
    XYindx=ceil(XY_P/Rmax);
    %循环计算每个点所受的力
    ForceP=zeros(N,2);
    for kp=1:N %循环每一个点
        %该点的颜色、坐标和网格
        Color_k=ColorP(kp,:);
        XY_k=XY_P(kp,:);
        XYindx_k=XYindx(kp,:);
        %计算周围点对该点的力
        F_k=FMat(Color_k,ColorP)';
        
        [Indx_t,XY_P_B,F_B]=Beside9(XYindx_k,XYindx,MeshMax,XY_P,F_k);%周边点索引

        ForceP_k=F_Func(XY_P_B-XY_k,F_B,Rmin,Rmax);
        ForceP(kp,:)=ForceP_k;
    end
    %增加阻尼项，和v相反
    ForceP=ForceP-c.*VXY_P;

    %根据F更新位移x和速度v。dv=at,dx=vt+at^2/2
    VXY_P_New=VXY_P+ForceP*dt;
    XY_P=XY_P+0.5*(VXY_P+VXY_P_New)*dt;
    VXY_P=VXY_P_New;

    %循环边界条件，如果超出边界，就移到另一端
    XY_P(XY_P>1)=XY_P(XY_P>1)-1;
    XY_P(XY_P<0)=XY_P(XY_P<0)+1;

    t=t+dt;%加一时间步
    if ~mod(kt,FrameFreq)
        f=figure(1);
        f.Color=[1,1,1];
        cla;
        scatter(XY_P(:,1),XY_P(:,2),6,ColorP,"filled");
        xlim([0,1]);ylim([0,1]);
        %set(gca,'XTick',[],'YTick',[])
        axis off
        pause(0.01)%每一帧图像停留时间
        tJ=tJ+1;
    end
end

%% 后置函数
function Ft2=F_Func(xy,F,rmin,rmax)
%粒子左右函数
%xy，N行2列的向量，代表别的点距离O点的距离向量
%F，N行1列的向量，代表吸引力F大小
rmid=0.5*(rmax+rmin);
dmid=0.5*(rmax-rmin);
r=sqrt(xy(:,1).^2+xy(:,2).^2);%距离
%r(r==0)=rmax;
Ft=zeros(size(r));
%第一段
indx1=(r<rmin);
Ft(indx1)=r(indx1)/rmin-1;
%第二段
indx_last=~indx1;
indx2=indx_last&(r<rmid);
Ft(indx2)=F(indx2).*(r(indx2)-rmin)/dmid;
%第三段
indx3=(r>=rmid)&(r<rmax);
Ft(indx3)=-F(indx3).*(r(indx3)-rmax)/dmid;
%计算力向量
dir_xy=xy./r;
dir_xy(isnan(dir_xy))=0;
Ft_Vec=dir_xy.*(Ft*ones(1,2));
%计算合力
Ft2=sum(Ft_Vec,1);
end

function [BesideIndx1,XY_P_B,F_P]=Beside9(XYindx0,XYindx1,NMesh,XY_P,F_P)
%寻找点0附近区域3×3共9格区域内
%开启循环边界条件

%复制出边界点，然后再计算。因为有的点在rmax较大的循环边界条件，会同时向上和下吸引
if XYindx0(1)==1
    %把最后一列复制一份到前面
    indx_t=XYindx1(:,1)==NMesh;
    XYindx1_t=XYindx1(indx_t,:);
    XYindx1_t(:,1)=0;%赋值为0
    XYindx1=[XYindx1;XYindx1_t];
    XY_P=[XY_P;XY_P(indx_t,:)+[-1,0]];
    F_P=[F_P;F_P(indx_t)];
end
if XYindx0(1)==NMesh
    %把第一列复制一份到最后
    indx_t=XYindx1(:,1)==1;
    XYindx1_t=XYindx1(indx_t,:);
    XYindx1_t(:,1)=NMesh+1;%赋值为NMesh+1
    XYindx1=[XYindx1;XYindx1_t];
    XY_P=[XY_P;XY_P(indx_t,:)+[1,0]];
    F_P=[F_P;F_P(indx_t)];
end
if XYindx0(2)==1
    %把最后一行复制一份到前面
    indx_t=XYindx1(:,2)==NMesh;
    XYindx1_t=XYindx1(indx_t,:);
    XYindx1_t(:,2)=0;%赋值为0
    XYindx1=[XYindx1;XYindx1_t];
    XY_P=[XY_P;XY_P(indx_t,:)+[0,-1]];
    F_P=[F_P;F_P(indx_t)];
end
if XYindx0(2)==NMesh
    %把第一行复制一份到最后
    indx_t=XYindx1(:,2)==1;
    XYindx1_t=XYindx1(indx_t,:);
    XYindx1_t(:,2)=NMesh+1;%赋值为NMesh+1
    XYindx1=[XYindx1;XYindx1_t];
    XY_P=[XY_P;XY_P(indx_t,:)+[0,1]];
    F_P=[F_P;F_P(indx_t)];
end
%夹在范围之内的点有哪些
BesideIndx_X=(XYindx0(1)-1<=XYindx1(:,1))&(XYindx1(:,1)<=XYindx0(1)+1);
BesideIndx_Y=(XYindx0(2)-1<=XYindx1(:,2))&(XYindx1(:,2)<=XYindx0(2)+1);
BesideIndx1=BesideIndx_X & BesideIndx_Y;
XY_P_B=XY_P(BesideIndx1,:);
F_P=F_P(BesideIndx1);
end

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/945610.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Android屏幕显示 android:screenOrientation configChanges 处理配置变更

Android屏幕显示 android:screenOrientation configChanges 处理配置变更

显示相关 屏幕朝向 https://developer.android.com/reference/android/content/res/Configuration.html#orientation 具体区别如下&#xff1a; activity.getResources().getConfiguration().orientation获取的是当前设备的实际屏幕方向值&#xff0c;可以动态地根据设备的旋…
阅读更多...
Windows10 系统安装教程

Windows10 系统安装教程

多虚不如少实。 一、 下载安装包 下载前景&#xff1a;网上下载的 windows10 系统一般都有捆绑软件&#xff0c;用户体验不爽&#xff0c;所以建议到 正规渠道下载 windows10 系统的不同版本。另外网上也有一些 windows10 系统的镜像文件 可以直接一键安装&#xff0c;…
阅读更多...
OpenShift 4 - 用 Prometheus 和 Grafana 监视用户应用定制的观测指标（视频）

OpenShift 4 - 用 Prometheus 和 Grafana 监视用户应用定制的观测指标（视频）

《OpenShift / RHEL / DevSecOps 汇总目录》 说明&#xff1a;本文已经在 OpenShift 4.13 的环境中验证 文章目录 OpenShift 的监控功能构成部署被监控应用用 OpenShift 内置功能监控应用用 Grafana 监控应用安装 Grafana 运行环境配置 Grafana 数据源定制监控 Dashboard 演示视…
阅读更多...
Python之动态规划

Python之动态规划

序言 最近在学习python语言&#xff0c;语言有通用性&#xff0c;此文记录复习动态规划并练习python语言。 动态规划&#xff08;Dynamic Programming&#xff09; 动态规划是运筹学的一个分支&#xff0c;是求解决策过程最优化的过程。20世纪50年代初&#xff0c;美国数学家…
阅读更多...
上滑动导航栏手势桌面最近任务可见解密-千里马手把手带你搞定framework车载车机系统开发

上滑动导航栏手势桌面最近任务可见解密-千里马手把手带你搞定framework车载车机系统开发

建议先看另一篇blog&#xff1a; https://blog.csdn.net/learnframework/article/details/123032419 系统如何让桌面执行对应的onStart方法呢&#xff1f; 具体的堆栈显示如下&#xff1a; makeActiveIfNeeded:5788, ActivityRecord (com.android.server.wm) makeVisibleIfNe…
阅读更多...
MOS管开关电路栅极为什么要串接电阻

MOS管开关电路栅极为什么要串接电阻

在MOS管开关电路或者驱动电路中&#xff0c;常常会在MOS管的栅极串接一个电阻。 这个电阻阻值一般是几十欧姆&#xff0c;那么这个电阻有什么作用呢&#xff1f; 第一个作用就是可以限制驱动电流 &#xff0c;防止瞬间驱动电流过大导致驱动芯片驱动能力不足或者损坏。 MOS管的…
阅读更多...
CANOCO5.0实现冗余分析（RDA）最详细步骤

CANOCO5.0实现冗余分析（RDA）最详细步骤

在地理及生态领域会常使用RDA分析&#xff0c;RDA的实现路径也有很多&#xff0c;今天介绍一下CANOCO软件的实现方法。 1.软件安装 时间调整到2010年 2.数据处理 得有不同的物种或者样点数值&#xff0c;再加上环境因子数据。 3.软件运行 4.结果解读 结果解读主要把握这几点…
阅读更多...
1、[春秋云镜]CVE-2022-32991

1、[春秋云镜]CVE-2022-32991

文章目录 一、相关信息二、解题思路&#xff08;手注&#xff09;三、通关思路&#xff08;sqlmap&#xff09; 一、相关信息 靶场提示&#xff1a;该CMS的welcome.php中存在SQL注入攻击。 NVD关于漏洞的描述&#xff1a; 注入点不仅在eid处&#xff01;&#xff01;&#xff…
阅读更多...
加油站【贪心算法】

加油站【贪心算法】

加油站 在一条环路上有 n 个加油站&#xff0c;其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车&#xff0c;从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发&#xff0c;开始时油箱为空。 给定两个整数数组 gas 和…
阅读更多...
Stable Diffusion Web UI的原理与使用

Stable Diffusion Web UI的原理与使用

Stable Diffusion是一套基于Diffusion扩散模型生成技术的图片生成方案&#xff0c;随着技术的不断发展以及工业界对这套工程细节的不断优化&#xff0c;使其终于能在个人电脑上运行&#xff0c;本文将从github下载开始讲一讲如何使用Stable Diffusion Web UI进行AI图像的生成。…
阅读更多...
el-table 单击某一行，该行的前面的多选框显示已勾选

el-table 单击某一行，该行的前面的多选框显示已勾选

目 录 官网&#xff1a; 1. 单页面 2. table是组件 案例&#xff1a; 官网&#xff1a; 1. 单页面 通过单击获取当前行的数据&#xff0c;然后传给选中显示勾选的方法。 <template><el-tableref"multipleTable":data"tableData"tooltip-eff…
阅读更多...
matlab使用教程(28)—微分方程(ODE)求解常见问题

matlab使用教程(28)—微分方程(ODE)求解常见问题

1.非负 ODE 解 本博客说明如何将 ODE 解约束为非负解。施加非负约束不一定总是可有可无&#xff0c;在某些情况下&#xff0c;由于方程的物理解释或解性质的原因&#xff0c;可能有必要施加非负约束。仅在必要时对解施加此约束&#xff0c;例如不这样做积分就会失败或者解将不…
阅读更多...
Unity Canvas动画不显示的问题

Unity Canvas动画不显示的问题

问题描述: 我通过角色创建了一个walk的动画&#xff0c;当我把这个动画给到Canvas里面的一个image上&#xff0c;这个动画就不能正常播放了&#xff0c;经过一系列的查看我才发现&#xff0c;canvas里面动画播放和非canvas得动画播放&#xff0c;他们的动画参数是不一样的。一个…
阅读更多...
微服务--服务介绍

微服务--服务介绍

1.2.2 常见微服务架构 1. dubbo: zookeeper dubbo SpringMVC/SpringBoot 配套 通信方式: rpc 注册中心: zookeeper/redis 配置中心: diamond 2.SpringCloud: 全家桶轻松入第三方组件(Netflix) 配套 通信方式: http restful 注册中心: eruka /consul 配置中心: config 断 路器…
阅读更多...
【学习笔记】计算机视觉对比学习综述

【学习笔记】计算机视觉对比学习综述

计算机视觉对比学习综述 前言百花齐放InstDiscInvaSpreadCPCCMC CV双雄MoCoSimCLRMoCo v2SimCLR v2SwAV 不用负样本BYOLSimSiam TransformerMoCo v3DINO 总结参考链接 前言 本篇对比学习综述内容来自于沐神对比学习串讲视频以及其中所提到的论文和博客&#xff0c;对应的链接详…
阅读更多...
Linux学习之权限

Linux学习之权限

在学习Linux权限之前&#xff0c;我们先理解一下关于Linux内核与shell外壳之间的关系&#xff1a; shell命令以及运行原理 Linux严格意义上说的是一个操作系统&#xff0c;我们称之为“核心&#xff08;kernel&#xff09;“ &#xff0c;但我们一般用户&#xff0c;不能直接使…
阅读更多...
Redis笔记——（狂神说）

Redis笔记——（狂神说）

Nosql概述 为什么要用NoSql&#xff1f; 1、单机mysql的年代&#xff1a;90年代&#xff0c;网站访问量小&#xff0c;很多使用静态网页html写的&#xff0c;服务器没压力。 当时瓶颈是&#xff1a;1)数据量太大一个机器放不下。2)数据的索引(BTree)&#xff0c;一个机器内存也…
阅读更多...
Kotlin判断null比较let布尔值Boolean

Kotlin判断null比较let布尔值Boolean

Kotlin判断null比较let布尔值Boolean class MyData {val count: Int? 2023val number: Int? null }fun main(args: Array<String>) {val data MyData()val year 2022if (data.count ! null) {if (data.count > year) {println("data.count ! null")}}…
阅读更多...
一些自用logo

一些自用logo

阅读更多...
【STM32】学习笔记(OLED)-江科大

【STM32】学习笔记(OLED)-江科大

调试方式 OLED简介 硬件电路 驱动函数 OLED.H #ifndef __OLED_H #define __OLED_Hvoid OLED_Init(void); void OLED_Clear(void); void OLED_ShowChar(uint8_t Line, uint8_t Column, char Char); void OLED_ShowString(uint8_t Line, uint8_t Column, char *String); void OL…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023