序言

最近在学习python语言，语言有通用性，此文记录复习动态规划并练习python语言。

动态规划（Dynamic Programming）

动态规划是运筹学的一个分支，是求解决策过程最优化的过程。20世纪50年代初，美国数学家贝尔曼（R.Bellman）等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，从而创立了动态规划。动态规划的应用极其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。

基本思想：将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。

斐波那契数列（Fibonacci sequence）

斐波那契数列，又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称“兔子数列”，其数值为：1、1、2、3、5、8、13、21、34……在数学上，这一数列以如下递推的方法定义：F(0)=1，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）。

先以斐波那契数列为例，了解动态规划。

def fibonacci(num):
    if num == 0:
        return 1
    if num == 1:
        return 1
    return fibonacci(num - 1) + fibonacci(num - 2)


if __name__ == "__main__":
    print(fibonacci(10))

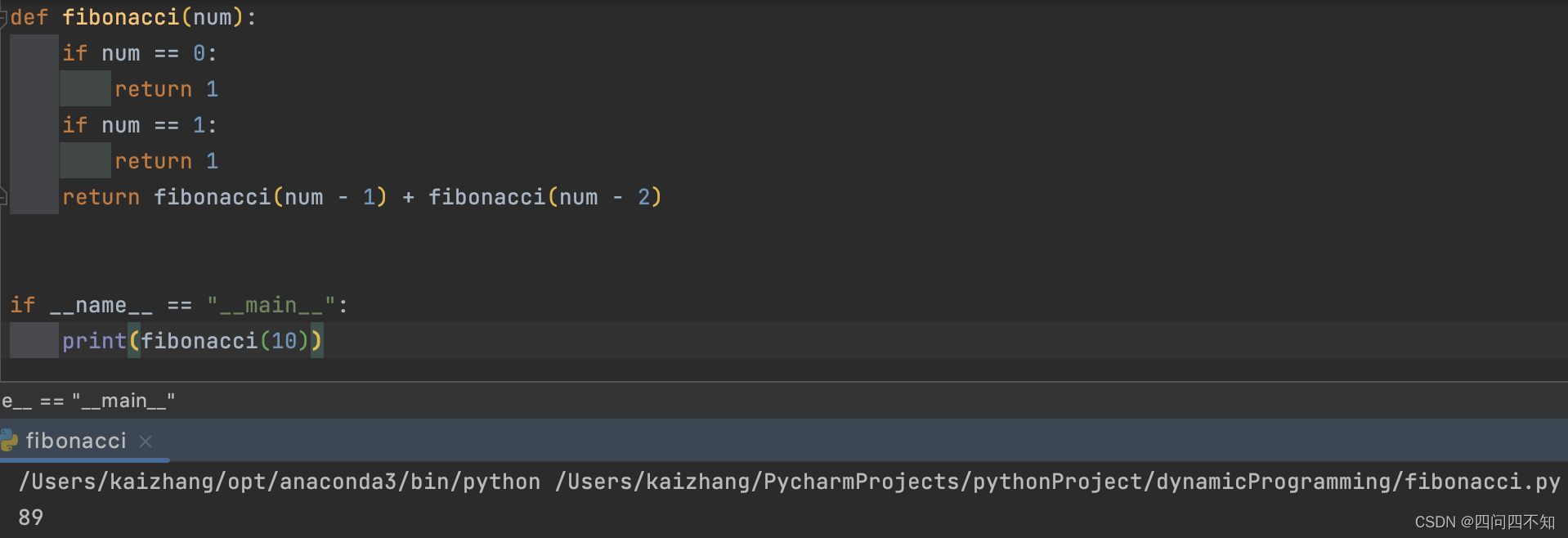
在这里插入图片描述
上述是以递归的方式实现的，然而递归方式存在以下几个缺点：

1）递归调用，占用空间大；
2）递归太深，容易发生栈溢出；
3）可能存在大量重复计算；

结果	（n-1）项	（n-2）项
f(n)	f(n-1)	f(n-2)
…	…	…
f(5)	f(4)	f(3)
f(4)	f(3)	f(2)
f(3)	f(2)	f(1)
f(2)	f(1)	f(0)

以上述表格为例，可以看到在求下一个递归结果时，计算了之前已经计算出来的结果，存在重复计算项。

如果采用动态规划的方式，那么可以节省计算，采用数组暂存之前已经计算出来的结果。如下，

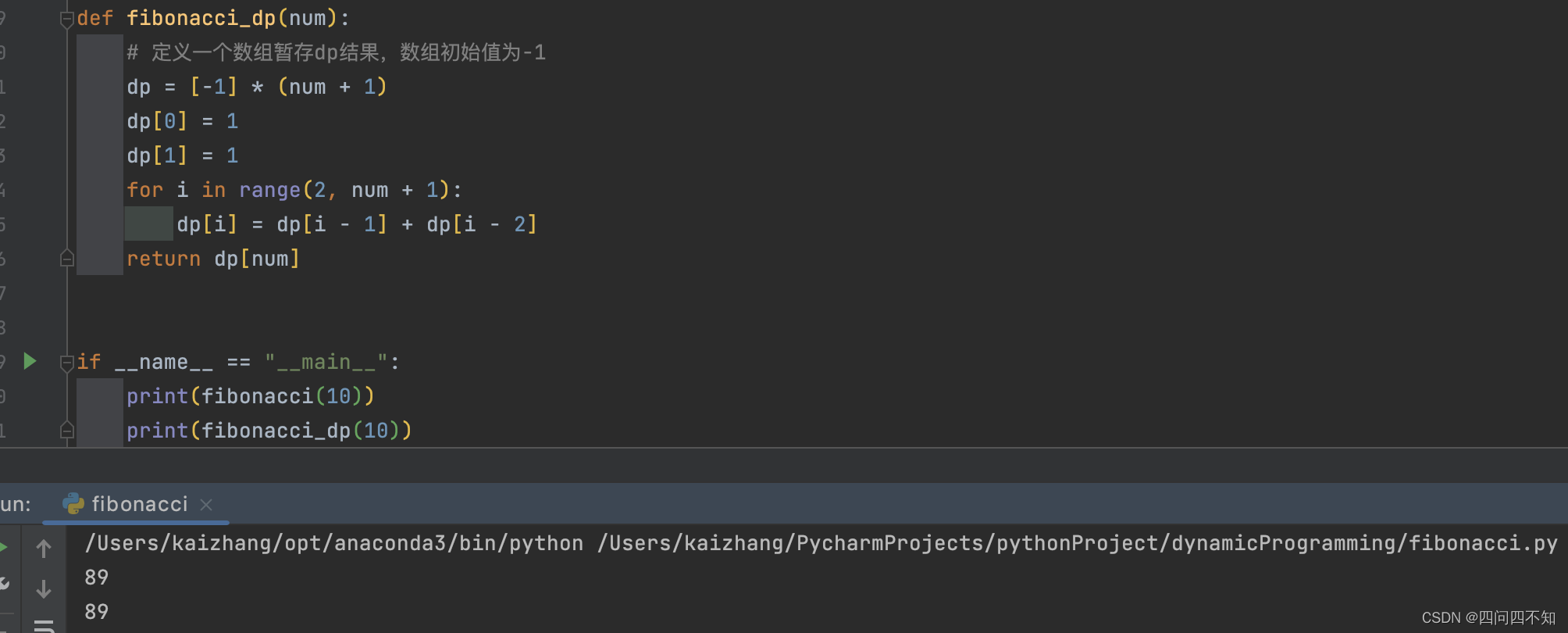
def fibonacci_dp(num):
    # 定义一个数组暂存dp结果，数组初始值为-1
    dp = [-1] * (num + 1)
    dp[0] = 1
    dp[1] = 1
    for i in range(2, num + 1):
        dp[i] = dp[i - 1] + dp[i - 2]
    return dp[num]


if __name__ == "__main__":
    print(fibonacci_dp(10))

在这里插入图片描述

不同路径

上面的斐波那契数列是一维数组，较为简单，下面以二维数组为例。

题目描述

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径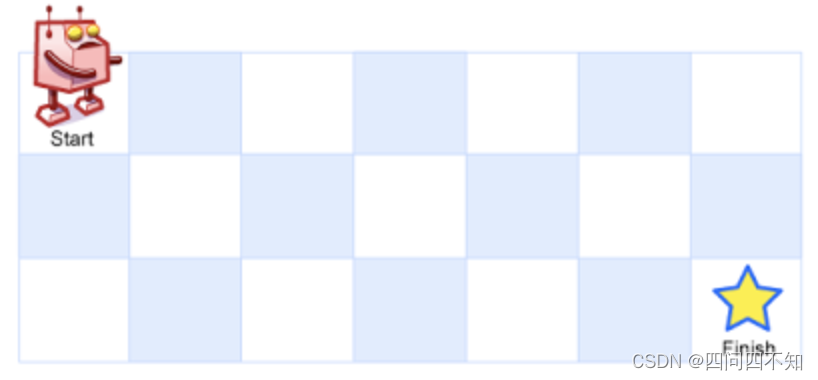？在这里插入图片描述

示例1: 输入：m = 3, n = 7 输出：28

示例2: 输入：m = 3, n = 2 输出：3
解释：从左上角开始，总共有 3 条路径可以到达右下角。
1.向右 -> 向下 -> 向下
2.向下 -> 向下 -> 向右
3.向下 -> 向右 -> 向下
示例3:
输入：m = 7, n = 3 输出：28
示例4:
输入：m = 3, n = 3 输出：6
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9

python代码

class UniquePaths(object):
    def uniquePaths(self, m: int, n: int) -> int:
        """
        :type m: int
        :type n: int
        :rtype: int
        """

        # 初始化一个二维数组
        dp = [[0] * n for _ in range(m)]
        for i in range(m):
            dp[i][0] = 1
        for j in range(n):
            dp[0][j] = 1
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        return dp[m - 1][n - 1]


if __name__ == "__main__":
    demo = UniquePaths()
    print(demo.uniquePaths(7, 3))

在这里插入图片描述

最小路径和

题目描述

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：一个机器人每次只能向下或者向右移动一步。

在这里插入图片描述

示例1：
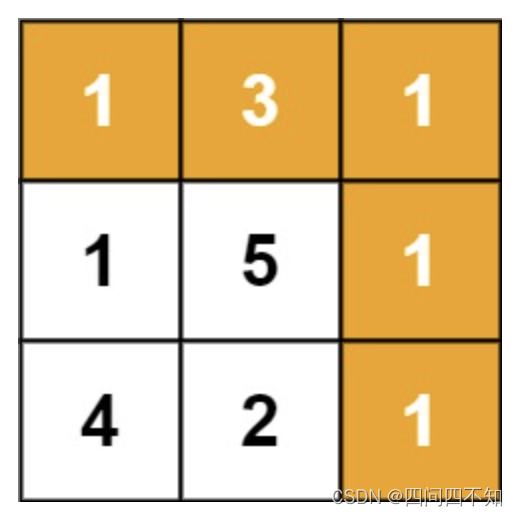
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。
示例2：
输入：grid = [[1,2,3],[4,5,6]]
输出：12
提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

python代码

class MinPathSum(object):
    def minPathSum(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        row = len(grid)
        column = len(grid[0])
        # 定义dp[i][j]为到(i,j)处的最小路径和
        dp = [[0] * column for _ in range(row)]
        dp[0][0] = grid[0][0]
        # 第0行j列
        for j in range(1, column):
            dp[0][j] = dp[0][j - 1] + grid[0][j]
        # 第i行0列
        for i in range(1, row):
            dp[i][0] = dp[i - 1][0] + grid[i][0]
        # 非第0行或第0列
        for i in range(1, row):
            for j in range(1, column):
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
        return dp[row - 1][column - 1]


if __name__ == "__main__":
    demo = MinPathSum()
    grid = [[1, 3, 1], [1, 5, 1], [4, 2, 1]]
    print(demo.minPathSum(grid))