目录

1. 安装git

2. gitbash配置

2.1 设置

2.2 生成key

2.3 初始化本地仓库

 2.4 clone远程仓库的工程到本地

2.5 本地修改提交

---

 

1. 安装git

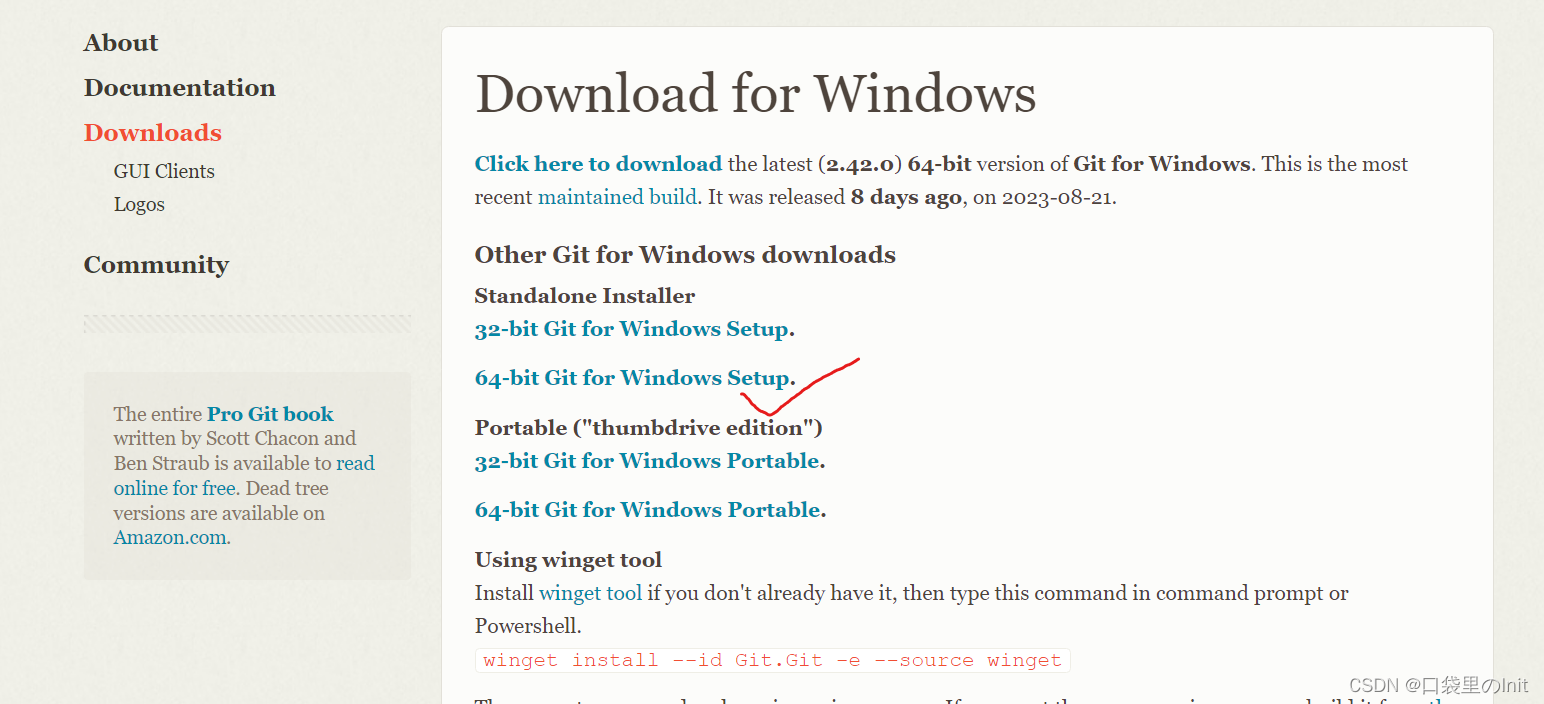
默认安装。

2. gitbash配置

2.1 设置

打开gitbash，设置用户名和邮箱：

git config --global user.name "yourname"
git config --global user.email "xxyyzz@163.com"
git config --global credential.helper store   

• yourname：你注册gitee时的用户名
• xxyyzz@163.com：gitee里面的主邮箱
• 第三句是记住前两句配置

使用如下命令，查看配置结果：

git config --list 

2.2 生成key

输入：

ssh-keygen

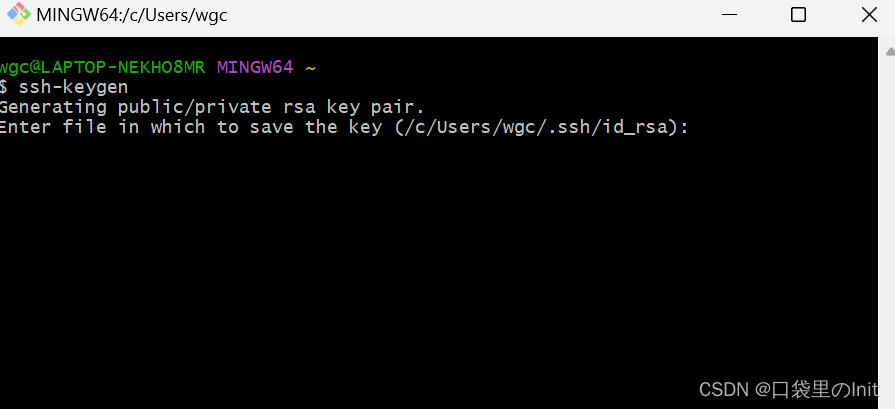 敲3次回车！！！

打开如下目录的 id_rsa.pub ：

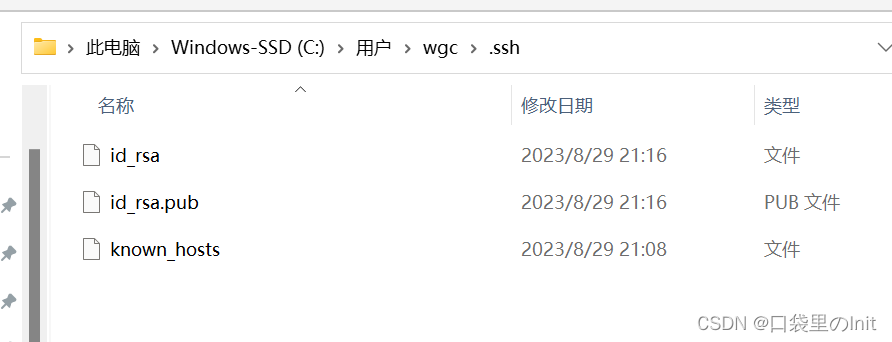
        全选复制。然后打开我们的Gitee，进入设置–>SSH公钥–>在公钥区粘贴我们所copy的公钥，点击确定输入Gitee登陆密码进行验证即可。 

2.3 初始化本地仓库

进入到指定的文件夹之后，使用git init指令将本地文件夹变成本地仓库

git init

 本地文件夹多出一个隐藏文件：

 2.4 clone远程仓库的工程到本地

git clone xxx  // ‘xxx’表示需要克隆的仓库的链接

eg:

git remote add origin https://gitee.com/w-guchao/test.git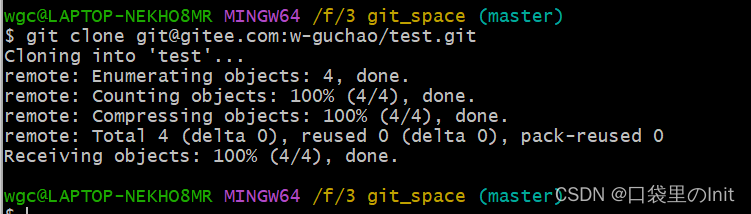

2.5 本地修改提交

git status 

获取状态：

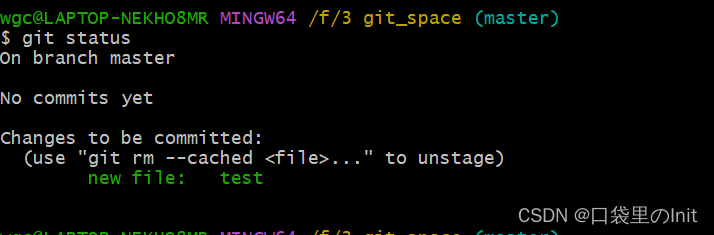
test文件夹内加个文件，再看状态：：

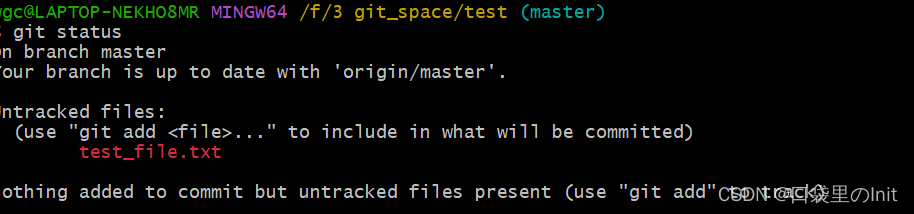
 （1）git add 文件名 表示将某个文件添加至暂存区。

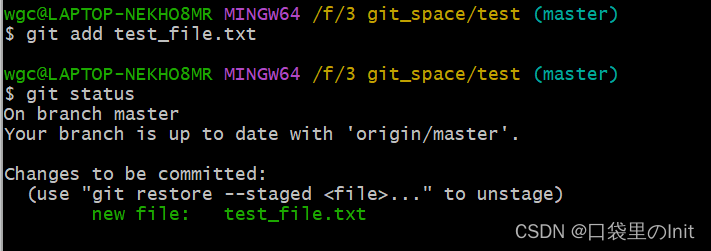
（2）git commit -m “xxx”，  xxx表示自己对本次提交所进行的备注或者标注。 

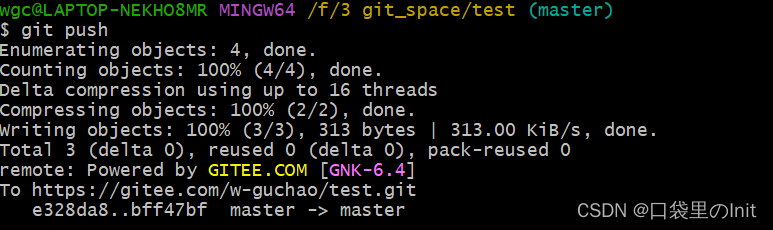
（3）git push 指令提交到服务端。