图片来源：王道数据结构第六章

---

目录

邻接矩阵法

不带权的

带权的图

邻接矩阵法的性能分析

链接 对阵矩阵的压缩存储

邻接矩阵法的性质

邻接表法

链接 树的孩子表示法

性能分析

对比邻接矩阵

十字链表法

性能分析

邻接多重表

邻接多重表存储无向图

四种存储结构的总结

---

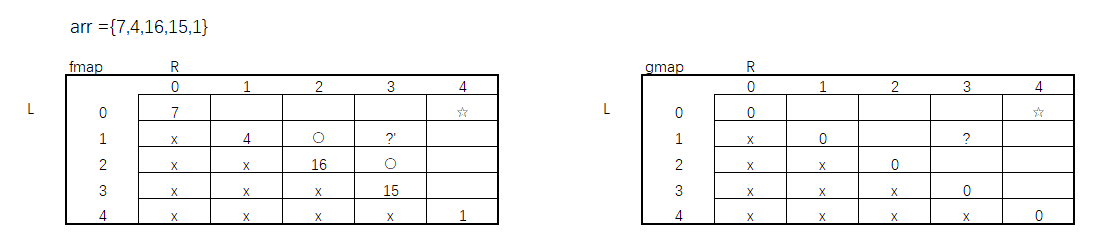
邻接矩阵法

不带权的

其实就是二维数组。

//图的相关代码
#define MaxVertexNum 100 //顶点数目的最大值
typedef struct{
    char Vex[MaxVertexNum];//顶点表
    int Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵，边表
    int vexnum,arcnum;//图的当前顶点数和边数
}MGraph;

里面存储的值，为1就是有边，为0就是没有边。

无向图中：

第i个结点的度=第i行（或者第i列）的非零元素的个数。

有向图中

第i个结点的出度：第i行的非零元素的个数

第i个结点的入度：第i列的非零元素的个数

第i个结点的度=第i行、第i列的非零元素的个数之和

 

要遍历矩阵的一整行或者一整列，所以相当于遍历一遍所有的结点，所以为O(|V|)。

带权的图

 

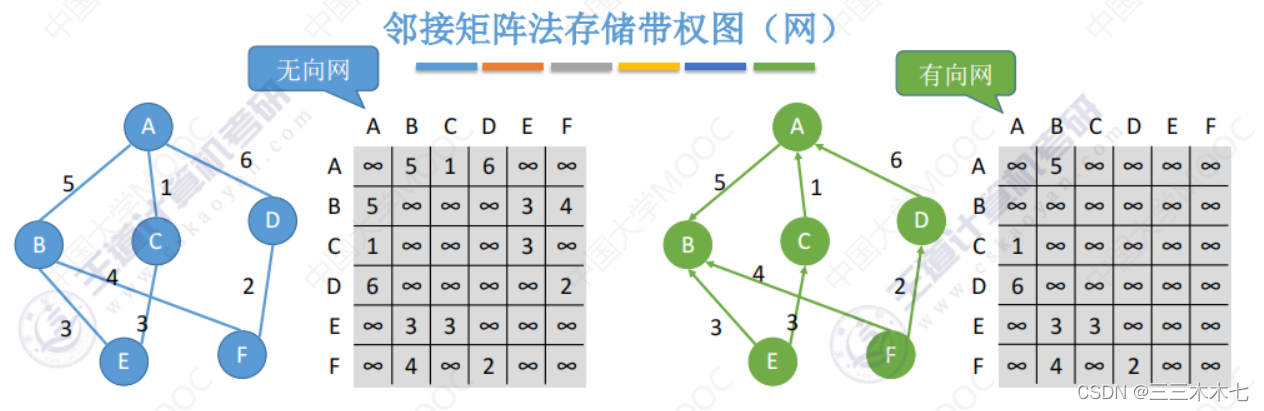
邻接矩阵法的性能分析

链接 对阵矩阵的压缩存储

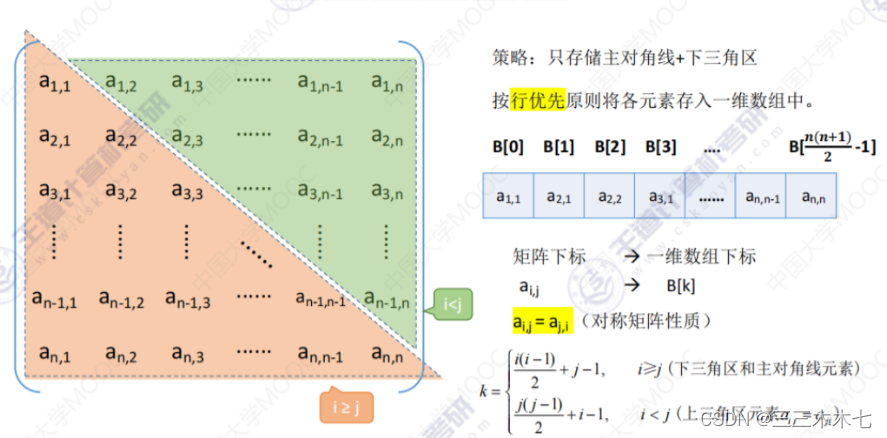
邻接矩阵法的性质

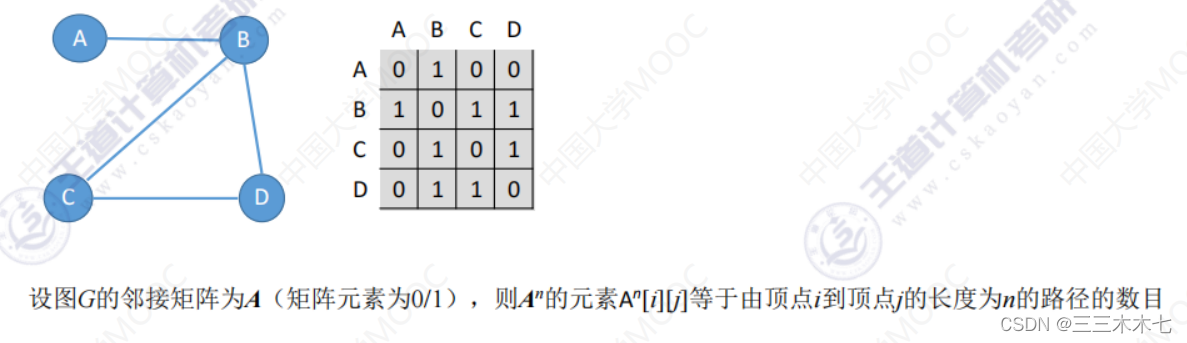
邻接表法

顺序+链式存储

有一个数组，存储顶点，这个顶点是个结点，里面有顶点信息，还有指向第一条边的指针。

然后边的存储也是利用结点，ArcNode，存储了该结点指向的结点的下标（要存储本边指向的是哪个结点）以及指向下一条弧的指针，可能还会有边权值。

 

最后图的存储，利用一个顶点结点们 构成的数组vertices，还存储了顶点和边的数量

 

总结：

1.先写顶点的存储结构 顶点的数值和指向第一条边的指针，这个指针式边类型的指针（要存储本边指向的是哪个结点，还要存储一个指针，指向下一条边）

int data , *first，

2.编写 边类型的结点

要存储本边指向的是哪个结点，还要存储指向下一条边的指针 ，可能还会有边权值。

int index（adjvex），sstruct ArcNode *next

3.最后形成图的存储

AdjList vertices，

链接 树的孩子表示法

 

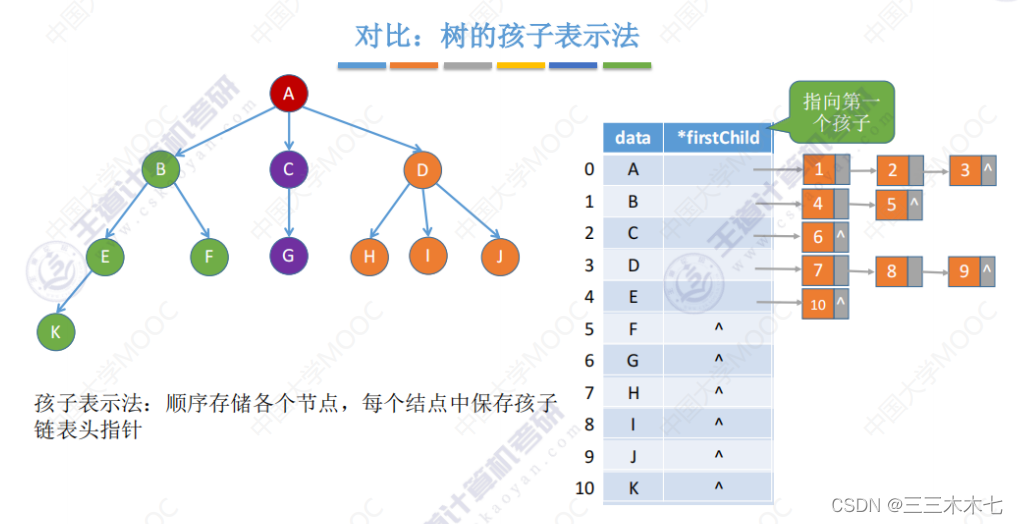
性能分析

无向图：

 

无向图 A-B ，A到B B到A都存储了一遍

有向图：

 

对比邻接矩阵

邻接矩阵：只要确定了顶点编号，图的邻接矩阵表示方法就唯一。

邻接表：图的邻接表的表示方式并不唯一

 

十字链表法

 

首先有一排顶点结点，用数组顺序存储

顶点结点：存储它本身的数据，一个指针这个指针指向该顶点作为弧头的第一条狐（边的终点，可计算这个结点的入度），一个指针这个指针指向该顶点作为狐尾的第一条弧（边的起点，可计算这个结点的出度）

 

弧结点

 

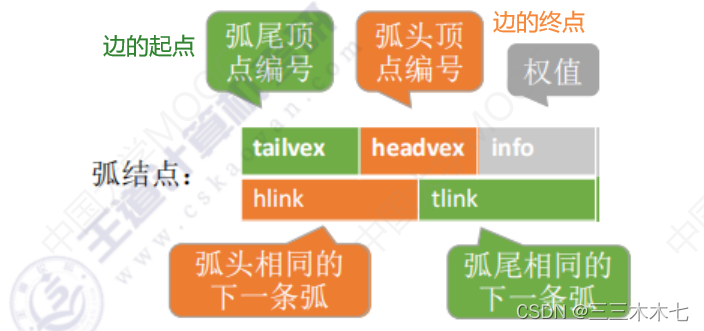
性能分析

 

邻接多重表

邻接矩阵存储无向图：空间复杂度高

邻接表存储无向图：两条边对应两份冗余信息，删除顶点、删除边等操作，时间复杂度高

邻接多重表存储无向图

顶点结点：数据据，一个指针指向与该顶点相连的第一条边

边结点：存储边的两个顶点编号i j 可能还有权值，一个指针指向依附于顶点i的下一条边，一个指针指向依附于顶点j 的下一条边

 

四种存储结构的总结