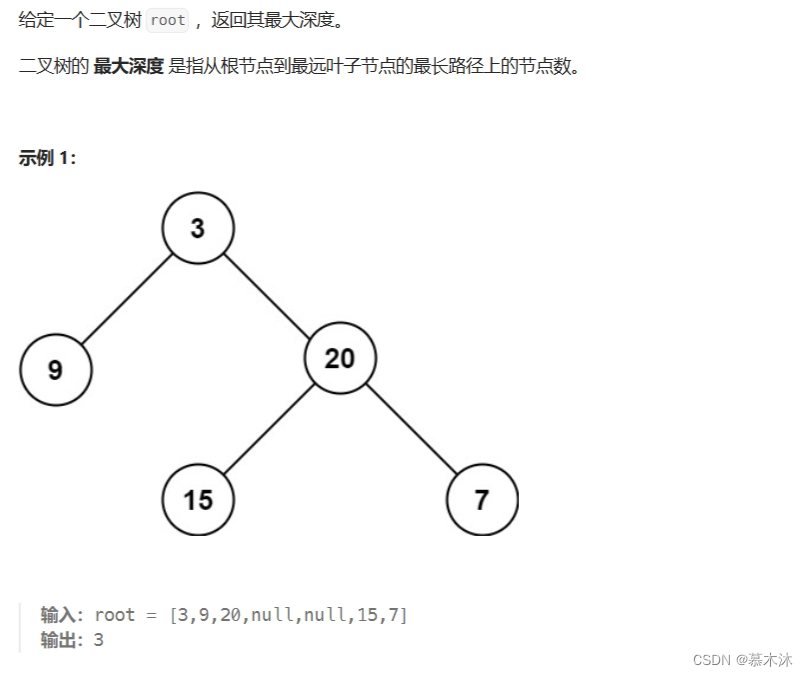
1.最大深度问题
思路:递归三部曲
第一步:确定参数和返回值
题目要求求二叉树的深度,也就是有多少层,需要传递一个root从底层向上统计
int maxDepth(TreeNode root)
第二步:确定终止条件
当递归到null时就说明到底了,返回0
第三步:确定单层逻辑
一个结点的深度=max(左,右)+1
class Solution {
public int maxDepth(TreeNode root) {
if( root== null){
return 0;
}
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return 1+Math.max(left,right);
}
}2.判断平衡二叉树
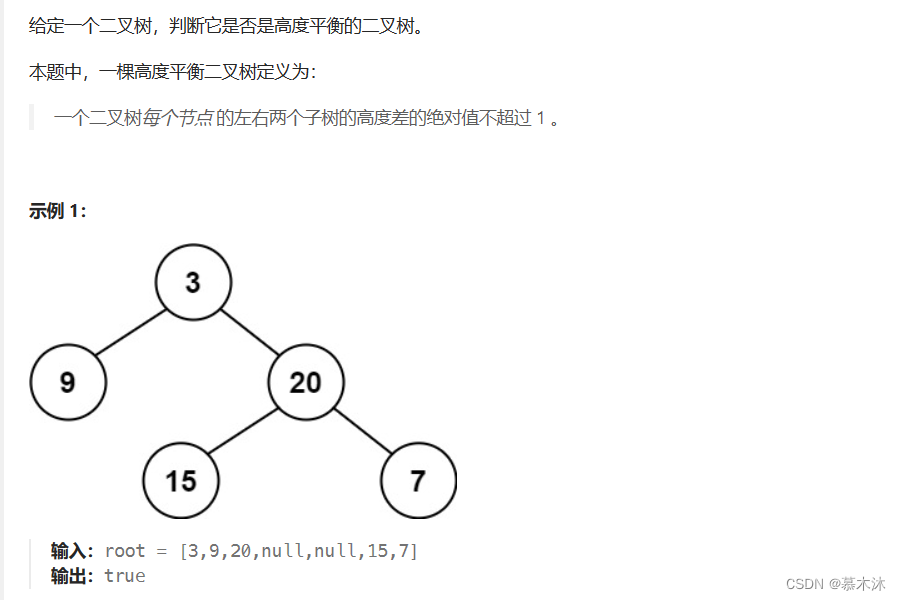
思路:递归三部曲
第一步:确定参数和返回值
从底向上统计结点高度,int trace(TreeNode root)
第二步:确定终止条件
当递归到空代表触底,当左右结点高度差大于1代表失败直接一路返回-1
否则就是继续向下
第三步:确定单层逻辑
判断有无不平衡现象出现,若无往上返回一层将结点高度+1
class Solution {
public boolean isBalanced(TreeNode root) {
return trace(root)>-1;
}
public int trace(TreeNode root){
if(root == null){
return 0;
}
int left = trace(root.left);
int right = trace(root.right);
if(left == -1 || right == -1 || Math.abs(left - right)>1){
return -1;
}
return 1+Math.max(left,right);
}
}3.最小深度
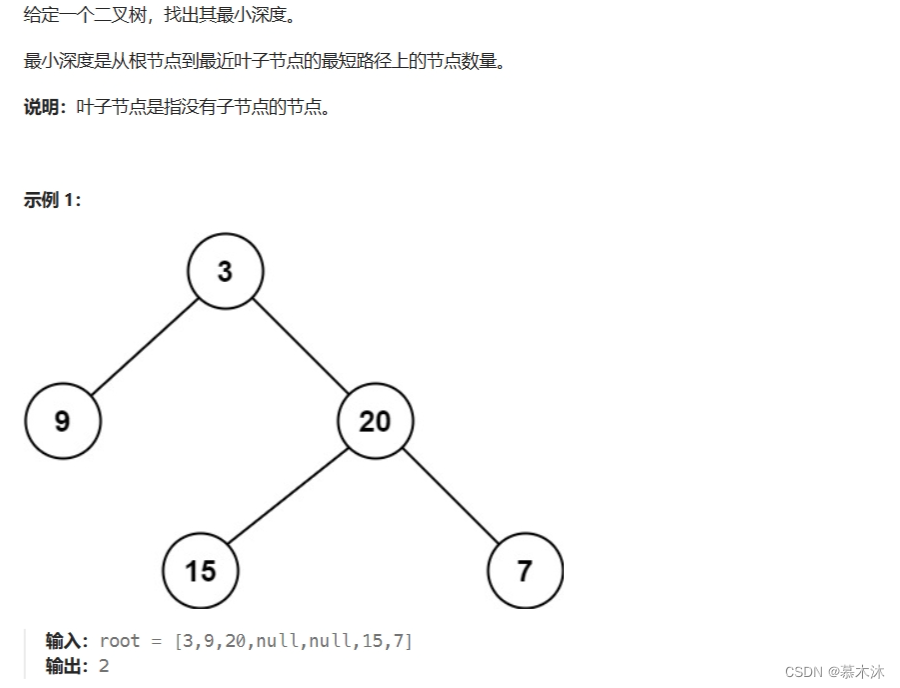
思路:递归三部曲
第一步:确定参数和返回值
还是需要遍历结点求深度,需要传入结点返回深度值
int trace(TreeNode root)
第二步:确定终止条件
当遍历到空时就返回0
第三步: 确定单层逻辑
需要注意的是根结点深度为1但不能算到最小深度,如果直接返回1+Min(左,右)就不符合条件
这样就需要避免根结点某一孩子为空情况
- 左结点为空右结点不为空时,返回右结点深度+1
- 右结点为空左结点不为空时,返回左结点深度+1
- 如果都不为空就返回1+Min(左,右)
class Solution {
public int minDepth(TreeNode root) {
return trace(root);
}
public int trace(TreeNode root){
if(root == null){
return 0;
}
int left = trace(root.left);
int right = trace(root.right);
if(root.left==null){
return right+1;
}
if(root.right==null){
return left + 1;
}
return 1+Math.min(left,right);
}
}4.N叉树的最大深度
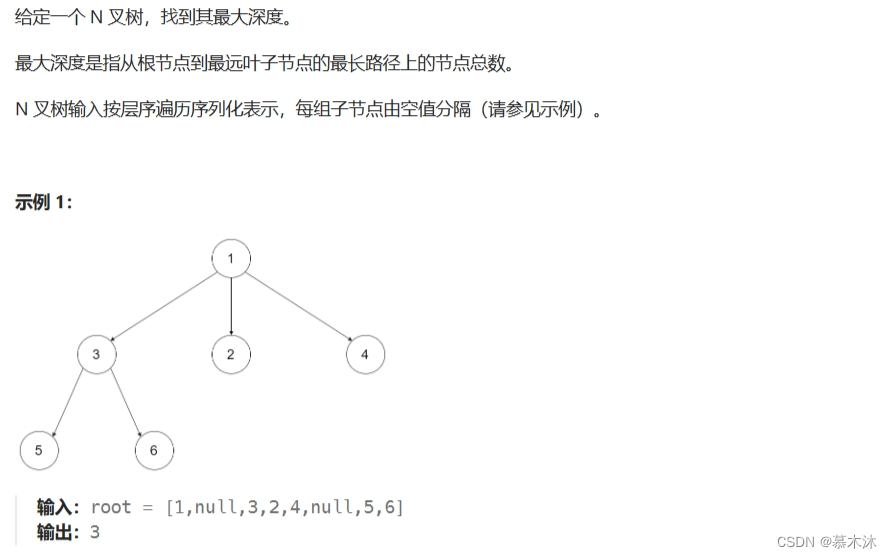
思路:递归三部曲
第一步:确定参数和返回值
此题也是求树的深度需要遍历结点,传入结点返回深度值
第二步:确定终止条件
当结点为空返回深度0,当孩子为空返回1,其他就遍历孩子列表挨个求出最大深度
第三步:确定单层逻辑
保存孩子的深度,取最大值
class Solution {
public int maxDepth(Node root) {
if(root == null){
return 0;
}
if(root.children.isEmpty()){
return 1;
}
List<Integer> list = new ArrayList<>();
for(Node node : root.children){
int res = maxDepth(node);
list.add(res);
}
int max = 0;
for(int num : list){
if(num > max){
max = num;
}
}
return 1 + max;
}
}





![[Unity]UI和美术出图效果不一致](https://img-blog.csdnimg.cn/e27e9b850495476d931e7cc785cf9d1d.webp)




![后端Windows软件环境安装配置大全[JDK、Redis、RedisDesktopManager、Mysql、navicat、VMWare、finalshell、MongoDB...持续更新中]](https://img-blog.csdnimg.cn/913823bfa11a480697c1f4049df15214.png)