复杂度分析

news2025/1/12 20:49:02

算法

如何评估一个算法的好坏？(事后统计法的应用)

在同一个问题上比较不同算法对于同一输入的执行时间

事后统计法的缺点

1.严重依赖硬件以及运行时各种不确定因素(比如cpu好一点的效率就高一点)

2.必须编写相应的测试代码

3.测试时输入的数据难以保证公平性(比如你输入20时第一台主机效率高一点第二台主机效率第一点当你输入40时第一台主机效率低一点第二台主机效率高一点)

事后统计法的优化

为了弥补事后统计法的缺点我们可以通过一下这三个维度去评估算法的好坏：

1.正确性(编写代码时代码写的正不正确)、可读性(比如可以多行书写的代码开发人员却写成了一整行导致用户的观感变差)、健壮性(对不合理的输入进行判断并且做出处理)

2.时间复杂度(计算代码执行所需要的时间)

3.空间复杂度(计算代码占用所需要的内存空间)

大O表示法

大O表示法是对复杂度的估算用于描述复杂度

大O表示法的原则：保留最高阶、舍弃较低阶以及最高阶的系数

对数阶的细节

众所周知：log2(n) = log2(3) * log3(n)

所以我们可以知道一个对数等于一个常数乘以一个对数

所以我们对于对数可以简化成O(logn)

大O表示法实例一

public void test1(int n){
    // 以下是一个多重if语句的实例
    // 由于多重if语句属于互斥事件 所以只会执行一次 所以用大O表示法表示为O(1)
    if(n > 10){
        System.out.println("n>10");
    }else if(n > 5){
        System.out.println("n>5");
    }else{
        System.out.println("n<=5");
    }
    // 以下是一个for循环的案例
    // 针对for循环 执行次数是这样算的 包括初始化语句、条件判断语句、条件控制语句、循环体语句 其中条件判断语句=条件控制语句=循环体语句 所以执行次数等于1+4+4+4=13次 用大O表示法表示为O(1)
    for(int i = 0; i < 4; i++){
        System.out.println("test");
    }
}

大O表示法实例二

public void test2(int n){
    // 以下还是一个for循环案例 只不过是把案例一的4换成了n而已 目的在于让for循环的复杂度变得通用
    // 根据案例一的分析 我们可以知道执行次数一共为1+3n 用大O表示法表示为O(n)
    for(int i = 0; i < n; i++){
        System.out.println("test");
    }
}

大O表示法实例三

public void test3(int n){
    // 以下是嵌套for循环案例 执行次数为1+2n+n(1+3n)=3n^2+3n+1 用大O表示法表示为O(n^2)
    for(int i = 0; i < n; i++){
        for(int j = 0; j < n; j++){
            System.out.println("test");
        }   
    }
}

大O表示法实例四

public void test4(int n){
    // 以下是嵌套for循环的案例 只不过把内层循环的条件判断语句换成了非变量而已 那么这下子的执行次数即为1+2n+n(1+3*15)=1+48n 用大O表示法表示为O(n)
    for(int i = 0; i < n; i++){
        for(int j = 0; j < 15; j++){
            System.out.println("test");
        }
    }
}

大O表示法案例五

public void test5(int n){
    // 以下是while循环的案例 我们可以通过举例子的形式来帮助大家理解
    // 假设n=8 第一次执行时n为4 第二次执行时n为2 第三次执行时n为1 一共执行了3次 即为log2(8)次 有根据对数阶的规则我们可以知道用大O表示法表示为O(logn) 而且while循环执行次数一般不把条件判断语句算入其中 只把循环体语句算入其中
    while((n = n / 2) > 0){
        System.out.println("test");
    }
}

大O表示法案例六

public void test6(int n){
    // 以下案例是while循环 假设n=25 当n=5时 为第一次执行次数 当n=1时 为第二次执行次数 所以一共有2次执行次数 即为log5n次 用大O表示法表示为O(logn)
    while((n = n / 5) > 0){
        System.out.println("test");
    }
}

大O表示法案例七

public void test7(int n){
    // 以下是嵌套for循环 综上几个案例所述  我们可以知道这个嵌套循环的执行次数为1+2log2n+log2n*(1+3n) 化简后为3nlog2n+3log2n+1 用大O表示法表示为O(nlogn)
    for(int i = 1; i < n; i = i * 2){
        for(int j = 0; j < n; j++){
            System.out.println("test");
        }
    }
}

大O表示法案例八

public void test8(int n){
    // 以下是空间复杂度的案例 变量a、b、c分别占用3个内存空间 而array数组则是开辟了n个内存空间 所以一共开辟了n+3个内存空间 用大O表示法表示为O(n)    
    int a = 10;
    int b = 20;
    int c = a + b;
    int[] array = new int[n];
    for(int i = 0; i < array.length; i++){
        System.out.println(array[i]);
    }
}

大O表示法案例九

public void test9(int n, int k){
    // 以下案例时针对多个数据规模进行的 所以用大O表示法表示为O(n + k)
    for(int i = 0; i < n; i++){
        System.out.println("test");
    }
    for(int j = 0; j < k; j++){
        System.out.println("test");
    }
}

算法的优化方向

1.用尽量少的空间

2.用尽量少的时间

3.用时间换空间或者用空间换时间

复杂度

复杂度的大小比较

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

复杂度的大小比较(数据规模较小时结合图像分析)

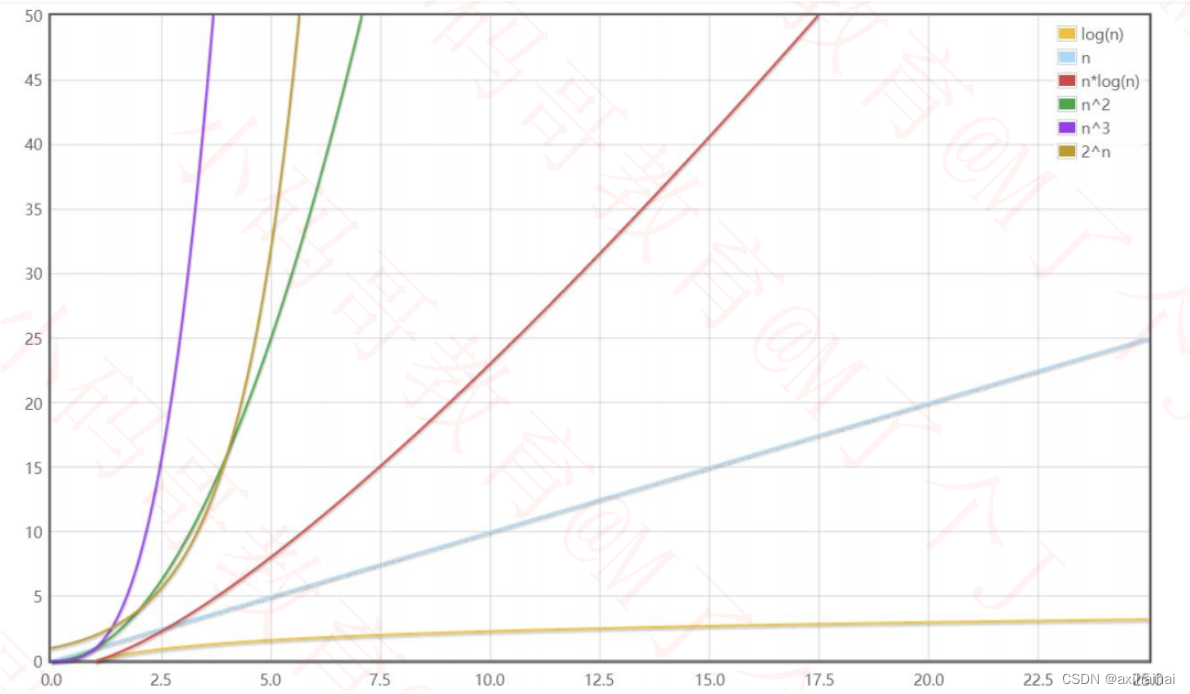
复杂度的大小比较(数据规模较大时结合图像分析)

斐波拉契数列的代码实现

递归算法

public int fib1(int n){
    // 分类讨论 分成n<=1和n>1两种情况
    if(n <= 1)return n;
    return fib1(n - 1) + fib1(n - 2);
}

复杂度分析

当我们的输入为5时

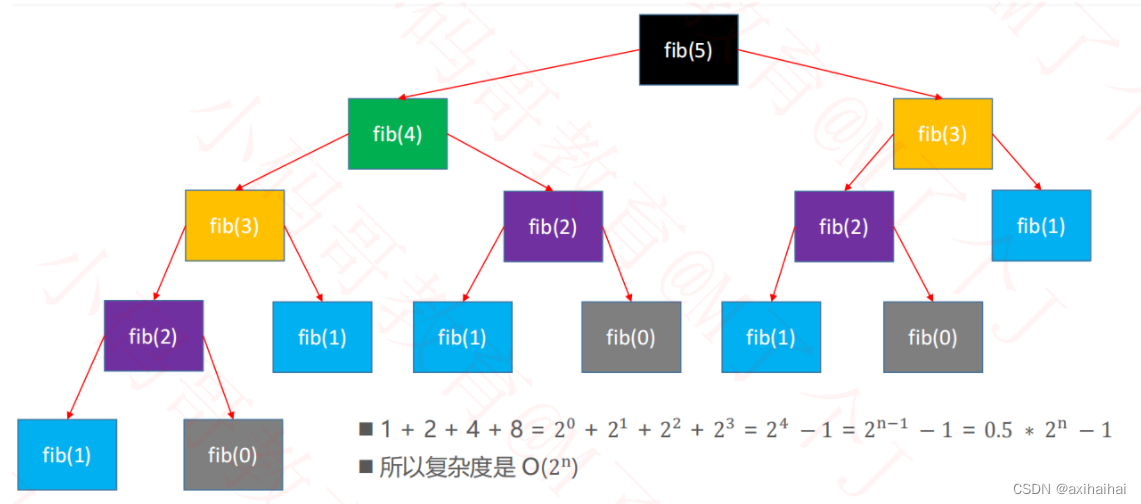
那么用大O表示法表示为O(2^n) 但是0.5*2^n - 1并不是适用于所有的输入

当我们的输入为6时

这个时候总的执行次数为2^(n - 1) - 7 也就是0.5*2^n - 7 所以用大O表示法表示为O(2^n)

非递归实现

public int fib2(int n){
    // 索引 0 1 2 3 4 5 6
    // 菲薄 0 1 1 2 3 5 8
    // 次数     1 2 3 4 5
    // 结论 运算次数 = 索引 - 1
    // 我们可以根据输入进行分类讨论
    if(n <= 1)return n;
    int first = 0;
    int second = 1;
    for(int i = 0; i < n - 1; i++){
        int sum = first + second;
        // 为两个变量重新赋值 但是切记两者顺序不能调换
        first = second;
        second = sum;
    }
    return second;
}

非递归优化实现

public int fib3(int n){
    // 这是斐波拉契数列非递归算法的优化实现 体现在了for循环循环体内部
    if(n <= 1)return n;
    int first = 0;
    int second = 1;
    while((n--) > 1){
        int sum = first + second;
        second += first;
        first = second - first;
    }
}