一.本次需求背景

本文主题：招聘网站的职位招聘数据的分位数图、分位数-分位数图以及散点图、使用线性回归算法拟合散点图处理详解

之前的文章我们已经对爬取的数据做了清洗处理，然后又对其数据做了一个薪资数据的倾斜情况以及盒图离群点的探究。

我们这次的需求是：

使用散点图、使用线性回归算法拟合散点图处理数据 使用局部回归（Loess）曲线（增加一条光滑曲线到散布图）方法处理数据

技术要点：爬虫库（Beautifulsoup、requests-html、Scrapy）、数据预处理（python、kettle）、数据可视化（matplotlib、pyecharts、tebleau）、python-web框架（Flask）

二.职位招聘数据的分位数图、分位数-分位数图

我们这次先看一下效果图：本次任务最后的效果就是下面这俩个图：

1.这块与上面几篇都一样：

使用关键词“java”对数据进行筛选，循环筛选过程中将职位名，薪资需要的关键字放到列表里面，然后存入字典里，经过pandas的处理： 将上限和下限分别处理：

xingzhi={}
zhiwei =[]
xin1 = []
xin2 =[]
for i in range(len(data)):
    if "java" in data.iloc[i]['职位名']:
        a = re.findall("\d+.?\d*", data.iloc[i]['薪资'])
        # print(data.iloc[i]['职位名'])
        zhiwei.append(data.iloc[i]['职位名'])
        xin1.append(int(a[0]))
        xin2.append(int(a[1]))
xingzhi={"职位名":zhiwei,'最低薪资':xin1,'最高薪资':xin2}
df = pd.DataFrame(xingzhi)
java_min=xin1
java_max=xin2
​

2.开始画图：将java数据的上限和下限分别作为两个特征值，传入进行绘图工作：

这里注意一点，我们在进行绘图之前需要使用sort对数据进行一个排序操作。X轴是公司个数，Y轴是薪资,单位K：

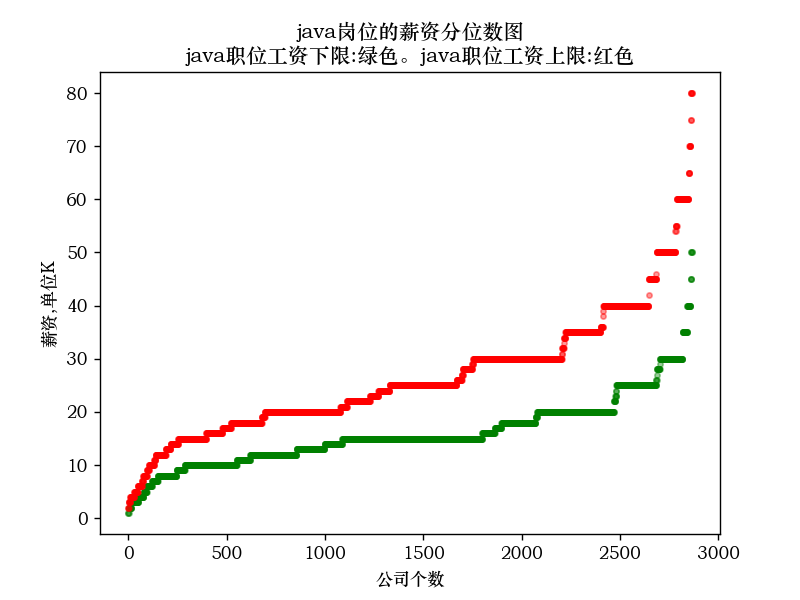
java岗位的薪资分位数图 java职位工资下限:绿色。java职位工资上限:红色

x=range(0, df['最高薪资'].count())
y=np.sort(xin1)
y1=np.sort(xin2)
plt.scatter(x,y,marker='.', c='green',alpha=0.4,label='bulge')
plt.scatter(x,y1,marker='.',c='red',alpha=0.4, label='scratch')
plt.xlabel('公司个数')
plt.ylabel('薪资,单位K')
plt.title('java岗位的薪资分位数图\njava职位工资下限:绿色。java职位工资上限:红色')
plt.show()

3.绘图效果如下：

java岗位的薪资分位数图

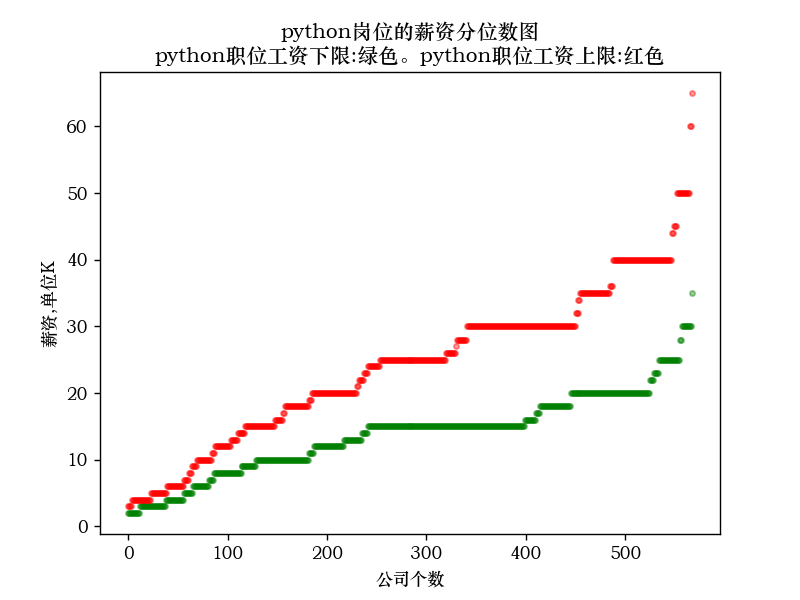
Python岗位的薪资分位数图

Go岗位的薪资分位数图

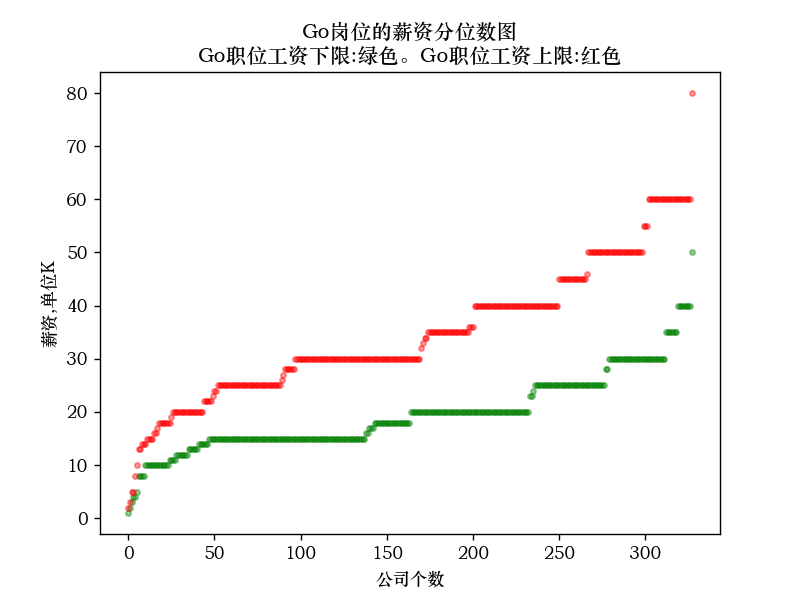
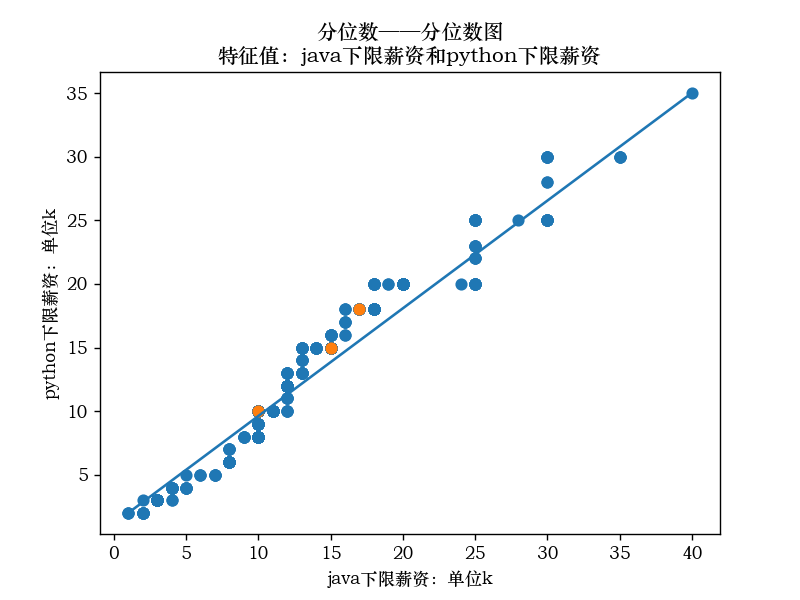
5.分位数—分位数图： 因为java岗位的数据远远的大于Python岗位的数据，我这里的想法是将java岗位的下限和上限分别和Python岗位的下限和上限做为特征值，进行绘图工作。 下限代码如下：

分位数——分位数图

特征值：java下限薪资和python下限薪资:

ava_min=java_min[:len(python_min)]
y=np.sort(java_min)
y1=np.sort(python_min)
​
plt.scatter(y,y1)
plt.plot([y[0],y[-1]],[y1[0],y1[-1]])
plt.scatter([np.quantile(y,0.25),np.quantile(y,0.5),np.quantile(y,0.75)],[np.quantile(y1,0.25),np.quantile(y1,0.5),np.quantile(y1,0.75)])
plt.xlabel('java下限薪资：单位k')
plt.ylabel('python下限薪资：单位k')
plt.title('分位数——分位数图\n特征值：java下限薪资和python下限薪资')
plt.show()

上限代码如下：:

分位数——分位数图

特征值：java上限薪资和python上限薪资

java_max=java_min[:len(python_max)]
y=np.sort(java_max)
y1=np.sort(python_max)
​
plt.scatter(y,y1)
plt.plot([y[0],y[-1]],[y1[0],y1[-1]])
plt.scatter([np.quantile(y,0.25),np.quantile(y,0.5),np.quantile(y,0.75)],[np.quantile(y1,0.25),np.quantile(y1,0.5),np.quantile(y1,0.75)])
plt.xlabel('java上限薪资：单位k')
plt.ylabel('python上限薪资：单位k')
plt.title('分位数——分位数图\n特征值：java上限薪资和python上限薪资')
plt.show()

6.分位数—分位数图效果图如下：

java薪资下限和Python薪资下限的分位数-分位数图:

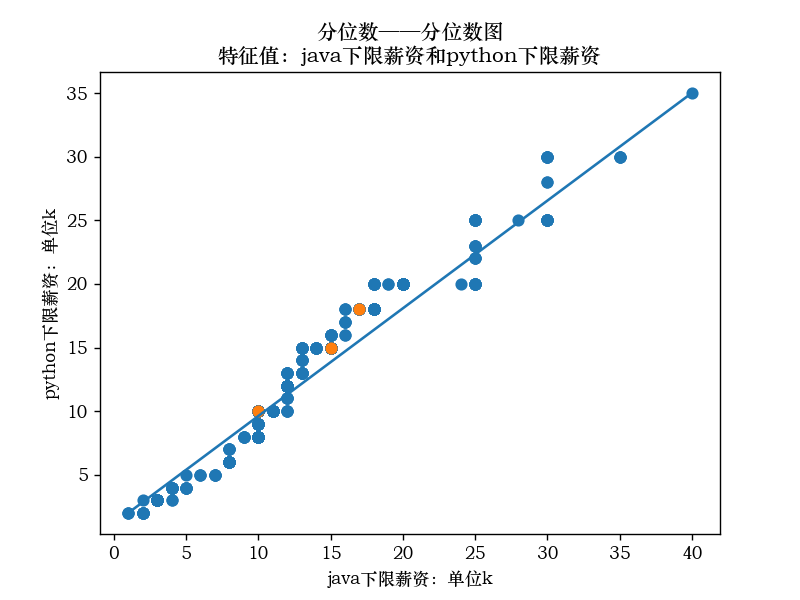
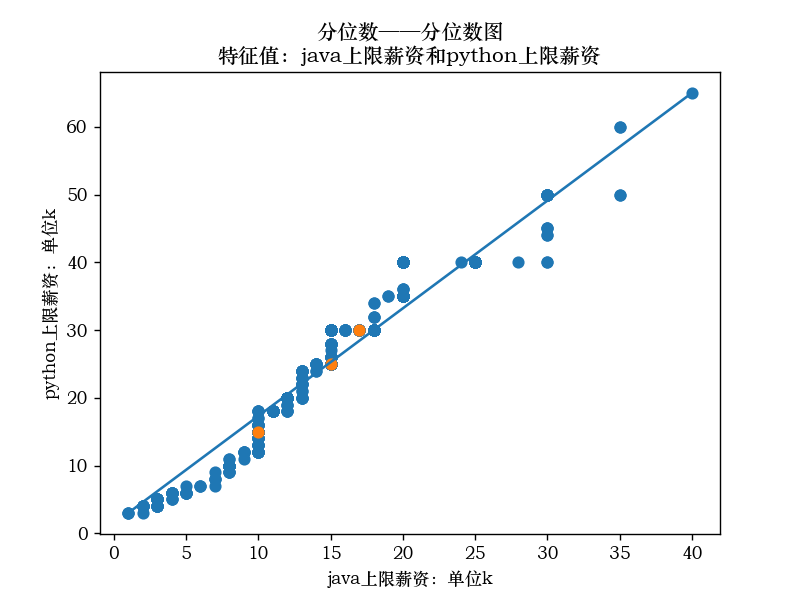
java薪资上限和Python薪资上限的分位数-分位数图

三.使用散点图、使用线性回归算法拟合散点图处理数据

注意：Linear Regression

线性回归算法：线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。 其表达形式为y = w’x+e，e为误差服从均值为0的正态分布。

线性回归算法模型非常简单。每个数据有n个特征，每个特征对应于其自身的权重值。权重加上偏移值的乘积就是线性回归模型。公式如下：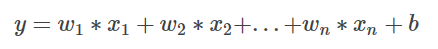

公式如下：

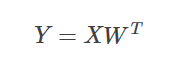
在回归分析中，只包括一个自变量和一个因变量，它们的关系可以近似地用一条直线表示。这种回归分析称为线性回归分析。如果回归分析包括两个或多个自变量，且因变量和自变量之间的关系是线性的，则称为多元线性回归分析。

1.与上文一样，我们使用关键词“java”对数据进行筛选，循环筛选过程中将职位名，薪资需要的关键字放到列表里面，然后存入字典里，经过pandas的处理： 将上限和下限分别处理：

xingzhi={}
zhiwei = []
xin1 = []
xin2 =[]
for i in range(len(data)):
    if "java" in data.iloc[i]['职位名']:
        a = re.findall("\d+.?\d*", data.iloc[i]['薪资'])
        # print(data.iloc[i]['职位名'])
        zhiwei.append(data.iloc[i]['职位名'])
        xin1.append(int(a[0]))
        xin2.append(int(a[1]))
xingzhi={"职位名":zhiwei,'最低薪资':xin1,'最高薪资':xin2}
df = pd.DataFrame(xingzhi)
java1=xin1
java2=xin2

2.使用上面的列表数据进行绘图—散点图:

X轴：各岗位薪资下限，y轴：各岗位薪资上限

plt.scatter(java1,java2, c="red", marker='o', label='java')
plt.scatter(python1,python2, c="green", marker='+', label='python')
plt.scatter(go1,go2, c="yellow", marker='^', label='go')
plt.xlabel('各岗位薪资下限')
plt.ylabel('各岗位薪资上限')
plt.legend(loc=2)
plt.show()

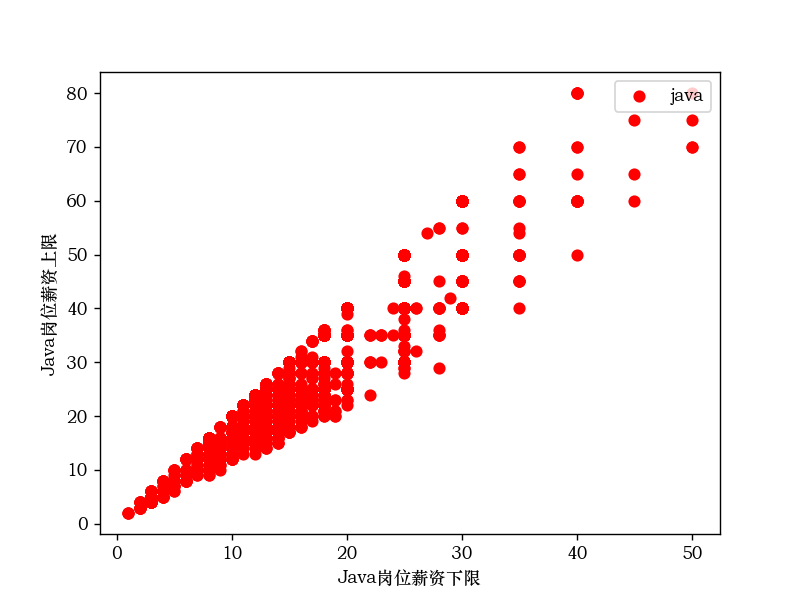
以java为例，其他的俩种语言类似：

plt.scatter(java1,java2, c="red", marker='o', label='java')
plt.xlabel('Java岗位薪资下限')
plt.ylabel('Java岗位薪资上限')
plt.legend(loc=1)
plt.show()

3，效果图如下：

各岗位薪资的的下限和上限散点图：

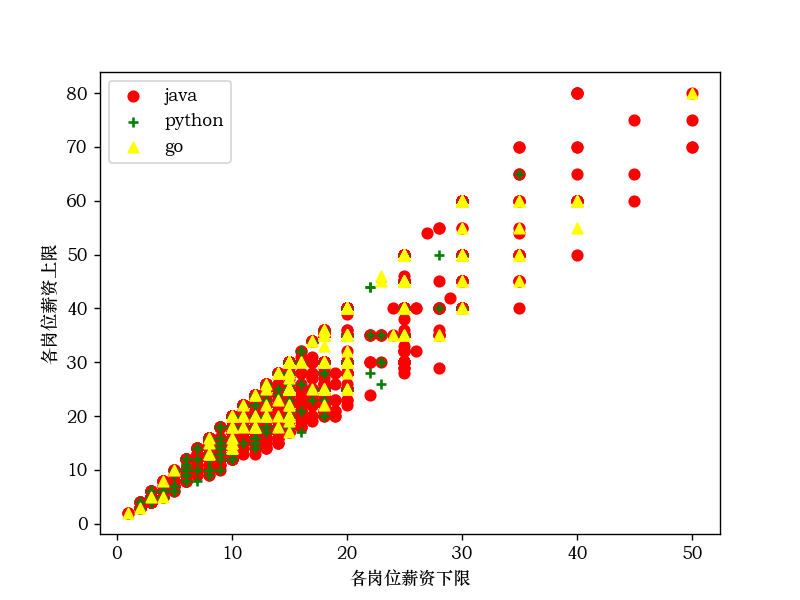
java岗位薪资的的下限和上限散点图：

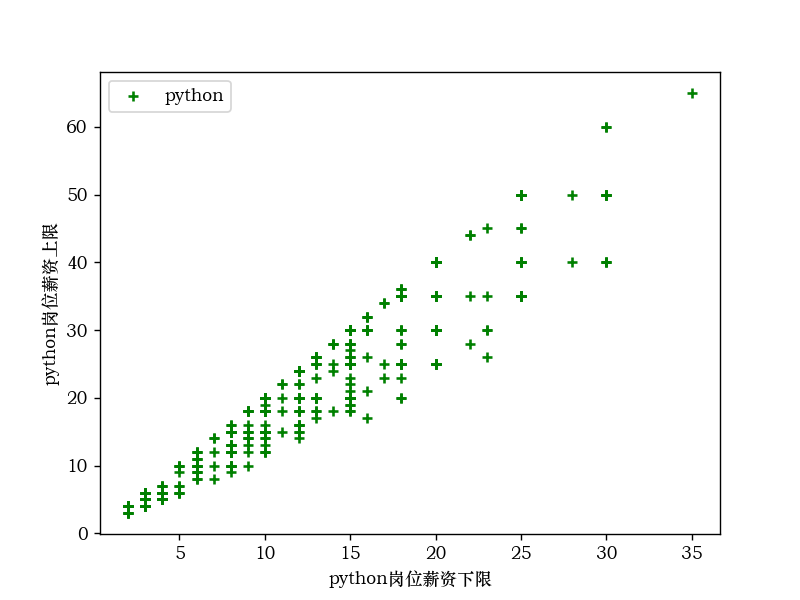
Python岗位薪资的的下限和上限散点图

Go岗位薪资的的下限和上限散点图

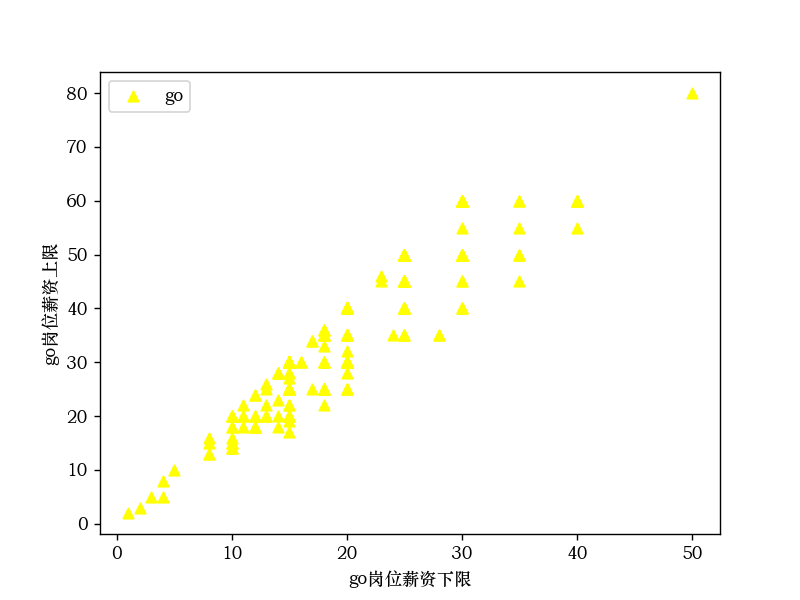
4.使用线性回归算法拟合散点图 使用线性回归算法进行计算，拟合值。

from sklearn import linear_model
linear=linear_model.LinearRegression()
linear.fit(np.reshape(java1,(-1, 1)),np.reshape(java2,(-1, 1)))
print("training score",linear.score(np.reshape(java1,(-1, 1)),np.reshape(java2,(-1, 1))))

5.对其拟合结果进行绘图

X轴：java岗位薪资下限 y轴：java岗位薪资上限

使用线性回归算法拟合散点图

特征值：java岗位薪资下限和java岗位薪资上限

import matplotlib.pyplot as plt
import numpy as np
plt.scatter(np.reshape(java1,(-1, 1)),np.reshape(java2,(-1, 1)),color="red")
plt.scatter(np.reshape(java1,(-1, 1)),np.reshape(java2,(-1, 1)))
plt.scatter(np.reshape(java1,(-1, 1)),np.dot(np.reshape(java1,(-1, 1)),linear.coef_)+linear.intercept_)
plt.xlabel('java岗位薪资下限')
plt.ylabel('java岗位薪资上限')
plt.title("使用线性回归算法拟合散点图\n特征值：java岗位薪资下限和java岗位薪资上限")
plt.show()

6.效果图如下：

java岗位薪资的的下限和上限的线性拟合散点图

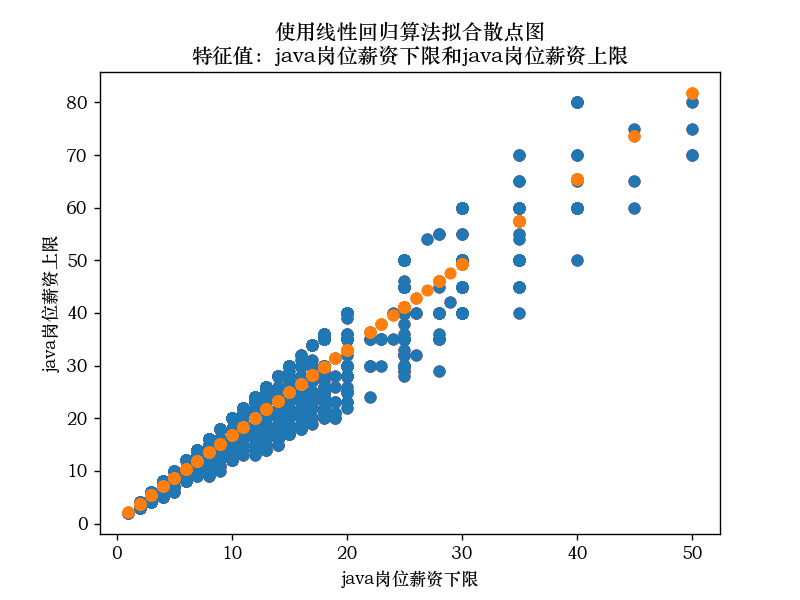
Python岗位薪资的的下限和上限的线性拟合散点图：

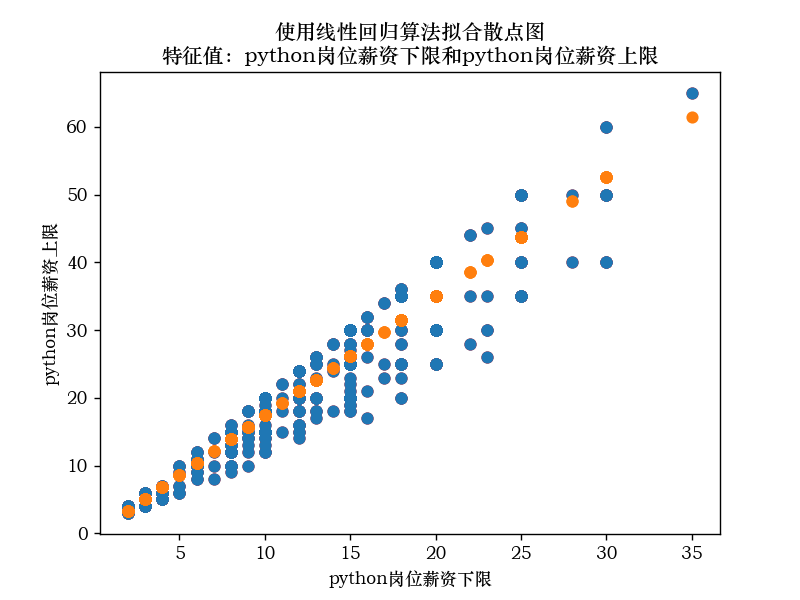
Go岗位薪资的的下限和上限的线性拟合散点图

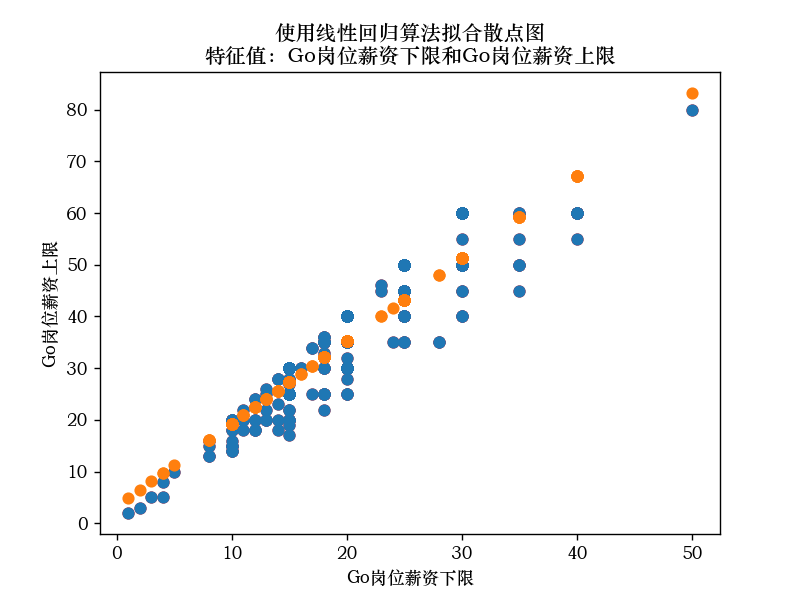
总结：

体会从需求出发，到设计、编码、测试、发布的整体流程，熟悉软件开发过程。熟悉和掌握数据预处理流程。能够在实际中运用数据清理、数据集成、数据变换、数据规约的技术和方法处理数据。培养快速学习和分享新知识，并在项目中使用的能力及独立解决问题的能力。

本次完成了：招聘网站的职位招聘数据的分位数图、分位数-分位数图以及散点图、使用线性回归算法拟合散点图处理。

后面我们研究：使用局部回归（Loess）曲线（增加一条光滑曲线到散布图）方法处理数据以及使用分箱、回归、聚类方法 检查离群点及光滑数据；