本文仅用于个人学习记录,使用的教材为汤家凤老师的《高等数学辅导讲义》。本文无任何盈利或者赚取个人声望的目的,如有侵权,请联系删除!
文章目录
- 一、中值定理
- 1.1 极值点
- 1.2 中值定理
- 1.2.1 罗尔中值定理
- 1.2.2 拉格朗日中值定理
- 1.2.3 柯西中值定理
- 1.2.4 泰勒中值定理
- 1.2.5 中值定理的几个推广形式
- 二、单调性与极值、凹凸性与拐点、函数作图
- 2.1 单调性与极值
- 2.1.1 单调性与极值的概念
- 2.1.2 单调性判别方法
- 2.1.3 极值点的判别步骤与方法
- 2.2 凹凸性与拐点
- 2.3 渐近线
- 2.4 弧微分、曲率与曲率半径
一、中值定理
1.1 极值点
极值点包括极大值点和极小值点。
设y = f(x)在x = a处取极值,则f’(a) = 0或f’(a)不存在,反之不对。
设f(x)可导且在x = a处取极值,则f’(a) = 0。
1.2 中值定理
1.2.1 罗尔中值定理
设f(x) ∈ C[a,b],在(a,b)内可导,f(a) = f(b),则存在ξ ∈ (a,b),使得f’(ξ) = 0。
1.2.2 拉格朗日中值定理
设f(x) ∈ C[a,b],在(a,b)内可导,则存在ξ ∈ (a,b),使得f’(ξ) = f ( b ) − f ( a ) b − a \frac{f(b) - f(a)}{b - a} b−af(b)−f(a)。
划重点
- 若题中出现f(b) - f(a),则一般使用拉格朗日中值定理。
- 若题中出现f(a),f( c),f(b),则一般使用两次拉格朗日中值定理。
- 已知关于f’(x)的结论,解关于f(x)的命题时,有时用拉格朗日中值定理。
1.2.3 柯西中值定理
设f(x),g(x) ∈ C[a,b],在(a,b)内可导,且g’(x) ≠ 0(a < x < b),则存在ξ ∈ (a,b),使得 f ( b ) − f ( a ) g ( b ) − g ( a ) \frac{f(b) - f(a)}{g(b) - g(a)} g(b)−g(a)f(b)−f(a) = f ′ ( ξ ) g ′ ( ξ ) \frac{f'(ξ)}{g'(ξ)} g′(ξ)f′(ξ)。
只要g’(x)在(a,b)内不等于0,即使g’(a) = 0或g’(b) = 0,柯西中值定理也成立。
1.2.4 泰勒中值定理
(泰勒中值定理1)如果函数f(x)在x0处具有n阶导数,那么存在x0的一个邻域,对于该邻域内的任意x,有f(x) = f(x0) + f’(x0)(x - x0) + f ′ ′ ( x 0 ) 2 ! \frac{f''(x_0)}{2!} 2!f′′(x0)(x - x0)2 + …… + f ( n ) ( x 0 ) n ! \frac{f\ ^{(n)}(x_0)}{n!} n!f (n)(x0)(x - x0)n + Rn(x)。其中Rn(x) = o((x - x0)n)称为佩亚诺型余项。
(泰勒中值定理2)如果函数f(x)在x0处具有n + 1阶导数,那么存在x0的一个邻域,对于该邻域内的任意x,有f(x) = f(x0) + f’(x0)(x - x0) + f ′ ′ ( x 0 ) 2 ! \frac{f''(x_0)}{2!} 2!f′′(x0)(x - x0)2 + …… + f ( n ) ( x 0 ) n ! \frac{f\ ^{(n)}(x_0)}{n!} n!f (n)(x0)(x - x0)n + Rn(x)。其中Rn(x) = o((x - x0)n+1)称为拉格朗日型余项。
当x0 = 0时,f(x) = f(x0) + f’(x0)(x - x0) + f ′ ′ ( x 0 ) 2 ! \frac{f''(x_0)}{2!} 2!f′′(x0)(x - x0)2 + …… + f ( n ) ( x 0 ) n ! \frac{f\ ^{(n)}(x_0)}{n!} n!f (n)(x0)(x - x0)n + Rn(x)称为f(x)的麦克劳林公式。常用的麦克劳林公式有

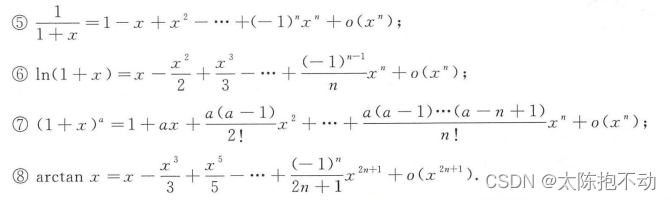
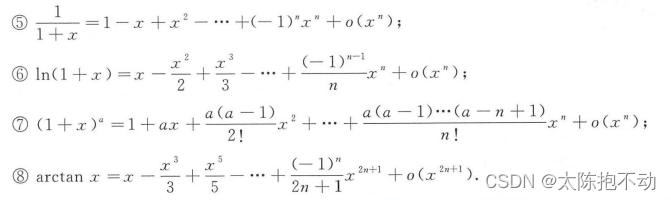
1.2.5 中值定理的几个推广形式
(导数零点定理)设f(x)在[a,b]上连续,在(a,b)内可导,且f+'(a)f-'(b) < 0,则存在ξ ∈ (a,b),使得f’(ξ) = 0。
(导数介值定理)设f(x)在[a,b]上连续,在(a,b)内可导,且f+'(a) ≠ f-'(b),不妨设f+'(a) < f-'(b),对任意的η ∈ (f+'(a),f-'(b)),存在ξ ∈ (a,b),使得f‘(ξ) = η。
二、单调性与极值、凹凸性与拐点、函数作图
2.1 单调性与极值
2.1.1 单调性与极值的概念
单调性的概念
设函数y = f(x)在D上有定义,若对任意的x1,x2 ∈ D
- x1 < x2,有f(x1) < f(x2),称f(x)在区域D上为严格的增函数。
- x1 < x2,有f(x1) > f(x2),称f(x)在区域D上为严格的减函数。
极值点的概念
- 函数f(x)在x = x0处左右去心邻域的函数值小于f(x0),称x = x0是f(x)的极大值点。
- 函数f(x)在x = x0处左右去心邻域的函数值大于f(x0),称x = x0是f(x)的极小值点。
2.1.2 单调性判别方法
- 若在区间I内有f’(x) > 0,则f(x)在I上严格增加。
- 若在区间I内有f’(x) < 0,则f(x)在I上严格减少。
划重点
- 以上定理反之不对。
- 若区间I内,除了有限个点外有f’(x) > 0,则f(x)在I上仍为严格增函数。
2.1.3 极值点的判别步骤与方法
极值点的判别步骤
- 确定函数的定义域x ∈ D
- 求f’(x),求出f(x)的驻点及不可导点(驻点就是导函数等于零的点)
- 判别法判别
极值点判别法
第一充分条件
- 左邻域内导数大于零,右邻域内导数小于零,为极大值点。
- 左邻域内导数小于零,右邻域内导数大于零,为极小值点。
第二充分条件
设函数f(x)在x = x0处二阶可导,且f’(x0) = 0,则
- 当f’'(x0) > 0时,x = x0为f(x)的极小值点。
- 当f’'(x0) < 0时,x = x0为f(x)的极大值点。
泰勒公式判别法
设f(x)具有n阶导数(n为偶数),且f(k)(x0) = 0(k = 1,2,3,……,n-1),则
- 当f(n)(x0) > 0时,x = x0为f(x)的极小值点。
- 当f(n)(x0) < 0时,x = x0为f(x)的极大值点。
2.2 凹凸性与拐点
凹凸性的概念
设y = f(x)定义在区间I上,若对任意的x1,x2 ∈ I,且x1 ≠ x2
- f( x 1 + x 2 2 \frac{x_1 + x_2}{2} 2x1+x2) > f ( x 1 ) + f ( x 2 ) 2 \frac{f(x_1) + f(x_2)}{2} 2f(x1)+f(x2),则称y = f(x)在I上为凸函数。
- f( x 1 + x 2 2 \frac{x_1 + x_2}{2} 2x1+x2) < f ( x 1 ) + f ( x 2 ) 2 \frac{f(x_1) + f(x_2)}{2} 2f(x1)+f(x2),则称y = f(x)在I上为凹函数。
拐点的概念
两侧凹凸性不同的点就叫做拐点。
曲线凹凸性的判别方法
方法一
- 若当x ∈ I时,f’'(x) > 0,则y = f(x)在I内为凹函数。
- 若当x ∈ I时,f’'(x) < 0,则y = f(x)在I内为凸函数。
方法二
设f(x)三阶可导,且f’‘(x) = 0,但f’‘’(x) ≠ 0,则(x0,f(x0))为曲线y = f(x)的拐点。
2.3 渐近线
| 名称 | 定义 |
|---|---|
| 水平渐近线 | 若 lim x → ∞ \lim_{x\rightarrow\infty} limx→∞f(x) = A,称y = A为曲线y = f(x)的水平渐近线(讨论正无穷负无穷) |
| 铅直渐近线 | 若 lim x → a \lim_{x\rightarrow\ a} limx→ af(x) = ∞ \infty ∞或f(a - 0) = ∞ \infty ∞或f(a + 0) = ∞ \infty ∞,称x = a为曲线y = f(x)的铅直渐近线 |
| 斜渐近线 | 若 lim x → ∞ \lim_{x\rightarrow\infty} limx→∞ f ( x ) x \frac{f(x)}{x} xf(x) = a(a ≠ 0, ∞ \infty ∞), lim x → ∞ \lim_{x\rightarrow\infty} limx→∞[f(x) - ax] = b,称y = ax + b为曲线y = f(x)的斜渐近线 |
若x = a为y = f(x)的铅直渐近线,则x = a为y = f(x)的间断点,反之不一定。
2.4 弧微分、曲率与曲率半径
弧微分
弧微分的基本公式(ds)2 = (dx)2 + (dy)2,其中

曲率与曲率半径
| 名称 | 计算公式 |
|---|---|
| 曲率 | k = ∣ y ′ ′ ∣ ( 1 + y ′ 2 ) 3 2 \frac{|y''|}{(1 + y'\ ^2)\ ^{\frac{3}{2}}} (1+y′ 2) 23∣y′′∣ |
| 曲率半径 | R = 1 k \frac{1}{k} k1 |