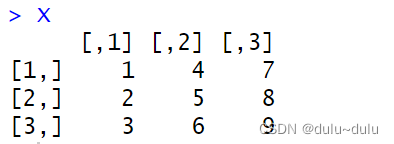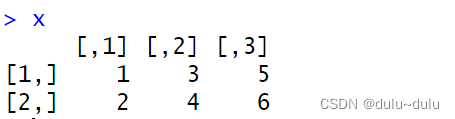R语言常用数组函数

news2024/11/23 7:25:40

目录

1.array

2.matrix

3.data.matrix

4.lower.tri

5.mat.or.vec 

6.t:转置矩阵

7.cbind

8.rbind

9.diag

10.aperm：对数组进行轴置换（维度重排）操作

11.%*%：乘法操作要求矩阵 A 的列数等于矩阵 B 的行数

12.crossprod:用于计算矩阵的交叉积

13.outer

14.Kronecker

15. apply

16.tapply

17.sweep:对矩阵的某个维度进行操作

18.aggregate

19.scale

20.matplot

21.cor

22.Contrast,row,col

1.array

array(data, dim = NULL, dimnames = NULL)
  • data：填充数组的数据向量或矩阵。
  • dim：指定数组的维度，即一个整数向量。例如，dim = c(3, 4, 2) 表示创建一个3行、4列、2个深度（即三维）的数组。
  • dimnames：指定数组维度的名称，通常是一个包含维度名称的列表。每个元素可以是字符向量，用于为相应维度的标签命名。

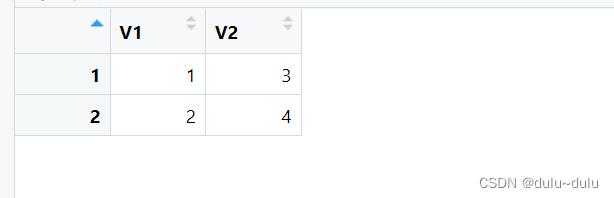
（1）创建一个二维数组

arr_2d <- array(data = c(1, 2, 3, 4), dim = c(2, 2))

 

 

（2）创建一个三维数组

arr_3d <- array(data = c(1, 2, 3, 4, 5, 6), dim = c(2, 3, 1))

 

 

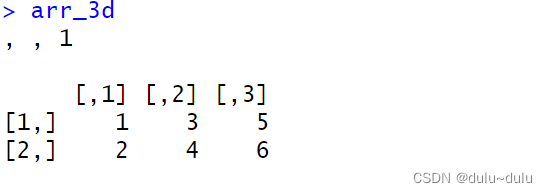
（3）创建一个具有维度名称的数组

arr_named <- array(data = c(1, 2, 3, 4), dim = c(2, 2), dimnames = list(c("row1", "row2"), c("col1", "col2")))

 

2.matrix

matrix(data, nrow = 1, ncol = 1, byrow = FALSE, dimnames = NULL)
  • data：用于填充矩阵的数据向量或矩阵。
  • nrow：指定矩阵的行数。
  • ncol：指定矩阵的列数。
  • byrow：逻辑值，指定是否按行填充矩阵，默认为FALSE表示按列填充。
  • dimnames：矩阵维度的名称。
# 创建一个2行3列的矩阵
mat <- matrix(data = c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3)

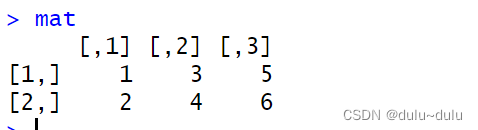
3.data.matrix

# 创建一个数据框
df <- data.frame(a = c(1, 2, 3),
                 b = c(4, 5, 6),
                 c = c(7, 8, 9))

# 将数据框转换为数值型矩阵
mat <- data.matrix(df)

# 打印输出结果
print(mat)

 

4.lower.tri

# 创建一个3x3的矩阵
mat <- matrix(c(1, 2, 3, 4, 5, 6, 7, 8, 9), nrow = 3)

# 提取矩阵的下三角部分
lower_tri <- lower.tri(mat)

# 打印输出结果
print(lower_tri)

 

5.mat.or.vec

# 生成一个2行3列的零矩阵
m <- mat.or.vec(nr = 2, nc = 3)

# 生成一个含有5个元素的零向量
v <- mat.or.vec(nr = 5, nc = 1)

 

6.t:转置矩阵

# 创建一个3x2的矩阵
mat <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 3)

# 对矩阵进行转置
transposed_mat <- t(mat)

# 打印输出结果
print(transposed_mat)

 

7.cbind

# 创建两个向量
v1 <- c(1, 2, 3)
v2 <- c(4, 5, 6)

# 将两个向量按列合并
result <- cbind(v1, v2)

# 打印输出结果
print(result)

 

8.rbind

# 创建两个向量
v1 <- c(1, 2, 3)
v2 <- c(4, 5, 6)

# 将两个向量按行合并
result <- rbind(v1, v2)

# 打印输出结果
print(result)

 

9.diag

获取对角矩阵元素

# 创建一个3x3的矩阵
mat <- matrix(c(1, 2, 3, 4, 5, 6, 7, 8, 9), nrow = 3)

# 获取矩阵的对角元素向量
diag_vec <- diag(mat)

# 打印输出结果
print(diag_vec)

#输出 [1] 1 5 9

生成对角矩阵

# 创建一个5x5的对角矩阵，对角线上的元素为1
diag_mat <- diag(1, nrow = 5)

# 打印输出结果
print(diag_mat)

 

10.aperm：对数组进行轴置换（维度重排）操作

# 创建一个3x4x2的三维数组
arr <- array(1:24, dim = c(3, 4, 2))第一个维度行数，第二个维度列数，第三个维度层数

# 对数组进行轴置换，重新排列维度
permuted_arr <- aperm(arr, perm = c(3, 2, 1))
#将第一个元素排在最后，第二个元素排在中间，第三个元素排在第一个，即(2,4,3)

# 打印输出结果
print(permuted_arr)

 

11.%*%：乘法操作要求矩阵 A 的列数等于矩阵 B 的行数

# 创建两个矩阵
A <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)
B <- matrix(c(5, 6, 7, 8), nrow = 2, ncol = 2)

# 执行矩阵乘法
C <- A %*% B

# 打印结果
print(C)

矩阵A

     [,1] [,2]
[1,]    1    3
[2,]    2    4
矩阵B

     [,1] [,2]
[1,]    5    7
[2,]    6    8

 矩阵乘法运算

c_11 = (1*5) + (3*6) = 5 + 18 = 23#A的第一行，B的第一列

c_12 = (1*7) + (3*8) = 7 + 24 = 31#A的第一行，B的第二列

c_21 = (2*5) + (4*6) = 10 + 24 = 34#A的第二行，B的第一列

c_22 = (2*7) + (4*8) = 14 + 32 = 46#A的第二行，B的第二列

矩阵C的值

      [,1] [,2]
[1,]   23   31
[2,]   34   46

 

12.crossprod:用于计算矩阵的交叉积

# 创建向量
x <- c(1, 2, 3)
y <- c(4, 5, 6)

# 计算向量的内积
result <- crossprod(x, y)

# 打印结果
print(result)

     [,1]
[1,]   32

计算过程：

 [1, 2, 3] * [4, 5, 6] = (1 * 4) + (2 * 5) + (3 * 6) = 4 + 10 + 18 = 32

# 创建矩阵
A <- matrix(c(1, 2, 3, 4), nrow = 2, ncol = 2)

# 计算矩阵的交叉积
result <- crossprod(A)

# 打印结果
print(result)

矩阵A

     [,1] [,2]
[1,]    1    3
[2,]    2    4
转置后的矩阵A

     [,1] [,2]
[1,]    1    2
[2,]    3    4

     [,1] [,2]
[1,]    1*1 + 2*2   1*3 + 2*4
[2,]    3*1 + 4*2   3*3 + 4*4
 

    [,1] [,2]
[1,]    5   11
[2,]   11   25

 

13.outer

# 创建向量
x <- c(1, 2, 3)

# 计算向量元素之间的外积
result <- outer(x, x)

# 打印结果
print(result)

#矩阵中的第 i 行和第 j 列的元素是向量 x 中的第 i 个元素与第 j 个元素的乘积。

     [,1] [,2] [,3]
[1,]   1*1    1*2    1*3
[2,]    2*1    2*2    2*3
[3,]    3*1    3*2    3*3

 

14.Kronecker

# 创建两个矩阵
A <- matrix(c(1, 2, 3, 4), nrow = 2)
B <- matrix(c(5, 6, 7, 8), nrow = 2)

# 计算Kronecker积
result <- kronecker(A, B)

# 打印结果
print(result)

 

     [,1] [,2] [,3] [,4]
[1,]    1*5   1*6   2*5   2*6#第一列*第一列
[2,]    1*7   1*8   2*7   2*8#第一列*第二列
[3,]   3*5   3*6   4*5    4*6#第二列*第一列
[4,]   3*7   3*8   4*7    4*8#第二列*第二列
 

15. apply

apply(X, MARGIN, FUN)

X 是要操作的矩阵或数组

MARGIN 指定要应用函数的维度（1表示行，2表示列，其他值表示整个维度）

FUN 是要应用的函数。

# 创建一个矩阵
X <- matrix(1:9, nrow = 3)

# 对每一行求和
row_sums <- apply(X, 1, sum)
print(row_sums)

# 对每一列取平均值
col_means <- apply(X, 2, mean)
print(col_means)

# 对整个矩阵进行乘法运算
matrix_product <- apply(X, c(1, 2), function(x) x * 2)
print(matrix_product)

 [1]  6 15 24
[1] 2 5 8


     [,1] [,2] [,3]
[1,]    2    8   18
[2,]    4   10   20
[3,]    6   12   22

 

16.tapply

tapply(X, INDEX, FUN)

X 是要操作的向量或矩阵

INDEX 是一个或多个因子，用于指定分组依据

FUN 是要应用的函数。

# 创建一个向量
x <- c(1, 2, 3, 4, 5, 6)

# 定义一个因子，用于分组
group <- c("A", "B", "A", "B", "A", "B")

# 对向量按照因子进行分组，并对每个组求和
result <- tapply(x, group, sum)
print(result)

  A  B 
  9 12 

17.sweep:对矩阵的某个维度进行操作

sweep(x, MARGIN, STATS, FUN = "-", ...)

 x是要进行操作的矩阵

MARGIN指定要操作的维度（1为行，2为列）

STATS是要进行操作的向量或矩阵；FUN是要应用的函数，它将用于在矩阵的指定维度上进行操作，默认为减法（-）。

# 创建一个矩阵
x <- matrix(1:6, nrow = 2)

# 创建一个要进行操作的向量
stats <- c(3, 2)

# 对矩阵的每一列进行减法操作
result <- sweep(x, 2, stats, FUN = "-")
print(result)

 每个元素-2

     [,1] [,2]
[1,]   -2   -1
[2,]   -1    0

 

18.aggregate

aggregate(formula, data, FUN, ...)

formula 是一个公式，指定了要汇总的变量和分组因子

data 是包含要汇总的数据的数据框

FUN 是要应用的函数

  • sum(): 求和
  • mean(): 平均值
  • median(): 中位数
  • min(): 最小值
  • max(): 最大值
  • length(): 长度（计数）
# 创建一个数据框
df <- data.frame(
  group = c("A", "A", "B", "B", "A", "B"),
  value = c(1, 2, 3, 4, 5, 6)
)

# 对数据框按照 group 列进行分组，并对每个组计算平均值
result <- aggregate(value ~ group, data = df, FUN = mean)
print(result)

  group value
1     A   2.666667
2     B   4.333333

19.scale

scaled_data <- scale(x, center = TRUE, scale = TRUE)

x 是要进行标准化处理的向量、矩阵或数据框；

center 参数用于指定是否进行中心化，默认为 TRUE，表示进行中心化；

scale 参数用于指定是否进行缩放，默认为 TRUE，表示进行缩放。

# 创建一个矩阵
x <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 3)

# 对矩阵按列进行标准化处理
scaled_data <- scale(x, center = TRUE, scale = TRUE)
print(scaled_data)

#通过标准化处理，每列的均值被转换成了 0，标准差变成了 1

#第一列的标准化结果是 [-1.2247449, 0.0000000, 1.2247449]

#第二列的标准化结果也是 [-1.2247449, 0.0000000, 1.2247449]。

           [,1]       [,2]
[1,] -1.2247449 -1.2247449
[2,]  0.0000000  0.0000000
[3,]  1.2247449  1.2247449

 

20.matplot

matplot(x, y = NULL, type = "l", lty = 1, lwd = 1, col = 1, pch = NULL, ...)

x 是一个矩阵或数据框，它的每列（或每行）代表一个变量；

y 是一个可选参数，当 x 为单个矩阵时，y 可以为 NULL，当 x 为两个矩阵时，y 表示第二个矩阵；

type 参数指定绘图类型，可以是 "l"（线图）或 "p"（点图）；

lty、lwd、col 和 pch 分别指定线型、线宽、颜色和点的形状等。

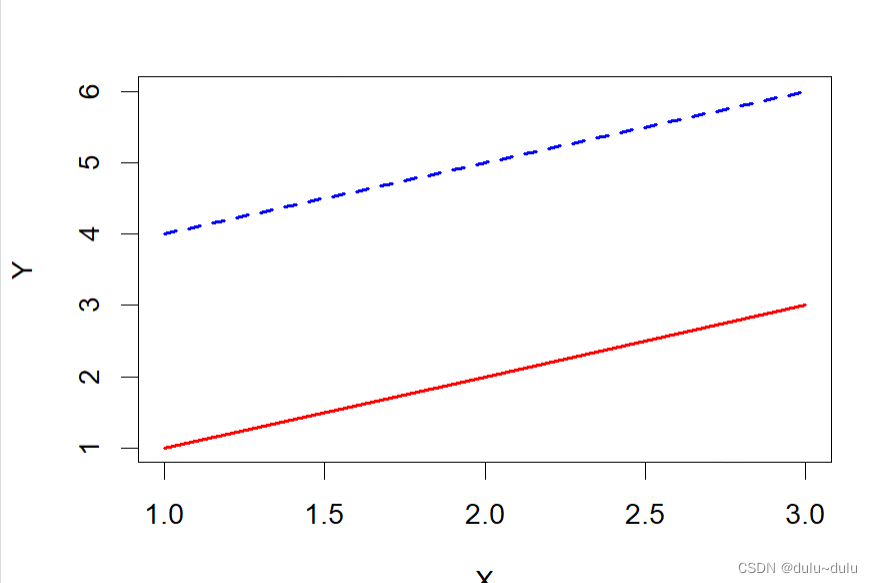
# 创建一个矩阵
x <- matrix(c(1, 2, 3, 4, 5, 6), nrow = 3)

# 使用 matplot() 绘制线图
matplot(x, type = "l", lwd = 2, col = c("red", "blue"), xlab = "X", ylab = "Y")

 

21.cor

cor(x, y = NULL, use = "everything", method = c("pearson", "kendall", "spearman"))

x 和 y 是要计算相关系数的向量、矩阵或数据框；

use 参数用于指定处理缺失值的方式，默认为 "everything"，表示包括所有的缺失值；method 参数用于指定使用的相关系数类型，默认为 "pearson"，还可以是 "kendall"（肯德尔相关系数）或 "spearman"（斯皮尔曼相关系数）。

# 创建两个向量
x <- c(1, 2, 3, 4, 5)
y <- c(2, 4, 6, 8, 10)

# 使用 cor() 计算两个向量的相关系数
correlation <- cor(x, y)
print(correlation)

[1] 1

向量 x 和 y 是完全正相关的，相关系数为 1。

22.Contrast,row,col

#假设有一个包含销售数据的矩阵，其中行表示不同的产品，列表示不同的地区。

Contrast：对照矩阵:其每一行代表一种对照或比较，每一列表示一种变量或影响因素。对照矩阵描述了不同对照之间的差异

row：矩阵的行下标集：可以使用行下标集来选择该产品所在的行

col：求列下标集 :使用列下标集来选择这几个地区所在的列。

整理不易，若有遗漏或错误，请大佬们不吝赐教！！❤❤❤ 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/942355.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基于梯度算法优化的BP神经网络（预测应用） - 附代码

基于梯度算法优化的BP神经网络（预测应用） - 附代码

基于梯度算法优化的BP神经网络&#xff08;预测应用&#xff09; - 附代码 文章目录 基于梯度算法优化的BP神经网络&#xff08;预测应用&#xff09; - 附代码1.数据介绍2.梯度优化BP神经网络2.1 BP神经网络参数设置2.2 梯度算法应用 4.测试结果&#xff1a;5.Matlab代码 摘要…
阅读更多...
计算机组成原理之数据的表示和运算（一）

计算机组成原理之数据的表示和运算（一）

目录 一、引言二、进位计数制2.1 十进制计数法2.2 二进制2.3 八进制2.4 十六进制2.5 进制转换&#xff1a;二进制、八进制、十六进制、十进制之间的转换2.5.1 任意进制到十进制转换2.5.2 二进制与八进制和十六进制如何进行互相转换&#xff1f;2.5.3 十进制到任意进制的转换 2.…
阅读更多...
layui框架学习（42：文件上传模块-上）

layui框架学习（42：文件上传模块-上）

之前学习asp.net core编程入门教程时结合layui测试过文件上传《基于ASP.Net Core和Layui的多文件上传》&#xff0c;但没有认真学习过layui的文件上传模块&#xff0c;本文开始&#xff0c;计划分两章学习并记录文件上传模块中的属性、事件及函数的使用方法。   layui中的文件…
阅读更多...
1.1 数据库系统简介

1.1 数据库系统简介

1.1.数据库系统简介 前言&#xff1a; 数据库系统是一个软件系统&#xff0c;用于管理和操作数据库。它提供了一个组织良好、高效并能够方便存取的数据存储机制&#xff0c;并且能够支持各种数据操作、事务管理、并发控制和恢复功能。以下是数据库系统的一些主要特点和组件&a…
阅读更多...
redis缓存雪崩、穿透、击穿解决方案

redis缓存雪崩、穿透、击穿解决方案

redis缓存雪崩、穿透、击穿解决方案 背景缓存雪崩缓存击穿缓存穿透总结背景 关于缓存异常，我们常见的有三个问题：缓存雪崩、缓存击穿、缓存穿透。这三个问题一旦发生，会导致大量请求直接落到数据库层面。如果请求的并发量很大，会影响数据库的运行，严重的会导致数据库宕机…
阅读更多...
xsschallenge1~13通关详细教程

xsschallenge1~13通关详细教程

文章目录 XSS 挑战靶场通关level1level2level3level4level5level6level7level8level9level10level11level12level13 XSS 挑战靶场通关 level1 通过观察发现这个用户信息可以修改 那么我们直接输入攻击代码 <script>alert(/wuhu/)</script>弹框如下&#xff1a; …
阅读更多...
烟花厂人员作业释放静电行为检测算法

烟花厂人员作业释放静电行为检测算法

烟花厂人员作业释放静电行为检测算法通过pythonyolo系列算法模型框架&#xff0c;烟花厂人员作业释放静电行为检测算法在工厂车间入口处能够及时捕捉到人员是否触摸静电释放仪。一旦检测到人员进入时没有触摸静电释放仪&#xff0c;系统将自动触发告警。Python是一种由Guido va…
阅读更多...
第 1 章 绪论（计算多项式）

第 1 章 绪论（计算多项式）

示例代码 1&#xff1a; /* 计算 1 - 1 / x 1 / x * x - ... */#include <stdio.h> #include <sys/timeb.h>int main(void) {double x;int n;printf("Please input x and n: ");scanf_s("%lf%d", &x, &n);struct timeb t1;ftime(&…
阅读更多...
2023.8.27 关于 Junit5 详解

2023.8.27 关于 Junit5 详解

目录 引言 注解 断言 用例的执行顺序 参数化 测试套件 引言 Junit 是一个基于Java语言的单元测试框架Selenium 是一个用于Web应用程序测试的自动化测试框架结合二者能让我们的 Web自动化测试 更加完善和全面 注意&#xff1a; 本文所讲的内容&#xff0c;均基于以下依…
阅读更多...
机器视觉工程师永不为奴，他们是肯干肯出差肯加班肯拼命肯被使唤肯被叼

机器视觉工程师永不为奴，他们是肯干肯出差肯加班肯拼命肯被使唤肯被叼

​ 永不为奴&#xff0c;为什么这样呐喊&#xff0c;真的很难做到。我们职业机器视觉工程师&#xff0c;本身职业具有一大特点就是专业性。 但是我们机器视觉工程师是专业技术绝不苟同于不是技术人员言语&#xff0c;我们很专业。 肯出差&#xff1a; 设备去那里&#xff0c;…
阅读更多...
启莱OA CloseMsg.aspx SQL注入

启莱OA CloseMsg.aspx SQL注入

子贡曰&#xff1a;“贫而无谄&#xff0c;富而无骄&#xff0c;何如&#xff1f;”子曰&#xff1a;“可也。未若贫而乐&#xff0c;富而好礼者也。” 子贡曰&#xff1a;“《诗》云&#xff1a;‘如切如磋&#xff0c;如琢如磨。’其斯之谓与&#xff1f;”子曰&#xff1a;“…
阅读更多...
mybatis plus新版代码生成器，类型转换处理器ITypeConvertHandler使用

mybatis plus新版代码生成器，类型转换处理器ITypeConvertHandler使用

目录 引言关键代码源码分析记录一坑类型转换的第二种方式完整源码地址 引言 当默认生成的数据类型不满足时&#xff0c;就需要自定义指定要生成的类型 关键代码 FastAutoGenerator.create(url, username, password).dataSourceConfig(builder -> {builder.typeConvertHandl…
阅读更多...
Python计算加速利器

Python计算加速利器

迷途小书童的 Note 读完需要 6分钟 速读仅需 2 分钟 1 简介 Python 是一门应用非常广泛的高级语言&#xff0c;但是&#xff0c;长久以来&#xff0c;Python的运行速度一直被人诟病&#xff0c;相比 c/c、java、c#、javascript 等一众高级编程语言&#xff0c;完全没有优势。 那…
阅读更多...
记一次因函数入参没有带类型所引发的问题

记一次因函数入参没有带类型所引发的问题

工作中&#xff0c;sit测试中&#xff0c;测试突然发现页面异常。经排查&#xff0c;是函数参数没有定义类型所以&#xff0c;dart默认是dynamic类型&#xff0c;而dynamic编译阶段不检查类型&#xff0c;正是由于编译阶段不检查类型&#xff0c;很明显的错误也只能运行的时候才…
阅读更多...
【Axure高保真原型】中继器网格图片拖动摆放

【Axure高保真原型】中继器网格图片拖动摆放

今天和大家分享中继器网格图片拖动摆放的原型模板&#xff0c;我们可以通过鼠标拖动来移动图片&#xff0c;拖动过程其他图标会根据图片拖动自动排列&#xff0c;松开鼠标是图片停放在指定位置&#xff0c;其他图标自动排列。那这个模板是用中继器制作的&#xff0c;所以使用也…
阅读更多...
C# 跨线程访问窗体控件

C# 跨线程访问窗体控件

在不加任何修饰的情况下&#xff0c;C# 默认不允许跨线程访问控件&#xff0c;实际在项目开发过程中&#xff0c;经常使用跨线程操作控件属性&#xff0c;需要设置相关属性才能正确使用&#xff0c;两种方法设置如下&#xff1a; 方法1&#xff1a;告诉编译器取消跨线程访问检…
阅读更多...
XML—标记语言

XML—标记语言

什么是XML&#xff1f; Extensible Markup Language&#xff0c;可扩展标记语言。 那标记语言是什么&#xff1f; 用文字做标记表达一些效果或携带一些数据。比如&#xff1a;HTML、XML 我的理解&#xff1a;用倾盆大雨表达雨很大 那XML为什么说是可扩展的呢&#xff1f; 还…
阅读更多...
ethers.js9、过滤事件

ethers.js9、过滤事件

在 合约监听 的基础上，我们拓展一下，在监听的过程中增加过滤器，监听指定地址的转入转出。 过滤器 当合约创建日志（释放事件）时，它最多可以包含[4]条数据作为索引（indexed）。索引数据经过哈希处理并包含在布隆过滤器中，这是一种允许有效过滤的数据结构。因此，一个事件…
阅读更多...
Java学数据结构（4）——散列表Hash table 散列函数 哈希冲突

Java学数据结构（4）——散列表Hash table 散列函数 哈希冲突

目录 引出散列表Hash table关键字Key和散列函数(hash function)散列函数解决collision哈希冲突&#xff08;碰撞&#xff09;分离链接法(separate chaining)探测散列表(probing hash table)双散列(double hashing) Java标准库中的散列表总结 引出 1.散列表&#xff0c;key&…
阅读更多...
SQLite数据库C_C++接口（保姆级API应用 1.4W字）（全网最详细介绍，学完必掌握）

SQLite数据库C_C++接口（保姆级API应用 1.4W字）（全网最详细介绍，学完必掌握）

目录 sqlite3的C/C API应用 前言 SQLite3库安装 API函数 打开、关闭、错误处理 打开 返回值 关闭 错误调试 实际应用 执行SQL&#xff08;DDL、DML&#xff09; API介绍 实际应用 回调函数查询 API介绍 实际应用 全缓冲查询 API介绍 实际应用 字节缓冲查询…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023