在正式的学习 C 语言之前，我们需要先了解计算机组成原理相关的知识。

一、引言

现代计算机的结构如下图所示：

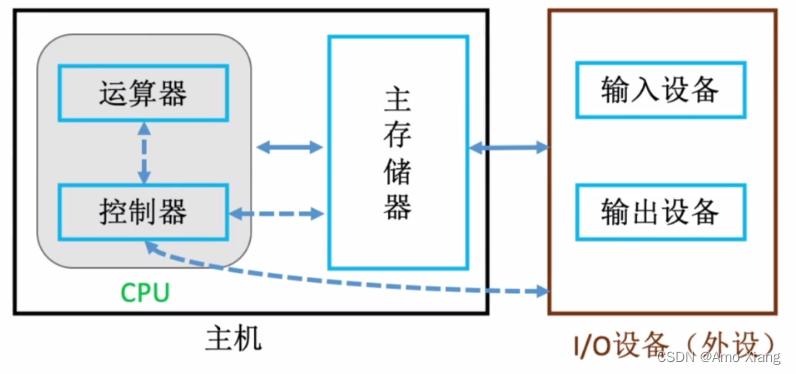
数据如何在计算机中表示？运算器如何实现数据的算术、逻辑运算？

二、进位计数制

本小节内容大致如下：

最古老的计数方法：

2.1 十进制计数法

补充说明：

我们平时使用的数字都是由 0~9 共十个数字组成的，例如 1、6、10、297、952 等，一个数字最多能表示九，如果要表示十、十一、二十九、一百等，就需要多个数字组合起来。例如表示 5+8 的结果，一个数字不够，只能 进位，用 13 来表示；这时 进一位 相当于十，进两位 相当于二十。因为逢十进一（满十进一），也因为只有 0~9 共十个数字，所以叫做 十进制(Decimalism)。 十进制是在人类社会发展过程中自然形成的，它符合人们的思维习惯，例如人类有十根手指，也有十根脚趾。进制也就是进位制。进行加法运算时 逢X进一(满X进一)，进行减法运算时 借一当X，这就是X进制，这种进制也就包含X个数字，基数为X。十进制有 0~9 共10个数字，基数为10，在加减法运算中，逢十进一，借一当十。

推广：r进制计数法，如下图所示：

2.2 二进制

我们不妨将思维拓展一下，既然可以用 0~9 共十个数字来表示数值，那么也可以用 0,1 两个数字来表示数值，这就是 二进制(Binary)。 例如，数字 0,1,10,111,100,1000001 都是有效的二进制。在计算机系统内部，所有的信息都是用二进制进行编码的，这样做的原因有以下几点：

① 二进制只有两种状态，使用有两个稳定状态的物理器件就可以表示二进制的每一位，制造成本比较低，例如用高低电平或电荷的正负极性都可以很方便地表示 0和1
② 二进制位 1和0 正好与逻辑值 真和假 对应，为计算机实现逻辑运算和程序中的逻辑判断提供了便利条件。
③ 二进制的编码和运算规则都很简单，通过逻辑门电路能方便地实现算术运算。二进制是学习编程必须掌握的基础

二进制加减法和十进制加减法的思想是类似的：

对于十进制，进行加法运算时逢十进一，进行减法运算时借一当十
对于二进制，进行加法运算时逢二进一，进行减法运算时借一当二

下面两张示意图详细演示了二进制加减法的运算过程。二进制加法：

1+0=1、1+1=10、11+10=101、111+111=1110

演示如下图所示：

二进制减法：

1-0=1、10-1=1、101-11=10、1100-111=101

演示如下图所示：

2.3 八进制

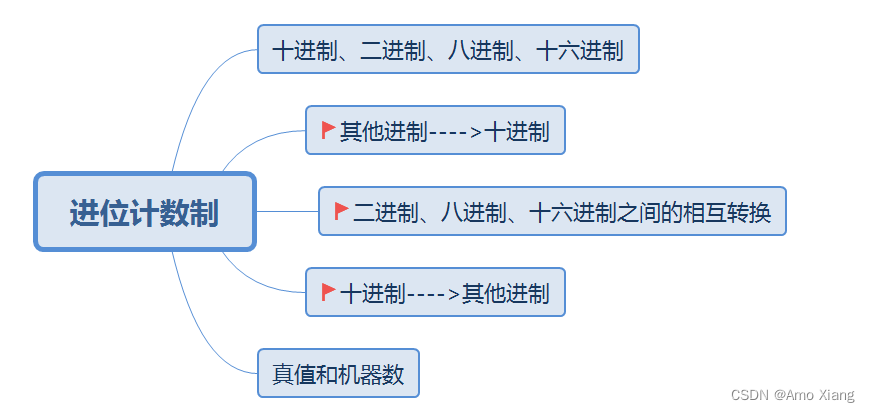
八进制有 0~7 共 8个 数字，基数为8，加法运算时 逢八进一，减法运算时 借一当八。例如，数字 0,1,5,7,14,733,67001,25430 都是有效的八进制。八进制加法：

3+4=7、5+6=13、75+42=137、2427+567=3216

演示如下图所示：

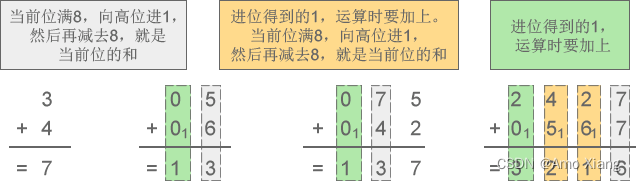
八进制减法：

6-4=2、52-27=23、307-141=146、7430-1451=5757

演示如下图所示：

2.4 十六进制

除了二进制和八进制，十六进制也经常使用，甚至比八进制还要频繁。十六进制中，用 A 来表示 10，B 表示 11，C 表示 12，D 表示 13，E 表示 14，F 表示 15，因此有 0~F 共 16 个数字，基数为 16，加法运算时 逢16进1，减法运算时 借1当16。例如，数字 0,1,6,9,A,D,F,419,EA32,80A3,BC00 都是有效的十六进制。

注意，十六进制中的字母不区分大小写，ABCDEF 也可以写作 abcdef。

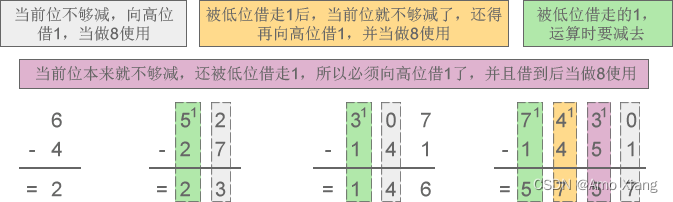
十六进制加法：

6+7=D、18+BA=D2、595+792=D27、2F87+F8A=3F11

演示如下图所示：

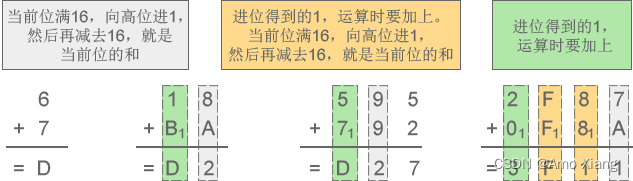
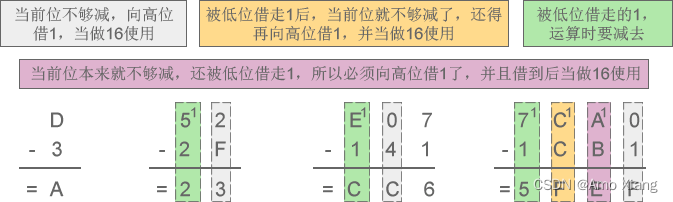
十六进制减法：

D-3=A、52-2F=23、E07-141=CC6、7CA0-1CB1=5FEF

演示如下图所示：

2.5 进制转换：二进制、八进制、十六进制、十进制之间的转换

2.5.1 任意进制到十进制转换

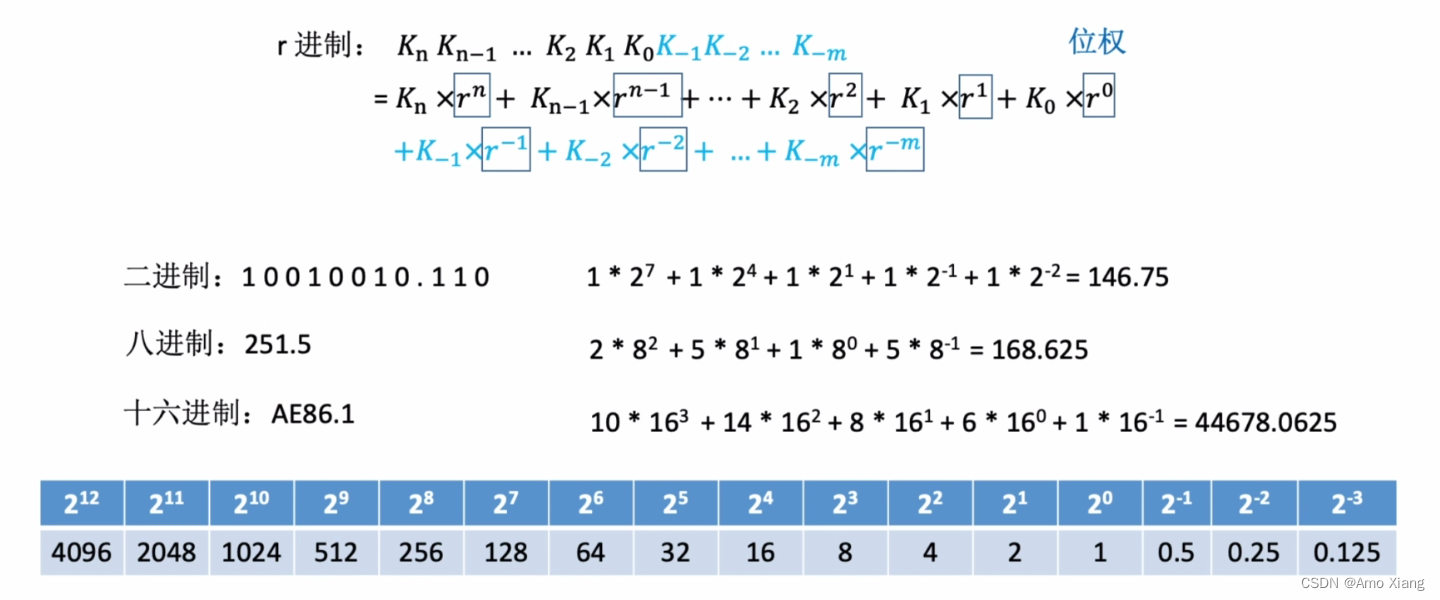
更多转换成十进制的例子：

二进制：1001 = 1×2³ + 0×2² + 0×2¹+ 1×2⁰ = 8 + 0 + 0 + 1 = 9（十进制）
二进制：101.1001 = 1×2² + 0×2¹ + 1×2⁰ + 1×2^-1 + 0×2^-2 + 0×2^-3 + 1×2^-4 = 4 + 0 + 1 + 0.5 + 0 + 0 + 0.0625 = 5.5625（十进制）
八进制：302 = 3×8² + 0×8¹ + 2×8⁰ = 192 + 0 + 2 = 194（十进制）
八进制：302.46 = 3×8² + 0×8¹ + 2×8⁰ + 4×8^-1 + 6×8^-2 = 192 + 0 + 2 + 0.5 + 0.09375= 194.59375（十进制）
十六进制：EA7 = 14×16² + 10×16¹ + 7×16⁰ = 3751（十进制）

2.5.2 二进制与八进制和十六进制如何进行互相转换？

**各种进制常见的书写方式：**

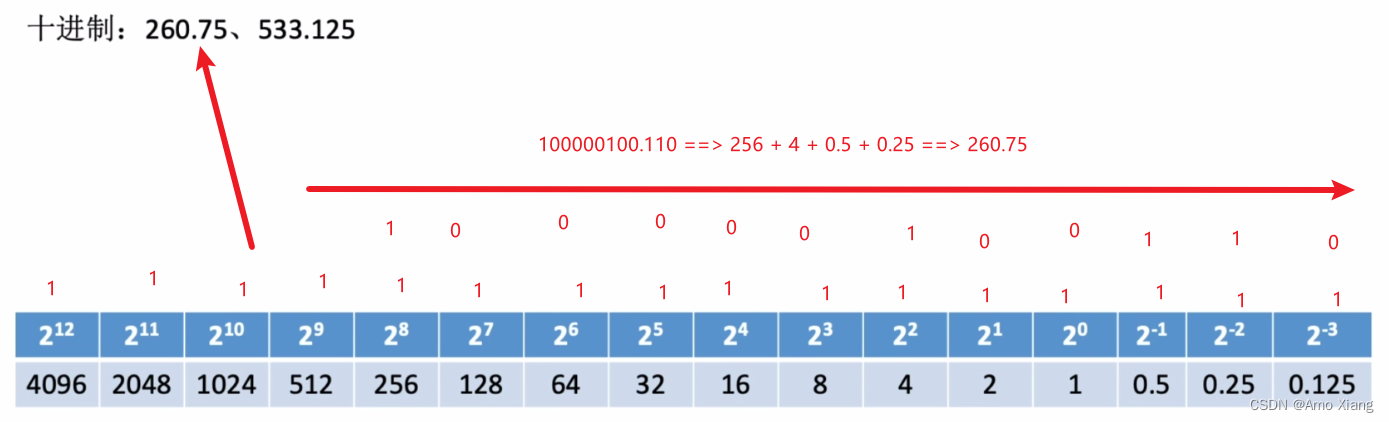
2.5.3 十进制到任意进制的转换

整数部分：

小数部分：

十进制到二进制拼凑法：

2.6 真值和机器数

2.7 小结

中国古代的二进制系统：

三、BCD 码

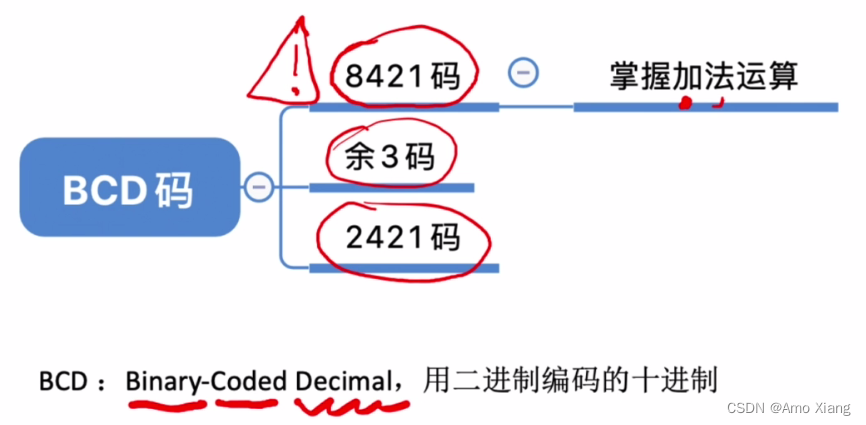
8421 码操作如下：

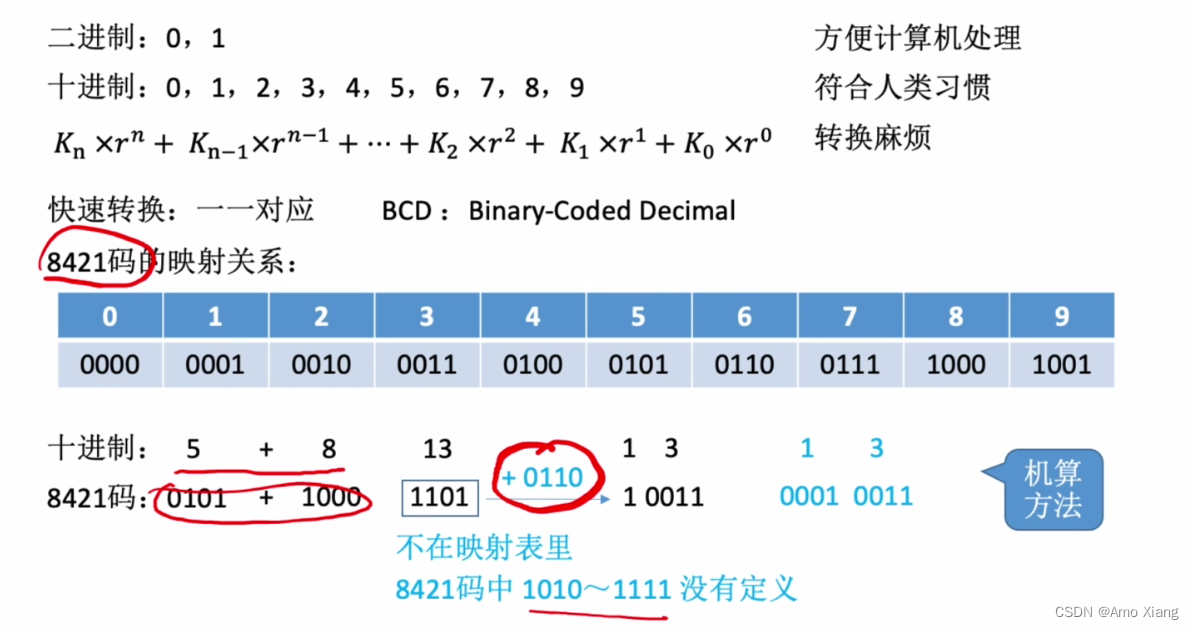
注： 若相加结果在合法范围内，则无需修正。 其余码：

小结：

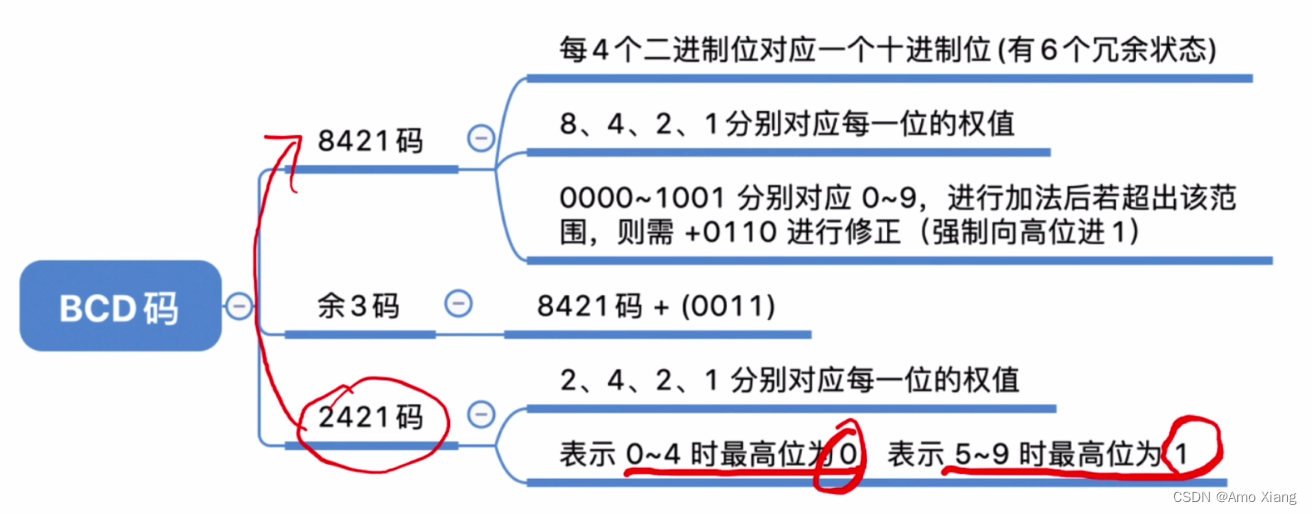
四、无符号整数的表示和运算

4.1 无符号整数在计算机中的应用

4.2 无符号整数的表示

实例：

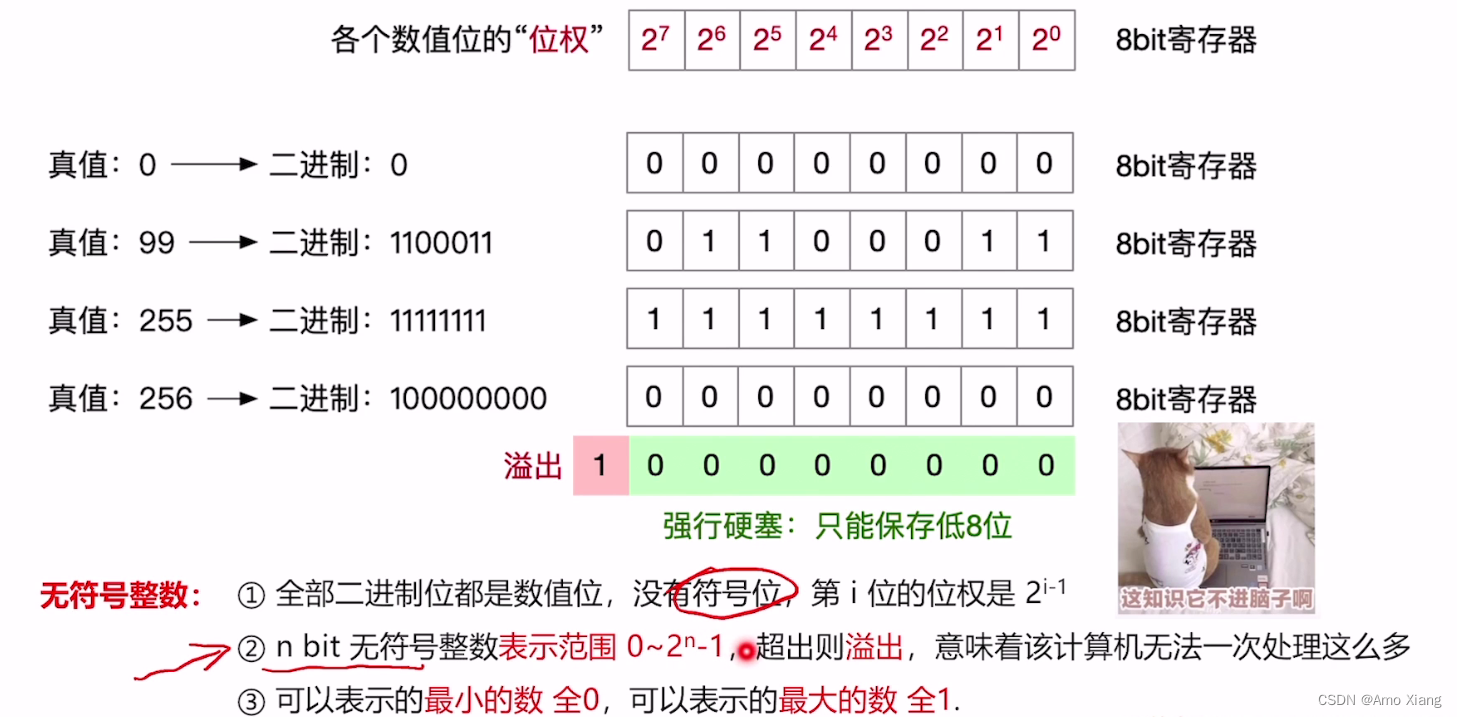
4.3 无符号整数的加法运算

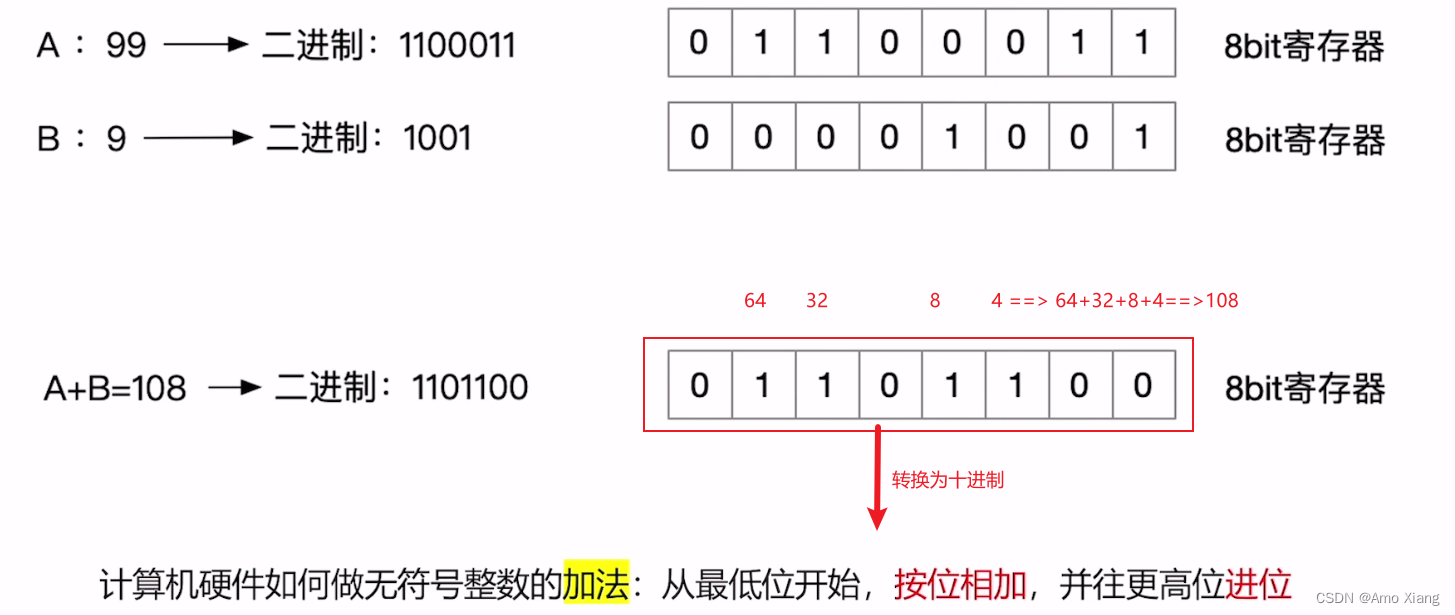
4.4 无符号整数的减法运算

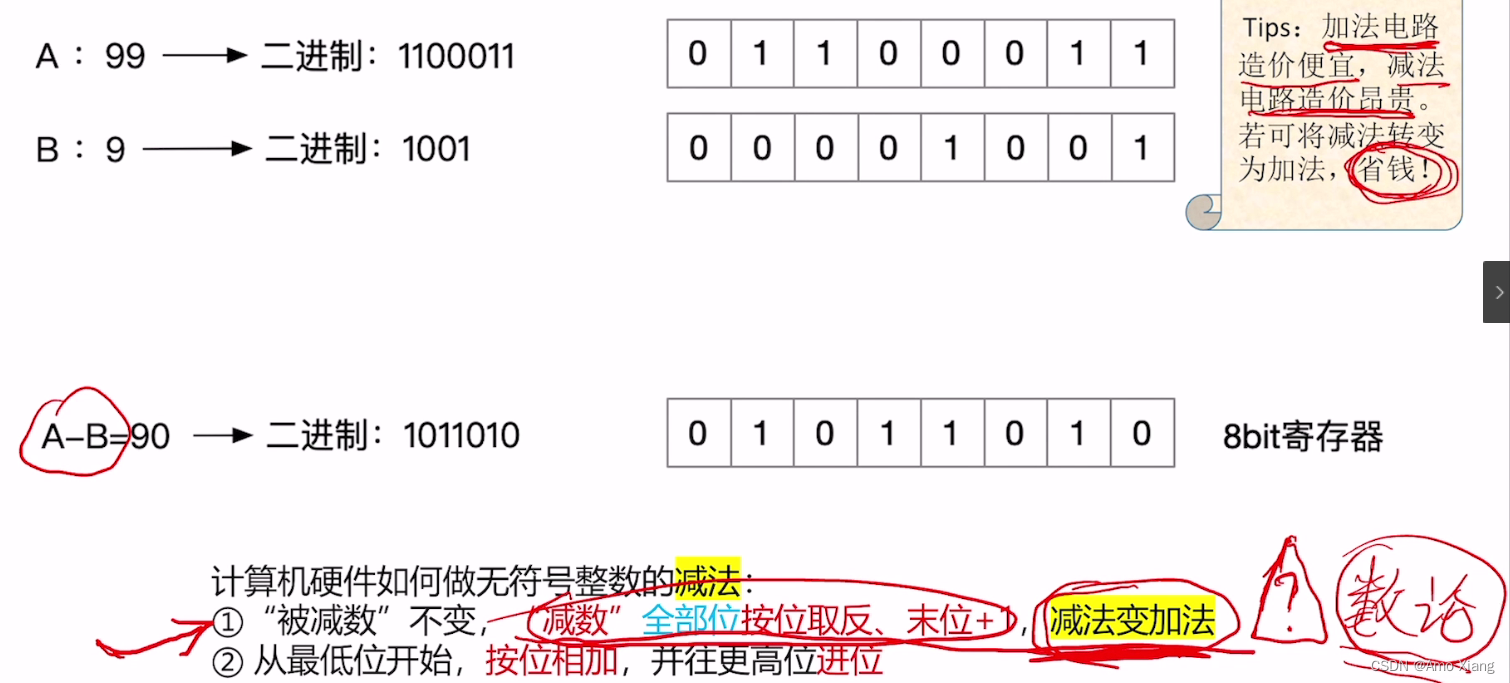
具体实现过程：① 全部位按位取反，末位+1

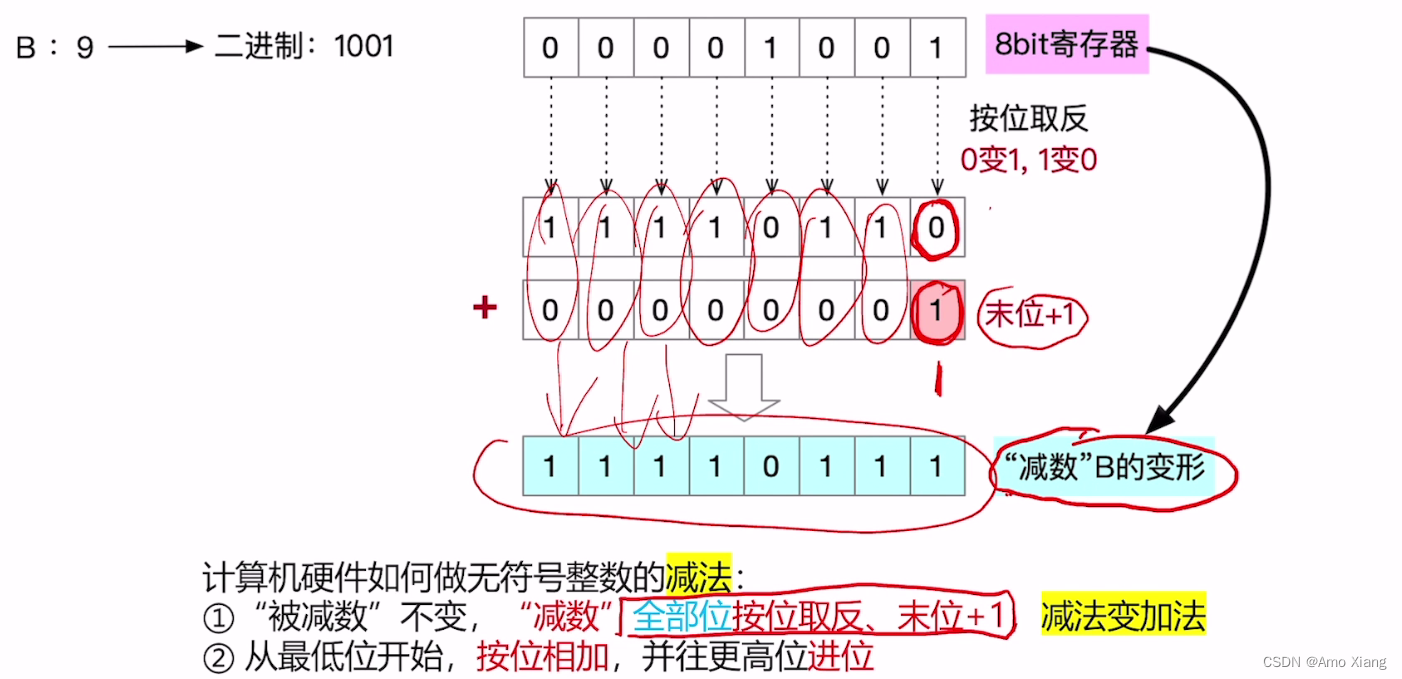
② 减法变加法：

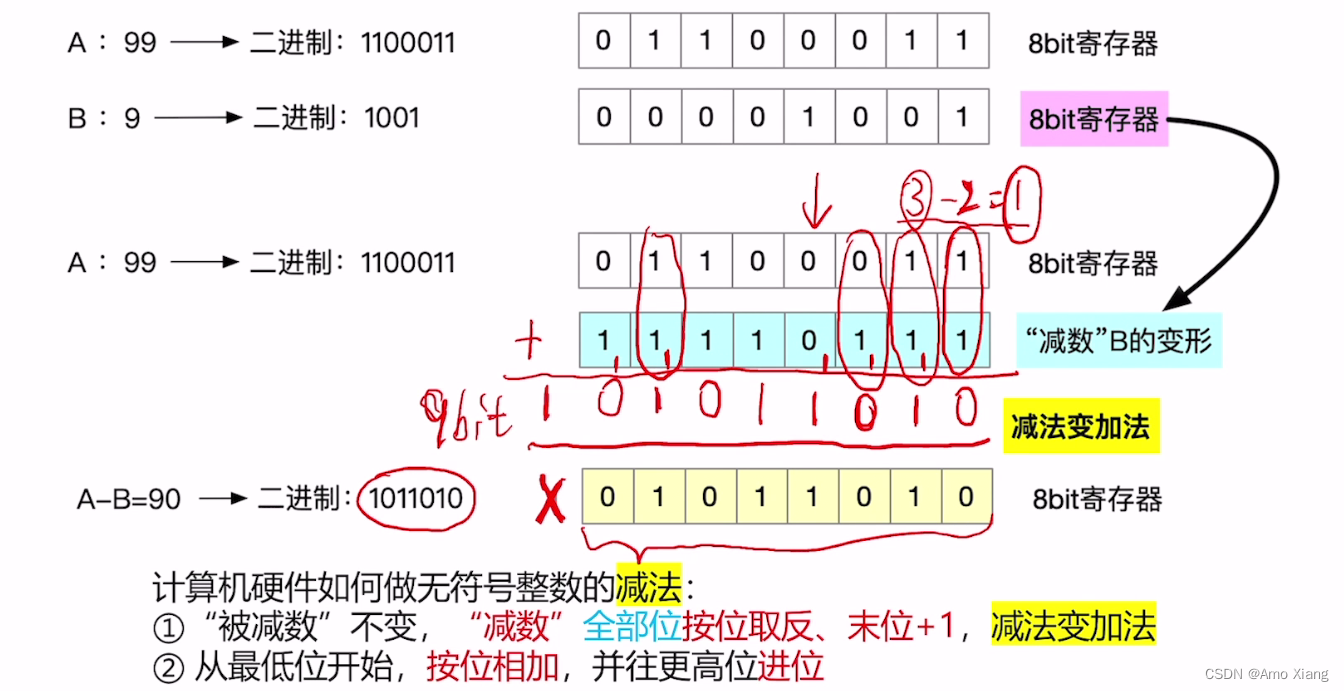
4.5 小结

五、带符号整数的表示和运算_原码、反码、补码

本小节总览：

5.1 带符号整数在计算机中的应用

5.2 带符号整数的表示

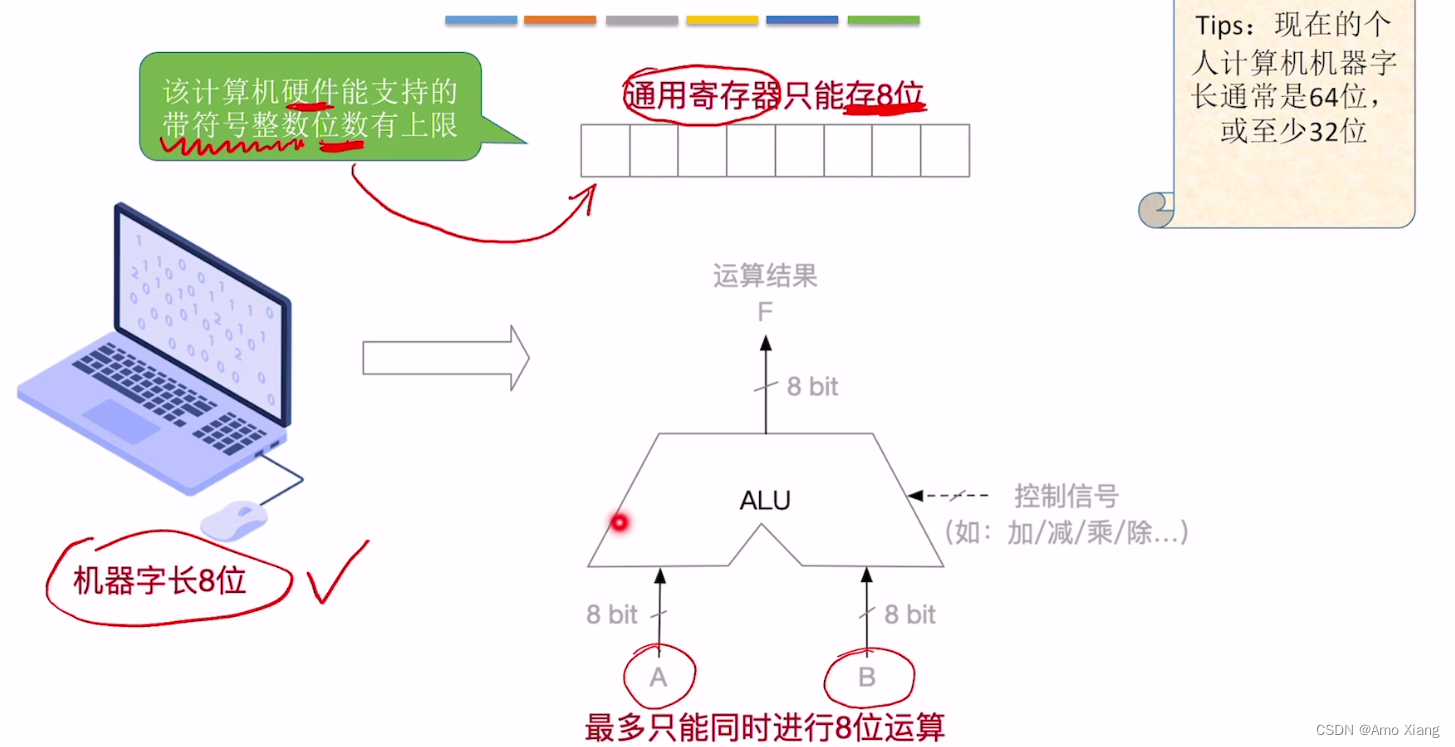
原码表示法：

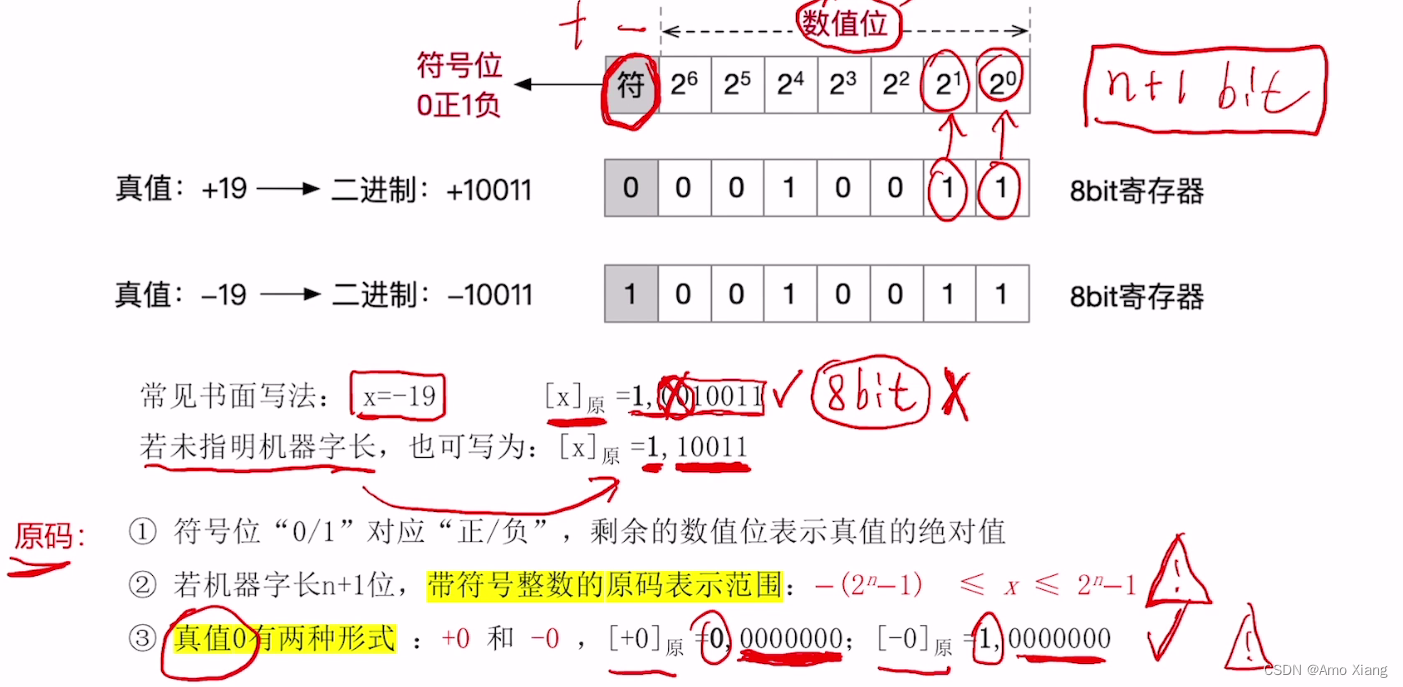
原码的缺点：

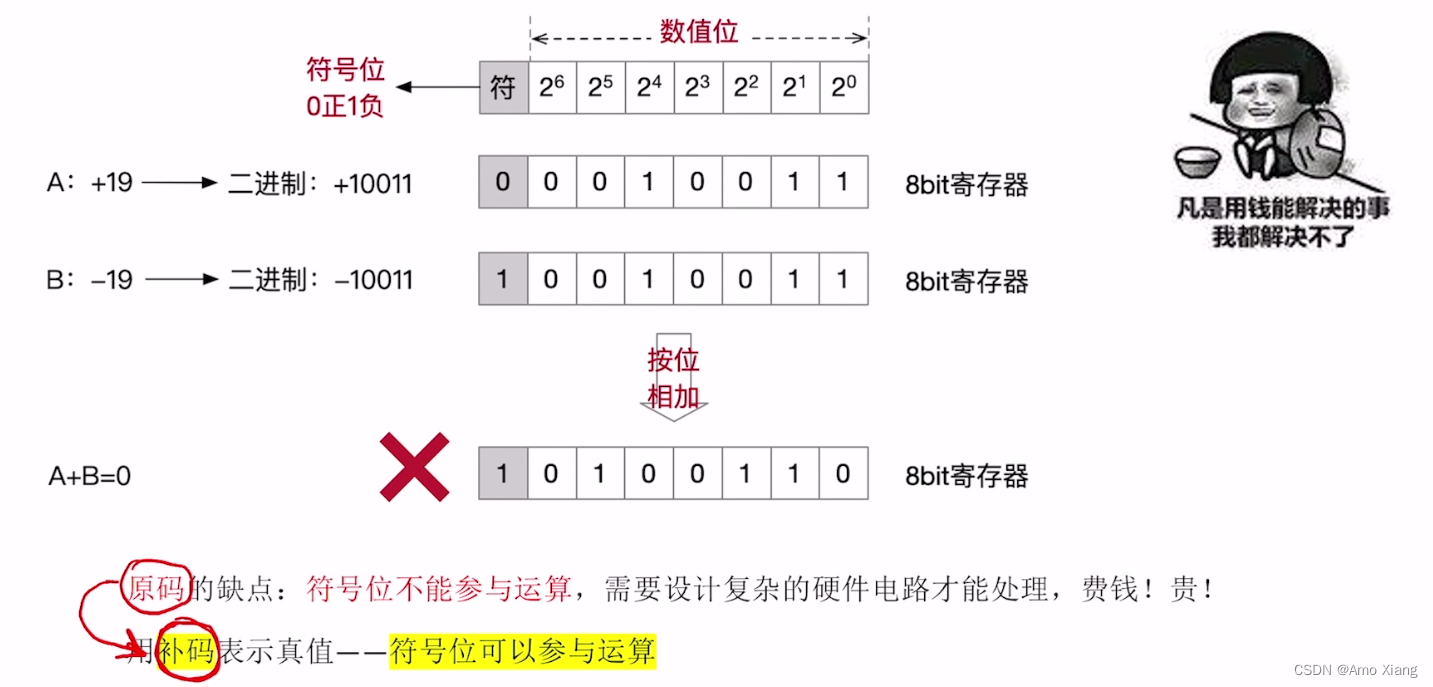
原码–>反码–>补码的转换（机算）

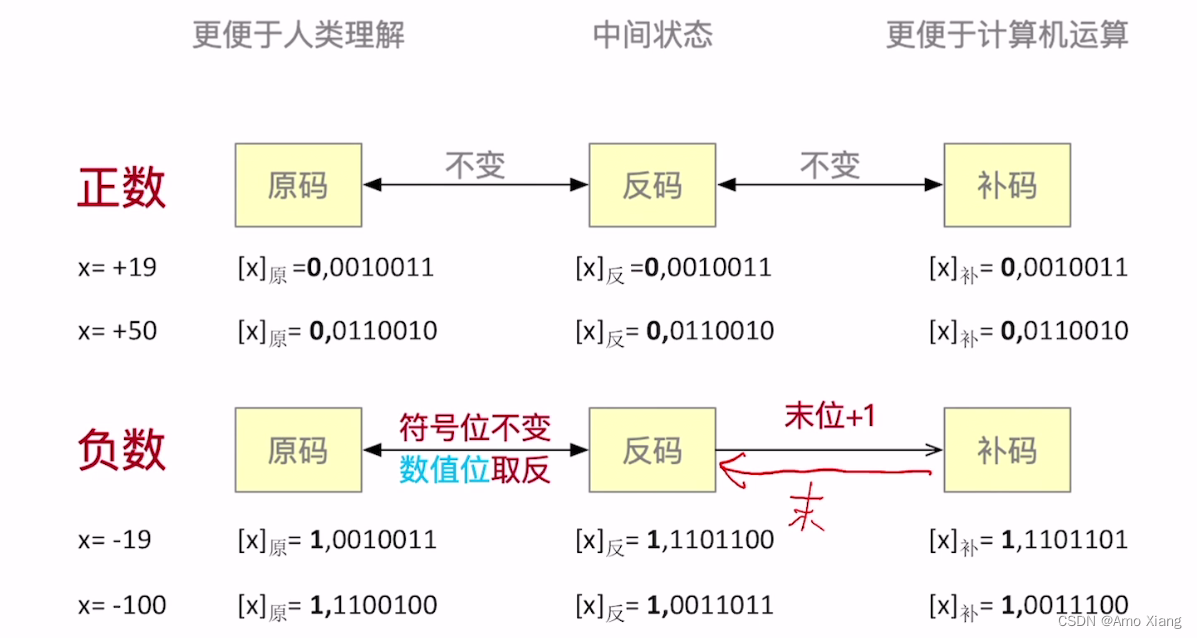
原码、补码快速转换技巧（手算）

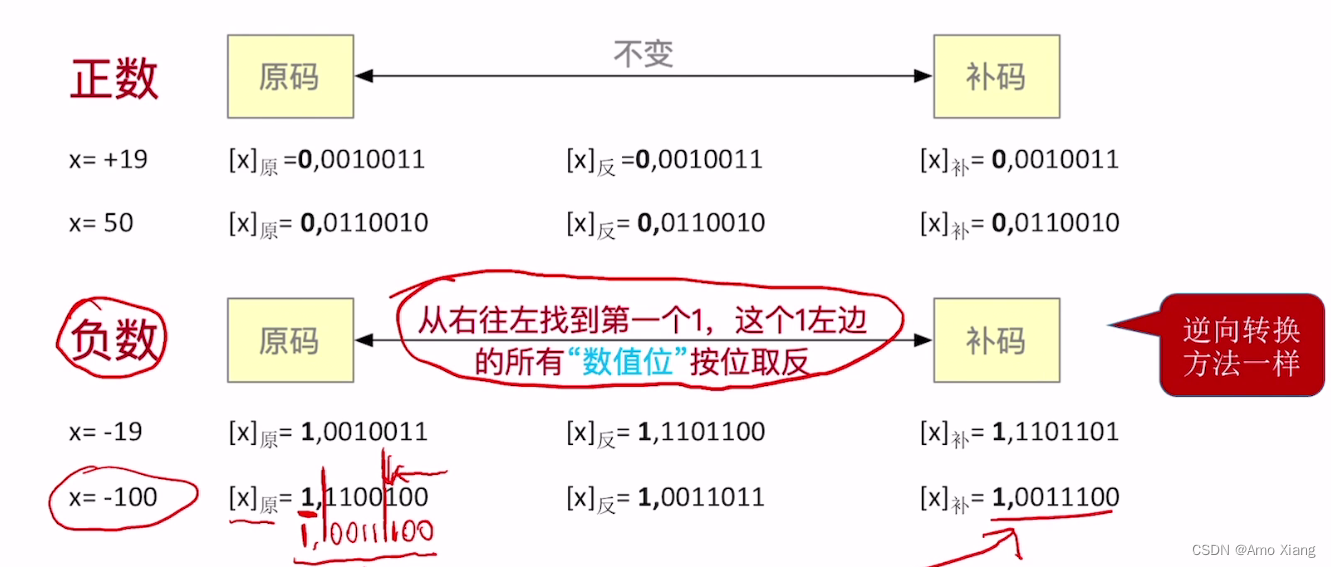
补码的加法运算（例1）：

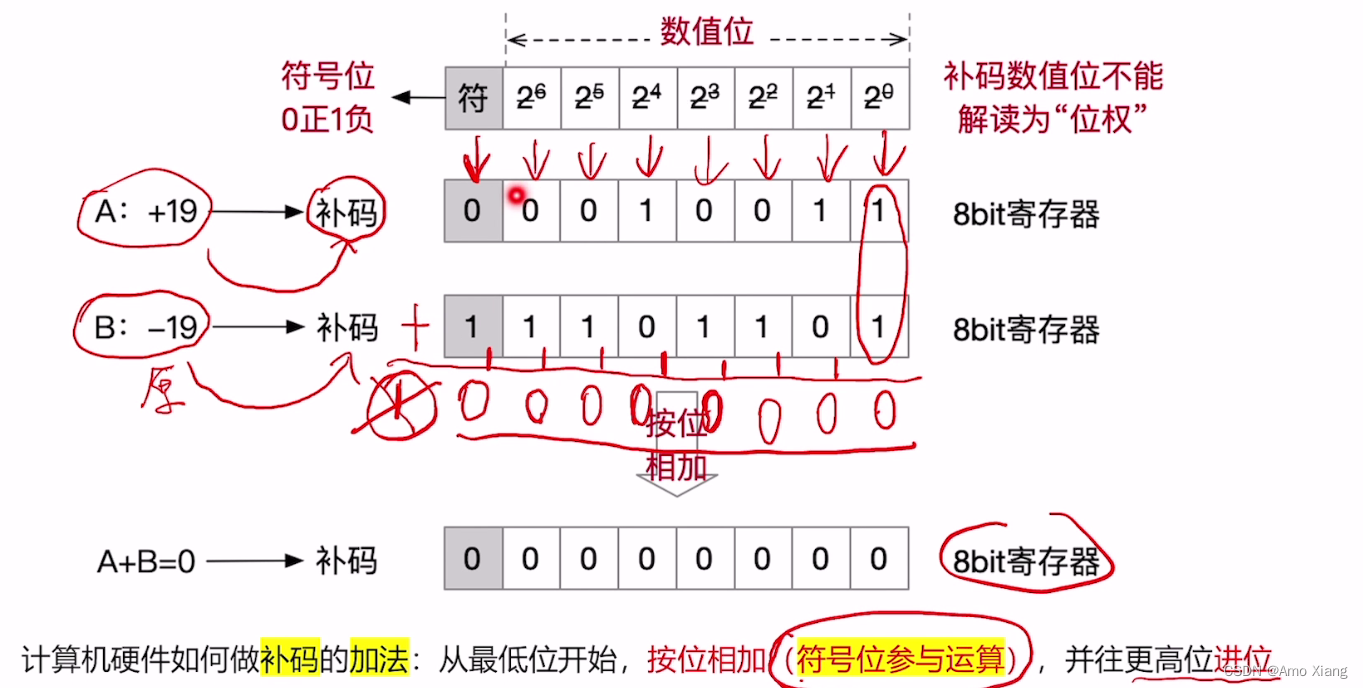
补码的加法运算（例2）：

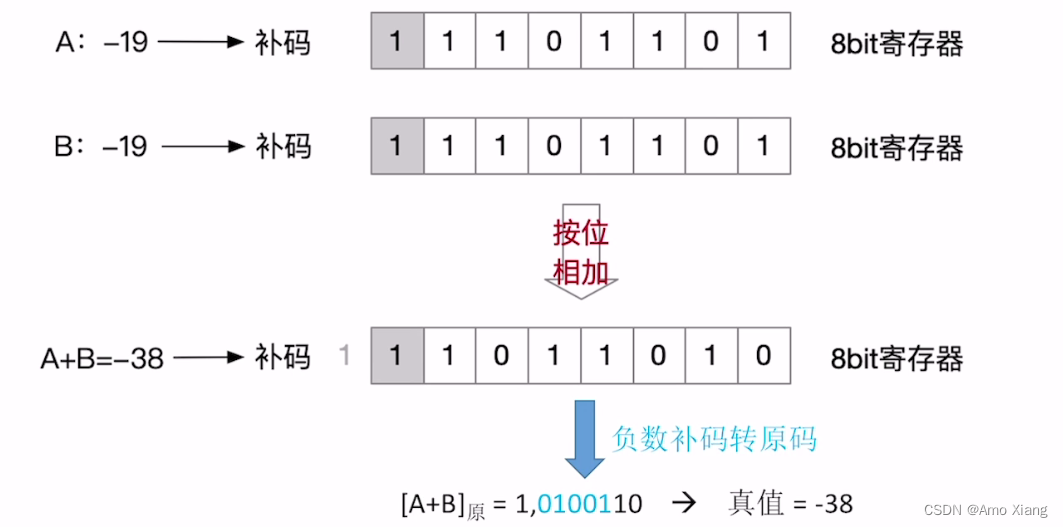
补码的减法运算：

补码的减法运算（例3）：

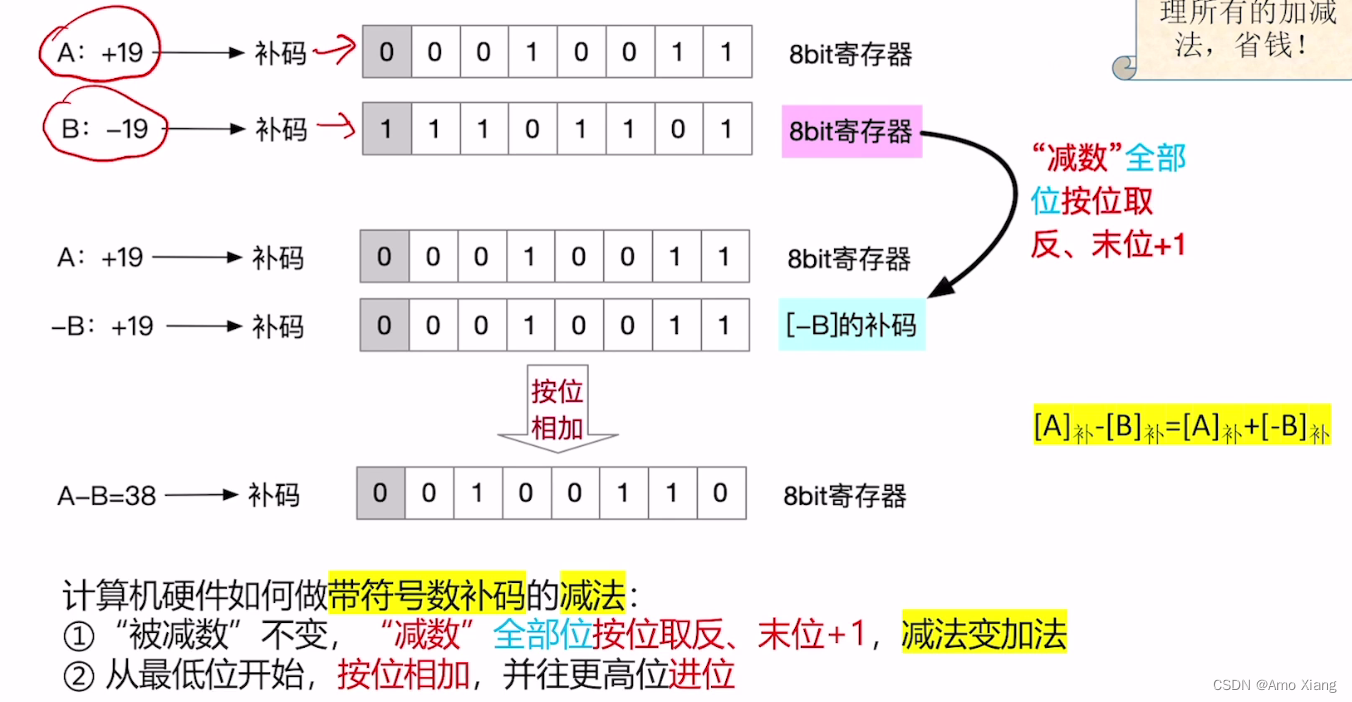
5.3 小结

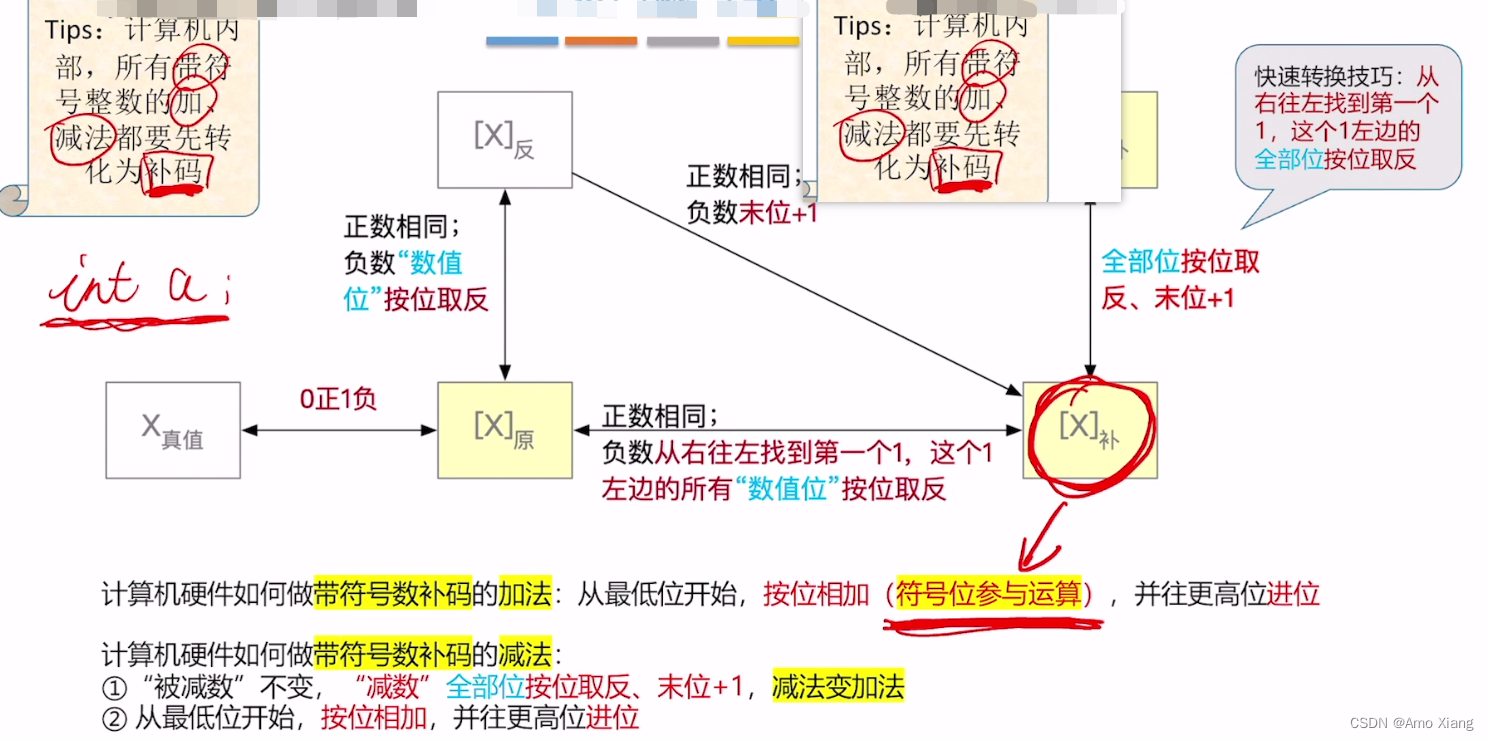
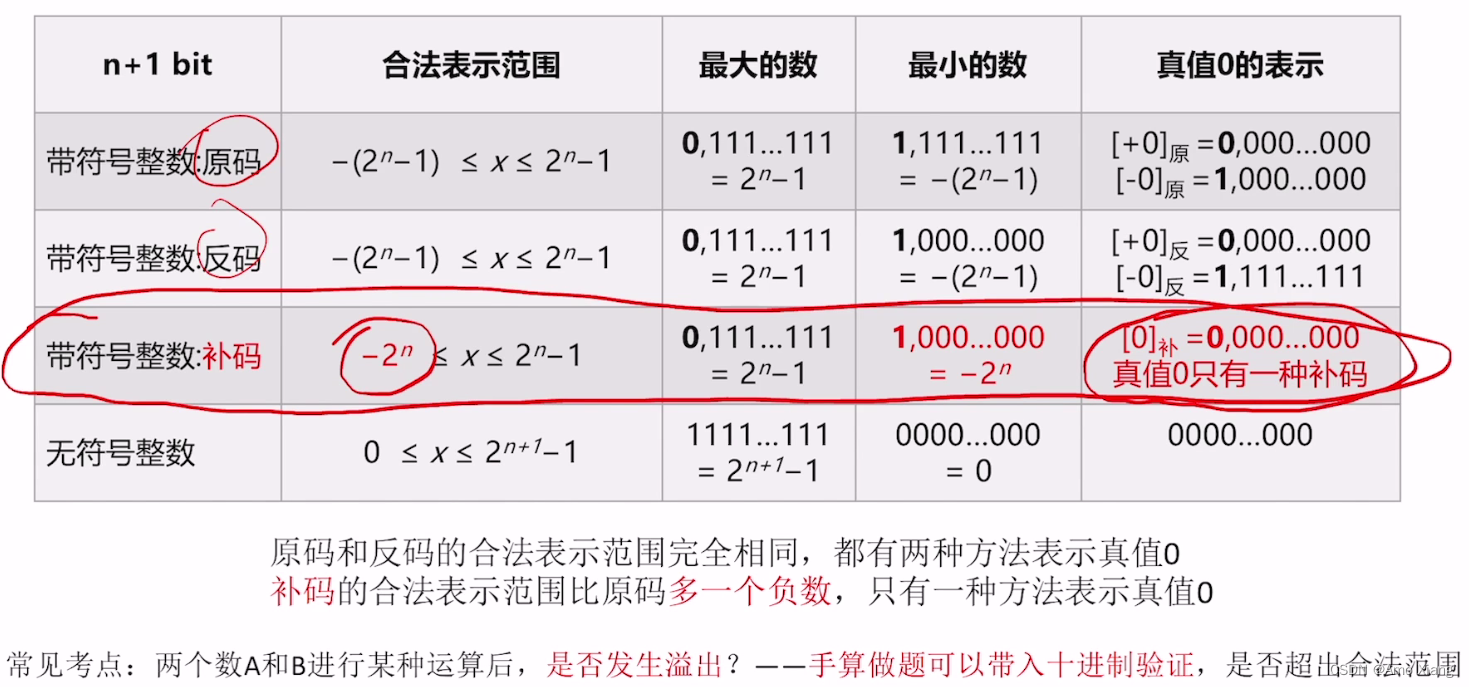
5.4 补充：原码、反码、补码的特性对比

各种码的基本特性总结：

5.5 移码

特点：

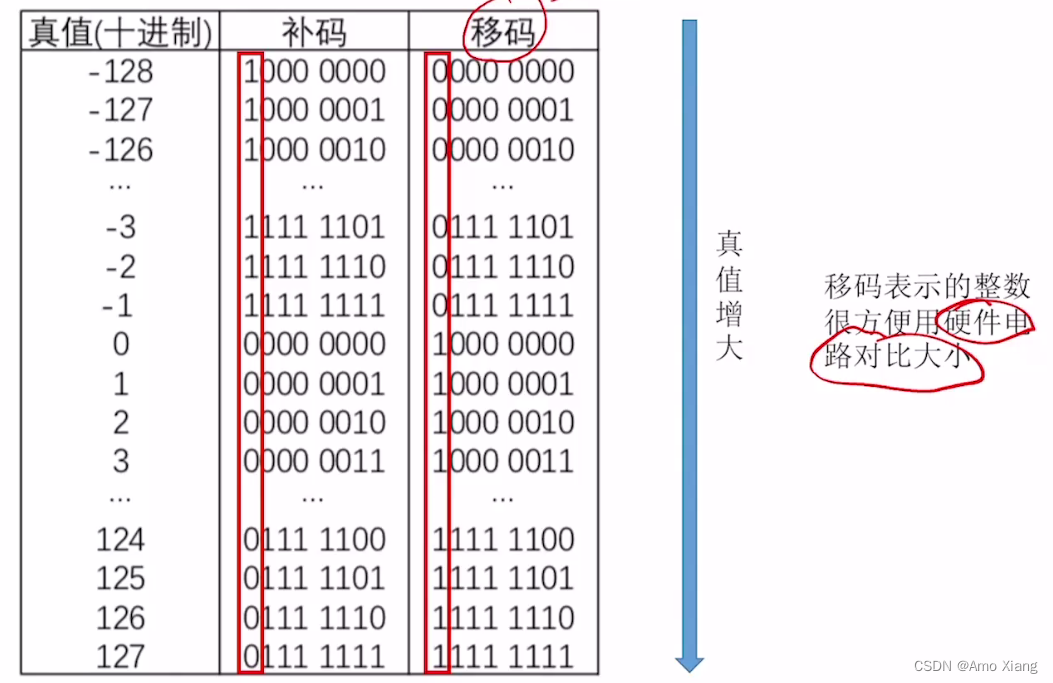
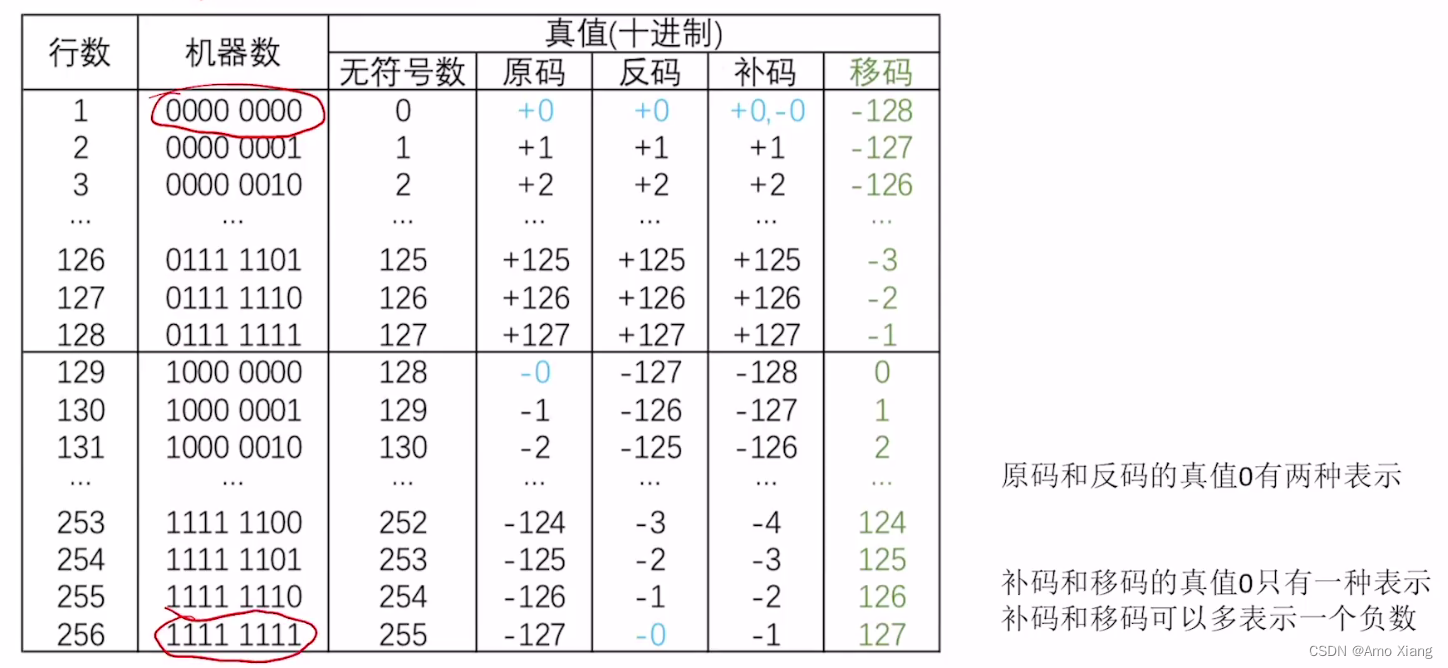
各种码的基本特性总结（补充）：

用几种码表示整数：

练习：

至此今天的学习就到此结束了，笔者在这里声明，笔者写文章只是为了学习交流，以及让更多学习C语言的读者少走一些弯路，节省时间，并不用做其他用途，如有侵权，联系博主删除即可。感谢您阅读本篇博文，希望本文能成为您编程路上的领航者。祝您阅读愉快！

---

    好书不厌读百回，熟读课思子自知。而我想要成为全场最靓的仔，就必须坚持通过学习来获取更多知识，用知识改变命运，用博客见证成长，用行动证明我在努力。
    如果我的博客对你有帮助、如果你喜欢我的博客内容，请 点赞、评论、收藏 一键三连哦！听说点赞的人运气不会太差，每一天都会元气满满呦！如果实在要白嫖的话，那祝你开心每一天，欢迎常来我博客看看。
 编码不易，大家的支持就是我坚持下去的动力。点赞后不要忘了 关注 我哦！