柱状图中最大的矩形

题目链接

用什么数据结构？

要得到柱状图中最大的矩形，我们就必须要知道对于每一个高度heights[i]，他所能勾勒出的矩形最大是多少（即宽度最大是多少）。

而对应到图上我们可以知道，要知道最大宽度，那就需要通过对下标的计算得到，因此要存储的也应该是每个高度对应的下标。

即：通过存储的下标索引找到对应的高度，同时快速计算出宽度，最终得到面积

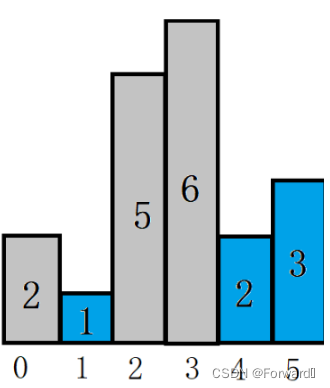
我们就拿上面的例子进行分析：

一开始遍历的柱形高度是2，但以这一高度所确定的矩形还不能确定其面积的最大值，因此继续遍历

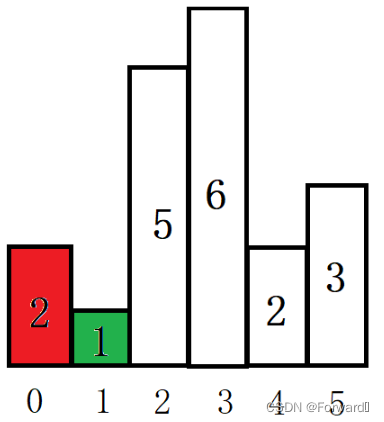
第二个柱形高度为1，此时这一高度所确定的最大矩形还不能确定。但是它前面的下标为0的柱形所确定的最大矩形就可以确定了。因为下标为1的这个柱形高度比下标为0的小，矮的卡在了高的后面，那么这个高的就不能向右扩展了。
- 这个时候，我们也就能计算下标为0的这一高度所能确定的最大矩形的面积了。同时，既然这一下标的高度已经确定，我们也就可以忽略这一下标代表的高度了，我们将其标灰。

第三个高度为5，由同样的分析可得，下标为2和下标为1的高度都不能确定其最大的矩形。继续遍历。
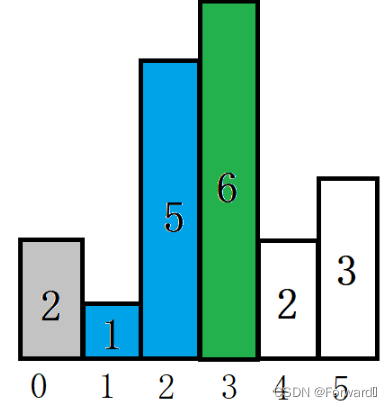
第四个高度为6，同样，高度为1,5,6的三个柱形也同样不能确定最大的矩形，继续便利。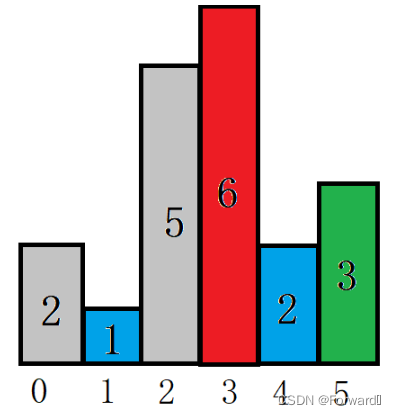
第五个高度为2，小于下标为3的高度，因此下标为3高度为6的柱形确定的最大矩形就知道了。面积size = 6 * (4-2-1) = 6，同时由于这个柱形已经计算，就将其忽略、标灰。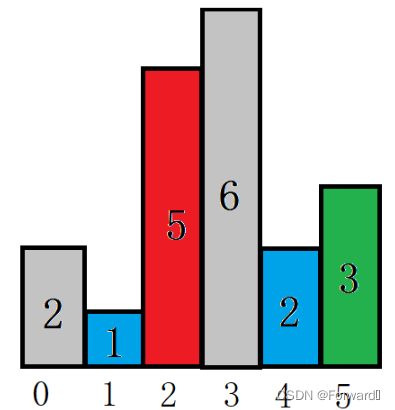
- 下标为4高度为2的柱形仍低于下标为2高度为5的柱形，因此下标为2高度为5的柱形确定的最大矩形也就知道了。面积size = 5 * (4-1-1) = 10，同时将这一柱形忽略、标灰。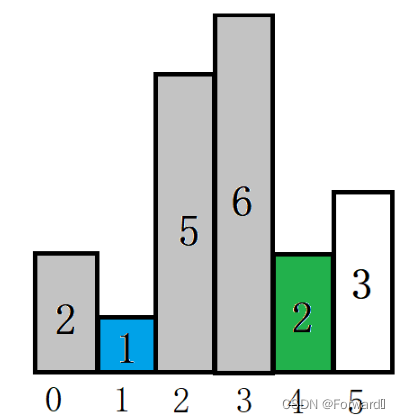
- 下标为4高度为2的柱形高于下标为1高度为1的柱形，因此这两个柱形仍不能确定其最大的矩形，继续遍历。
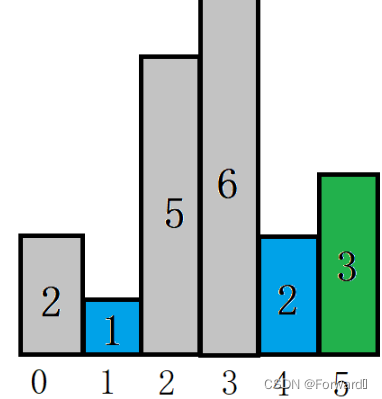
第六个的高度为3，由同样的分析，高度为1,2,3的柱形都不能确定其最大的矩形

此时我们就遍历完了整个heights数组，但是我们还有三个高度的最大矩形还没有确定，为了处理这三个数据，我们可以假设下标为6的柱形的高度为0（小于1都可以）

这样，下标为5高度为3的柱形就被夹在了两个较矮柱形的中间，其最大矩形也就确定了。size = 3 * (6-4-1) = 3

同理，下标为4高度为2的矩形面积为：size = 2 * (6-1-1) = 8

在这里插入图片描述

此时，只剩下下标为1高度为1的柱形，他是所有柱形中最低的柱形，所以它最大矩形的宽度就是整个数组的长度，因此面积size = 1 * 6 = 6

至此，每个柱形所确定的最大矩形都已经分析完毕。

由上面的分析我们可以得出以下结论：

存储下标时，我们是从左到右存储的，但是计算下标对应的高度所确定的矩形面积时，是从右向左计算的（例如是先计算高度为6的面积在计算高度为5的面积），这符合先入后出的特性，因此这一题我们要用到的数据结构是栈。
之所以能确定一个柱形的最大矩形，就是在他右边碰到了比他更低的柱形（因为这个更低的柱形限制了这个高柱形的扩张）。因此这个栈存放的下标对应的高度应该是单调非递减的（注意不是单调递增），只要碰到递减的情况，就说明可以计算栈顶元素所代表高度的矩形面积了。
这个栈之所以要单调非递减时要考虑到进栈元素等于栈顶元素的情况。如下图：

如果将栈设计为单调递增的，那么当进栈元素5入栈时，栈顶元素5就要出栈，并计算其面积，但问题是这个进栈元素5并不小于这个栈顶元素5，那么这个栈顶元素5所确定的最大矩形也就不能确定。
因此进栈元素等于栈顶元素时，栈顶元素不要出栈。即这个栈为单调非递减的。

考虑特殊情况（添加哨兵位）

情况一：计算宽度时栈空。如下图：

此时，栈中存储的下标为[0]，进栈下标对应的高度小于栈顶元素对应的高度，栈顶元素需要出栈，并计算其高度对应的最大矩形。现在问题来了，栈顶元素出栈后栈为空，没有下标用来计算宽度，这里就要用if(stackEmpty)来进行特殊处理，但显然这是不方便的。因此我们可以在heights数组的最前面加入一个高度0，这样我们就可以保证栈中始终留有数据（这个0不可能出栈），也就可以更加方便的计算宽度了。

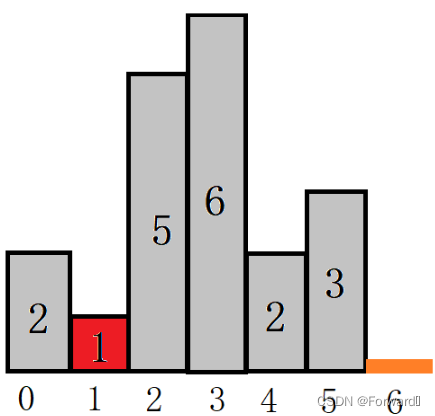
情况二：遍历完heights数组后，栈中还留有有效数据（部分柱形的最大矩形还未确定），如下图：

要计算出每个柱形的最大矩形，也就是要将栈中的每个下标都出栈，而要确保每个下标都可以出栈，那就要保证进栈下标代表的高度要小于栈中元素对应的高度，因此我们可以在heights数组的末尾再加上一个0，这样就可以保证在遍历完heights数组的同时，每个高度的最大矩形都可以被计算了。

这两个高度为0，站在数组两边的柱形，就是我们常说的哨兵

实现代码

int largestRectangleArea(int* heights, int heightsSize){
    //添加哨兵位：
    heights = (int*)realloc(heights, sizeof(int) * (heightsSize + 2));
    heights[heightsSize + 1] = 0;	//尾部添加0
    for (int i = heightsSize; i > 0; i--)
        heights[i] = heights[i - 1];
    heights[0] = 0;	//头部添加0

    int *stack = (int*)malloc(sizeof(int) * (heightsSize + 2));
    int top = 0;
    int ret_size = 0;

    for (int i = 0; i < heightsSize + 2; i++)
    {
        //当栈不为空并且进栈元素小于栈顶元素
        //就开始计算矩形面积
        while (top != 0 && heights[i] < heights[stack[top - 1]])
        {
            //栈顶元素出栈
            int high_index = stack[top - 1];
            top--;

            int wide = i - stack[top - 1] - 1;	//宽度
            int high = heights[high_index];	//高度
            ret_size = ret_size > wide * high ? ret_size : wide * high;
        }
		
        //计算完成后或者没有进入循环，进栈元素都要入栈
        stack[top++] = i;
    }

    free(stack);	//释放栈

    return ret_size;
}