题目、解析和代码

题目：给定一个单链表，判断其中是否有环的存在
解析：这里使用两个遍历速度不一样的结点进行判断，一个慢结点从首结点开始遍历，这个结点每次只遍历一个结点；一个快结点从第二个结点进行遍历，一次遍历两个结点。
若是链表中存在环，那么必然在某个结点处相遇；若是没有环，那么尾结点后继指针指向空。
LinkedListChainTest.c代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct operatorNodeStruce {
    int data;
    struct operatorNodeStruce* next;
}operatorNode;

int main(int argc, char *argv[]) {
    if(argc == 1){
        printf("请输入链表中结点个数和环的接连位置\n");
        return 0;
    }else if(argc == 2){
        printf("请输入环的接连位置,负数表示没有环\n");
        return 0;
    }else if(argc > 3){
        printf("参数不能大于3个\n");
        return 0;
    }
    int nodeNumber = atoi(argv[1]);
    int chainNodeIndex = atoi(argv[2]);
    if(chainNodeIndex>nodeNumber){
        printf("环的接连位置应该小于链表中结点个数\n");
        return 0;
    }
    operatorNode *head = NULL;
    operatorNode *storeNode = NULL;
    int i=1;
    // 创建链表，这个链表有nodeNumber个结点
    for(;i<=nodeNumber;i++){
        operatorNode *newNode = (operatorNode *)malloc(sizeof(operatorNode));
        newNode->next = NULL;
        newNode->data = i;
        if(head == NULL){
            head = newNode;
            storeNode = head;
        }else{
            storeNode->next = newNode;
        }
        if(storeNode -> next != NULL){
            storeNode = storeNode -> next;
        }
    }

    //把最后一个结点的后继指针next指向第chainNodeIndex个结点，这样的话才能形成环
    operatorNode *chainNodeBefore = NULL;
    operatorNode *node= NULL;
    if(chainNodeIndex > 0){
        for(int i=0;i<chainNodeIndex;i++){
            if(node == NULL){
                node = head;
            }
            chainNodeBefore = node;
            node = node->next;
        }
    }
    storeNode->next = chainNodeBefore;

    // 使用快慢结点法来判断是否有环，slowNode从第一个结点开始往后遍历，每次只遍历一个结点；fastNode从第二个结点开始往后遍历，每次遍历二个结点；
    // 要是有环，快结点（fastNode）一定能够在某个结点处跟慢结点（slowNode）相遇
    operatorNode *fastNode = NULL;
    if(head->next != NULL){
        fastNode = head->next;
    }
    operatorNode *slowNode = head;
    while(true){
        if(fastNode== NULL){
            printf("无环\n");
            return 0;
        }else if(fastNode->next == NULL){
            printf("无环\n");
            return 0;
        }else if(fastNode->next->next == NULL){
            printf("无环\n");
            return 0;
        }else{
            if(slowNode == fastNode){
                printf("有环\n");
                return 0;
            }
            slowNode = slowNode->next;
            fastNode = fastNode->next->next;
        }
    }
    return 0;
}

gcc LinkedListChainTest.c -o LinkedListChainTest进行编译。

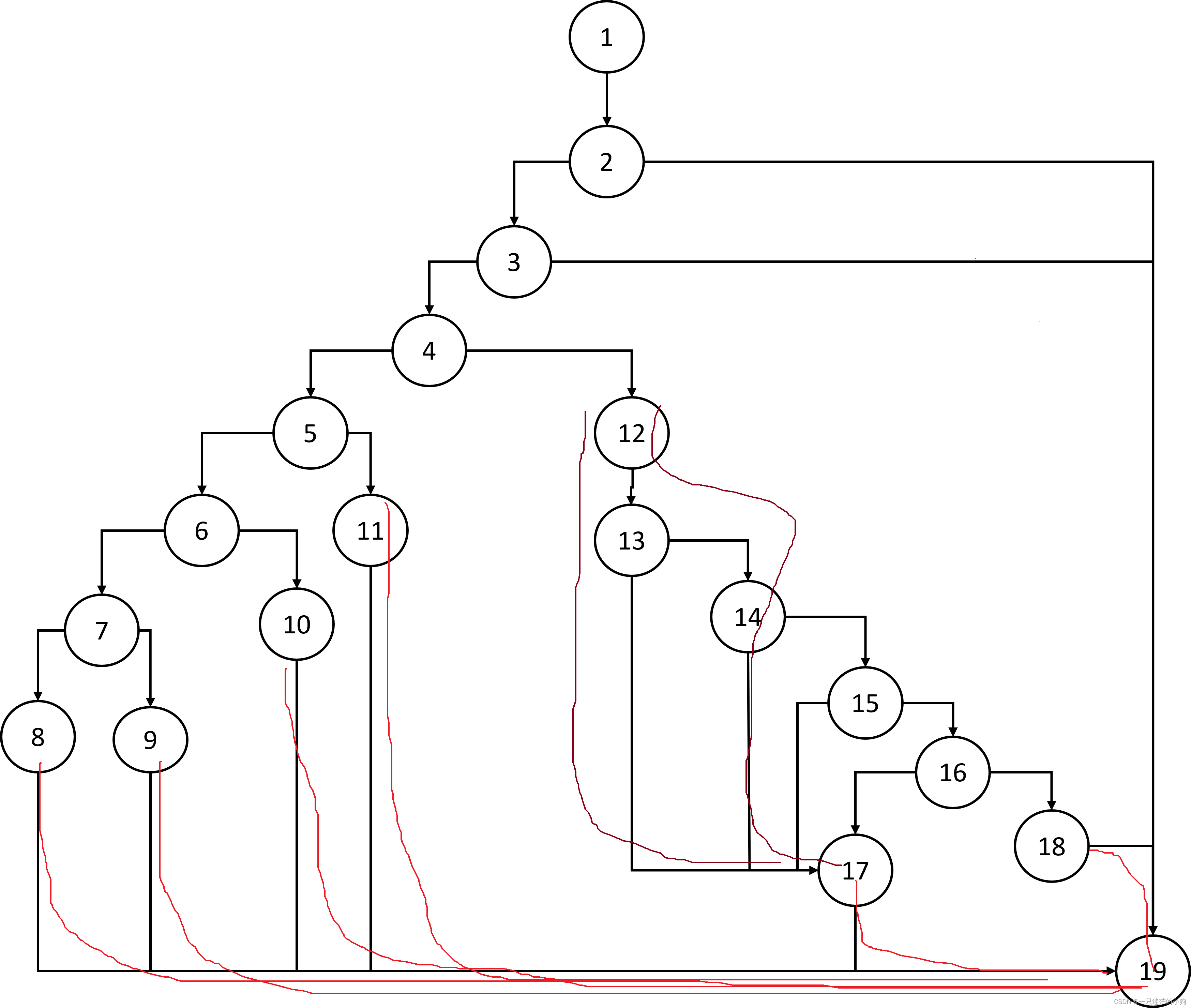
./LinkedListChainTest 6 4表示这个链表有6个结点，最后一个结点后继指针指向第4个结点，就像下图所示。

./LinkedListChainTest 7 2表示这个链表有7个结点，最后一个结点后继指针指向第2个结点，就像下图所示。

./LinkedListChainTest 8 3表示这个链表有8个结点，最后一个结点后继指针指向第3个结点，就像下图所示。

遍历解析

以./LinkedListChainTest 6 4为例进行解析。

如上图，蓝色圆心虚线箭头为慢结点（slowNode）所在位置的标识。

如上图，绿色实心箭头为快结点（fastNode）所在位置的标识。

刚开始的实例图如下：

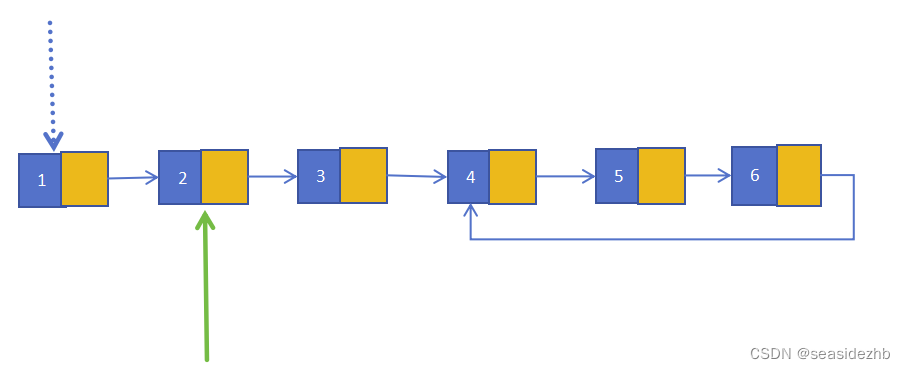
第1次遍历之后，慢结点在第2个结点处，快结点在第4个结点处：

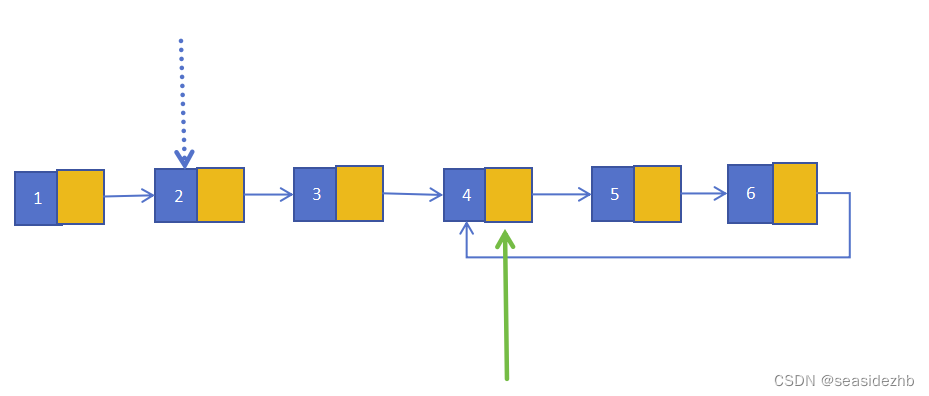
第2次遍历之后，慢结点在第3个结点处，快结点在第6个结点处：

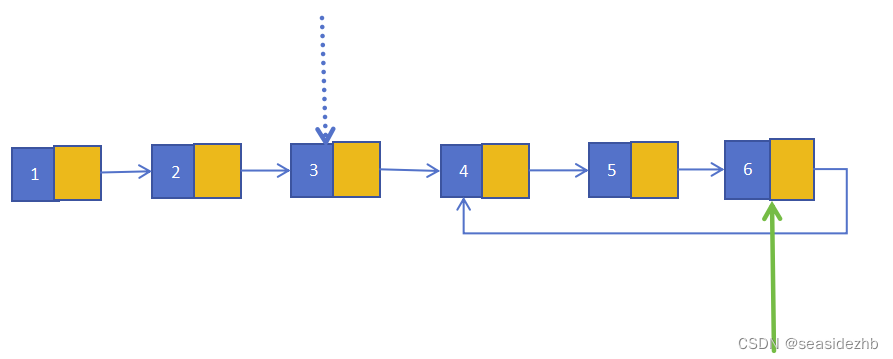
第3次遍历之后，慢结点在第4个结点处，快结点在第5个结点处：

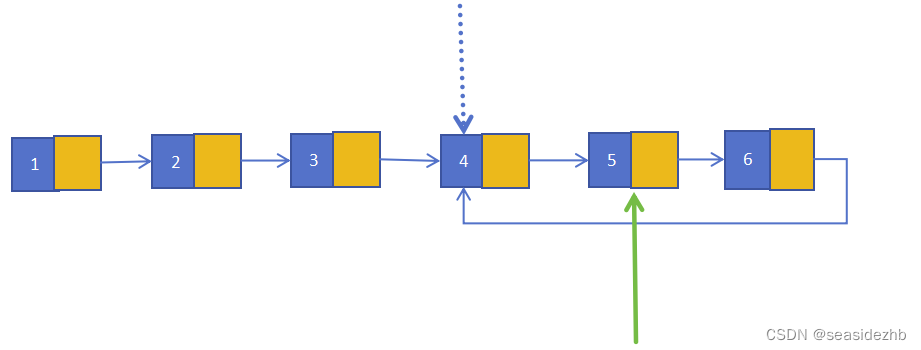
第4次遍历之后，慢结点在第5个结点处，快结点在第5个结点处，可以判定有环：

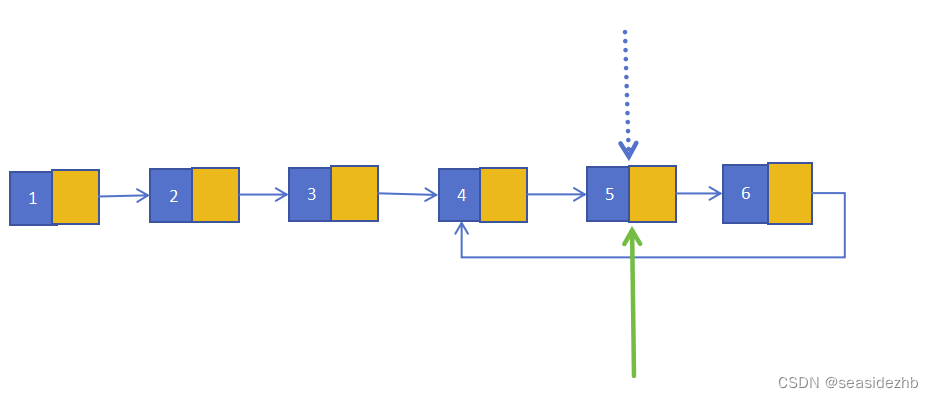
复杂度分析

结点个数	环的接连位置	快结点在环中所落位置	遍历次数
6	1	2、4、6	5
6	2	3、5、2、4、6	4
6	3	4、6	3
6	4	5、4、6	5
6	5	6	5
6	6	6	5
7	1	1、3、5、7、2、4、6	6
7	2	2、4、6	5
7	3	3、5、7、4、6	4
7	4	4、6	3
7	5	5、7、6	5
7	6	6	5
7	7	6	6

若链表中有2n(n>=1,是正整数，2n为偶数）个结点：

那么若环的连接位置x不大于n，那么遍历次数为2n-x；
若是环的连接位置x大于n，则最多遍历次数小于等于2n-1，还没有总结出来公式。

若链表中有2n+1(n>=1,是正整数，2n+1为偶数）个结点：

那么环的连接位置x若不大于n+1，那么遍历次数为2n+1-x；
若是环的连接位置x大于n，则最多遍历次数小于等于2n+1，还没有总结出来公式。

若是没有环的话，最多遍历次数是n/2。
综上所述，最好时间复杂度和最坏时间复杂度都是O(n)，平均时间复杂度也是O(n)。
而空间复杂度是O(1)，因为除了存储变量的必要空间，没有申请额外的空间。
因为需要更好地分析时间复杂度，所以，我把代码修改成下方所示：

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

typedef struct operatorNodeStruce {
    int data;
    struct operatorNodeStruce* next;
}operatorNode;

int main(int argc, char *argv[]) {
    if(argc == 1){
        printf("请输入链表中结点个数和环的接连位置\n");
        return 0;
    }else if(argc == 2){
        printf("请输入环的接连位置,负数表示没有环\n");
        return 0;
    }else if(argc > 3){
        printf("参数不能大于3个\n");
        return 0;
    }
    int nodeNumber = atoi(argv[1]);
    int chainNodeIndex = atoi(argv[2]);
    if(chainNodeIndex>nodeNumber){
        printf("环的接连位置应该小于链表中结点个数\n");
        return 0;
    }
    operatorNode *head = NULL;
    operatorNode *storeNode = NULL;
    int i=1;
    // 创建链表，这个链表有nodeNumber个结点
    for(;i<=nodeNumber;i++){
        operatorNode *newNode = (operatorNode *)malloc(sizeof(operatorNode));
        newNode->next = NULL;
        newNode->data = i;
        if(head == NULL){
            head = newNode;
            storeNode = head;
        }else{
            storeNode->next = newNode;
        }
        if(storeNode -> next != NULL){
            storeNode = storeNode -> next;
        }
    }


    //把最后一个结点的后继指针next指向第chainNodeIndex个结点，这样的话才能形成环
    operatorNode *chainNodeBefore = NULL;
    operatorNode *node= NULL;
    if(chainNodeIndex > 0){
        for(int i=0;i<chainNodeIndex;i++){
            if(node == NULL){
                node = head;
            }
            chainNodeBefore = node;
            node = node->next;
        }
    }
    storeNode->next = chainNodeBefore;



    // 使用快慢结点法来判断是否有环，slowNode从第一个结点开始往后遍历，每次只遍历一个结点；fastNode从第二个结点开始往后遍历，每次遍历二个结点；
    // 要是有环，快结点（fastNode）一定能够在某个结点处跟慢结点（slowNode）相遇
    operatorNode *fastNode = NULL;
    if(head->next != NULL){
        fastNode = head->next;
    }
    operatorNode *slowNode = head;
    int chainNodetimes = 0;
    while(true){
        if(chainNodetimes != 0){
            printf("fastNode data:%d\tslowNode data: %d\n",fastNode->data,slowNode->data);
        }
        if(fastNode== NULL){
            printf("无环\n");
            return 0;
        }else if(fastNode->next == NULL){
            printf("无环\n");
            return 0;
        }else if(fastNode->next->next == NULL){
            printf("无环\n");
            return 0;
        }else{
            if(slowNode == fastNode){
                printf("循环次数：%d\n",chainNodetimes);
                printf("有环\n");
                return 0;
            }
            slowNode = slowNode->next;
            fastNode = fastNode->next->next;
            chainNodetimes++;
        }
    }
    return 0;
}