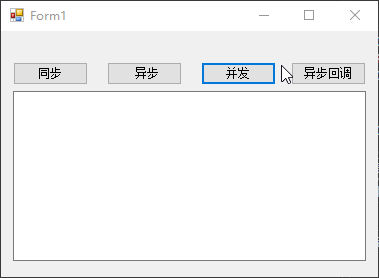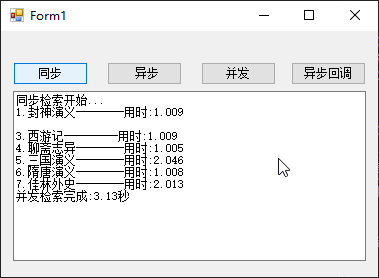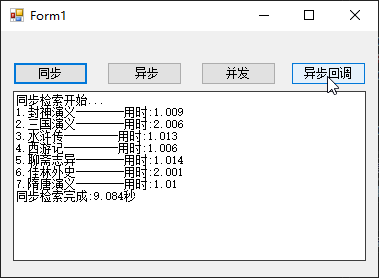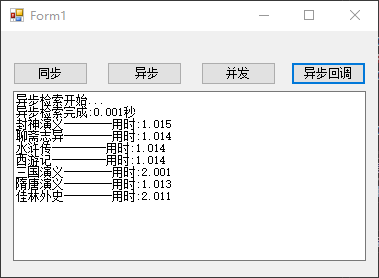
有许多方法可以把对象堆起来成为一个集合（Collection），比如放入数组、堆栈或散列表中。若用户直接从这些数据结构中取出对象，则需要知道具体是存在什么数据结构中（如栈就用peek，数组[]）。迭代器能够让客户遍历你的对象而又无法窥视你存储对象的方式。

对象村餐厅和煎饼屋合并了，它们有着不同的菜单列表，但菜单项基础都是一样的。

class MenuItem
{
private:
	string name;
	string description;
	bool vegetarian;
	double price;

public:
	MenuItem(string name, string description, bool vegetarian, double price)
	{
		this->name = name;
		this->description = description;
		this->vegetarian = vegetarian;
		this->price = price;
	}

	string getName()
	{
		return name;
	}

	string getDescription()
	{
		return description;
	}

	bool isVegetarian()
	{
		return vegetarian;
	}

	double getpPrice()
	{
		return price;
	}
};

下面就写Java代码了，改成C++一时半会还是做不过来。

public class PancakeHouseMenu
{
	ArrayList menuItems;

	public PancakeHouseMenu()
	{
		menuItems = new ArrayList();

		addItem("K&B's Pancake Breakfast", "Pancakes with scrambled eggs, and toast", true, 2.99);
	}

	public void addItem(String name, String description, boolean vegetarian, double price)
	{
		MenuItem menuItem = new MenuItem(name, description, vegetarian, price);
		menuItems.add(menuItem);
	}

	public ArrayList getMenuItems()
	{
		return menuItems;
	}
};


/ ********************************************************/
public class DinerMenu
{
	static final int MAX_ITEMS = 6;
	int numberOfItems = 0;
	MenuItem[] menuItems;

	public DinerMenu()
	{
		menuItems = new MenuItem[MAX_ITEMS];

		addItem("Vegetarian BLT", "Fakin Bacon", true, 2.99);
	}

	public void addItem(String name, String description, boolean vegetarian, double price)
	{
		MenuItem menuItem = new MenuItem(name, description, vegetarian, price);
		if (numberOfItems >= MAX_ITEMS)
		{
			System.err.println("Sorry, menu is full! Can't add item to menu");
		}
		else
		{
			menuItems[numberOfItems++] = menuItem;
		}
	}

	public MenuItem[] getMenuItems()
	{
		return menuItems;
	}
};

这两种不同的菜单表现方式，会使得女招待需要知道菜单的实现细节，才能对菜单进行遍历。

PancakeHouseMenu pancakeHouseMenu = new PancakeHouseMenu();
ArrayList breakfastItems = pancakeHouseMenu.getMenuItems();

for breakfastItems.size()
MenuItem menuItem = (MenuItem)breakfastItems.get(i);


/ ******************************************************************* /
DinerMenu dinerMenu = new DinerMenu();
MenuItem[] lunchItems = DinerMenu.getMenuItems();

for lunchItems.size()
MenuItem menuItem = lunchItems[i];

如果还有第三家餐厅以不同的实现出现，我们就需要有三个循环。

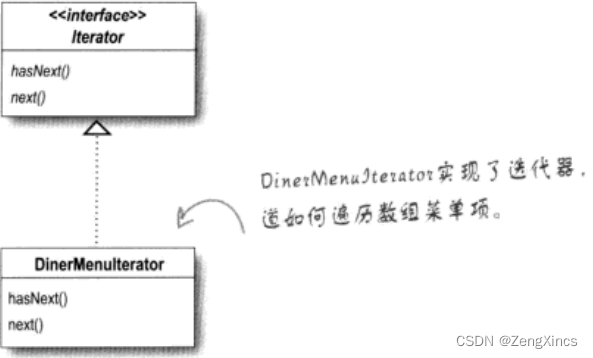
因此，我们需要创建一个对象（迭代器），封装“遍历集合内的每个对象的过程”。

Iterator iter = breakfastItems.createIterator();

while (iter.hasNext())
{
	MenuItem menuItem = (MenuItem)iter.next();
}

 当我们拥有迭代器接口后，我们就可以为各种对象集合实现迭代器