时序预测 | MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)

预测效果

基本介绍

Matlab实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测
TSO-XGBoost，金枪鱼算法优化，XGBoost，时间序列预测。
1.data为数据集，单变量时间序列数据集，优化参数（最大迭代次数，深度，学习率），
2.MainTSO_XGboostTS.m为主程序文件，其他为函数文件，无需运行。
3.命令窗口输出R2、MAE、MAE和RMSEP等评价指标，可在下载区获取数据和程序内容。
注意程序和数据放在一个文件夹，文件夹不可以XGBoost命名，因为有函数已经用过，运行环境为Matlab2018及以上。

• xgboost是属于boosting家族，在目标函数中使用了二阶泰勒展开并加入了正则，在决策树的生成过程中采用了精确贪心的思路，寻找最佳分裂点的时候，使用了预排序算法，对所有特征都按照特征的数值进行预排序，然后遍历所有特征上的所有分裂点位，计算按照这些候选分裂点位分裂后的全部样本的目标函数增益，找到最大的那个增益对应的特征和候选分裂点位，从而进行分裂。
• 这样一层一层的完成建树过程， xgboost训练的时候，是通过加法的方式进行训练，也就是每一次通过聚焦残差训练一棵树出来，最后的预测结果是所有树的加和表示。

程序设计

• 完整源码和数据下载地址：MATLAB实现基于TSO-XGBoost金枪鱼算法优化XGBoost的时间序列预测(多指标评价)

%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  优化算法
[Best_pos, Best_score, curve, avcurve] = TSO(pop, Max_iteration, lb, ub, dim, fun);

%%  获取最优参数
num_trees = Best_pos(1, 1);         % 迭代次数
%params.max_depth = Best_pos(1, 2);  % 树的深度
params.max_depth = 18;  % 树的深度
params.eta = Best_pos(1, 3);        % 学习率

%%  建立模型
model = xgboost_train(p_train, t_train, params, num_trees);

%%  预测
t_sim1 = xgboost_test(p_train, model);
t_sim2 = xgboost_test(p_test , model);

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1', ps_output);
T_sim2 = mapminmax('reverse', t_sim2', ps_output);

%% V. 评价指标
%%  均方根误差 RMSE
error1 = sqrt(sum((T_sim1 - T_train).^2)./M);
error2 = sqrt(sum((T_test - T_sim2).^2)./N);

%% 决定系数
R1 = rsquare(T_train,T_sim1);
R2 = rsquare(T_test,T_sim2);

MAE1 = mean(abs(T_train - T_sim1));
MAE2 = mean(abs(T_test - T_sim2));
%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1)./T_train));
MAPE2 = mean(abs((T_test - T_sim2)./T_test));
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
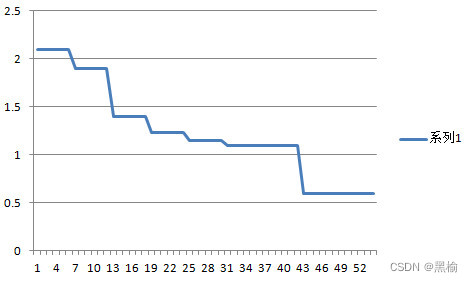
%%  适应度曲线
figure
plot(1 : length(curve), curve, 'LineWidth', 1.5);
title('TSO适应度变化曲线', 'FontSize', 13);
xlabel('迭代次数', 'FontSize', 10);
ylabel('适应度值', 'FontSize', 10);
grid on

aa=0.7;
z=0.05;
while Iter<Max_iter
    C=Iter/Max_iter;
    a1=aa+(1-aa)*C;
    a2=(1-aa)-(1-aa)*C;
    for i=1:size(T,1)
        
        Flag4ub=T(i,:)>ub;
        Flag4lb=T(i,:)<lb;
        T(i,:)=(T(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
        
        fitness(i)=fobj(T(i,:));
        
        if fitness(i)<Best_score
            Best_score=fitness(i);  Best_pos=T(i,:);
        end
    end
    

    
    C_old=T;  fit_old=fitness;
    %-------------------------------------------------
    
    t=(1-Iter/Max_iter)^(Iter/Max_iter);
    
    
    if rand<z
        T(1,:)= (ub-lb)*rand+lb;
    else
        if  0.5<rand
            r1=rand;
            Beta=exp(r1*exp(3*cos(pi*((Max_iter-Iter+1)/Max_iter))))*(cos(2*pi*r1));
            if  C>rand
                T(1,:)=a1.*(Best_pos+Beta*abs(Best_pos-T(1,:)))+a2.*T(1,:); %Equation (8.3)
                
            else
                IndivRand=rand(1,dim).*(ub-lb)+lb;
                T(1,:)=a1.*(IndivRand+Beta*abs(IndivRand-
                T(1,:)=Best_pos+rand(1,dim).*(Best_pos-T(1,:))+TF.*t^2.*(Best_pos-T(1,:));%Equation (9.1)
            else
                T(1,:) =TF.* t^2.*T(1,:);%Equation (9.2)
            end
            
        end
        
    end
    
    for i=2:pop
        if rand<z
            
            T(i,:)= (ub-lb)*rand+lb;
        else
            if  0.5<rand
                r1=rand;

                    T(i,:)=a1.*(Best_pos+Beta*abs(Best_pos-T(i,:)))+a2.*T(i-1,:);%Equation (8.4)
                else
                    
                    IndivRand=rand(1,dim).*(ub-lb)+lb;
                    T(i,:)=a1.*(IndivRand+Beta*abs(IndivRand-T(i,:)))+a2.*T(i-1,:);%Equation (8.2)
                end
            else
                TF = (rand>0.5)*2-1;
                if 0.5>rand
                    T(i,:)=Best_pos+rand(1,dim).*(Best_pos-T(i,:))+TF*t^2.*(Best_pos-T(i,:)); %Equation (9.1)
                else
                    T(i,:) = TF*t^2.*T(i,:);%Equation (9.2)
                end
            end
        end
    end
    
    Iter=Iter+1;
    curve(Iter)=Best_score;
    %curve(Iter) = GBestF;
   avcurve(Iter) = sum(curve) / length(curve);
   disp(['第' num2str(Iter) '次迭代适应度值：' num2str(Best_score)])
end

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/124693040?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/124864369?spm=1001.2014.3001.5502