比较重合点的排斥能

news2024/11/14 3:14:40

( A, B )---3*30*2---( 1, 0 )( 0, 1 )

让网络的输入只有3个节点，AB训练集各由5张二值化的图片组成，让A中有2个1，B中有1个1，有一个点重合，排列组合，统计迭代次数并排序。

得到数据

构造平均列A

构造平均列AB1

构造平均列AB2

差值结构

A-B

迭代次数

排斥能EA

排斥能EAB1

排斥能EAB2

(EA+EAB1+EAB2)

1

-

+

5*0*0*0*0-1*0*0*0*0

83519.04

1

-

+

0.9

0.9

1.1

1.1

0.1

0.1

2.1

-

-

-

83519.04

-

-

-

0.9

1.1

0.1

2.1

-

-

-

83519.04

-

-

-

0.9

1.1

0.1

2.1

-

-

-

83519.04

-

-

-

0.9

1.1

0.1

2.1

-

-

-

83519.04

-

-

-

0.9

1.1

0.1

2.1

0.9

1.1

0.1

2.1

-

-

2

0*3*0*0*0-1*0*0*0*0

84491.84

-

-

2

0.9

0.9

0.9

1

1

1

1

0

0

1.9

-

1

1

84491.84

-

1

1

0.9

1

1

2

0

1.9

-

-

-

84491.84

-

-

-

0.9

0

1

0

0

1.9

-

-

-

84491.84

-

-

-

0.9

0

1

0

0

1.9

-

-

-

84491.84

-

-

-

0.9

0

1

0

0

1.9

0.9

0

1

0

0

1.9

-

-

2

0*0*3*0*0-1*0*0*0*0

84492.94

-

-

2

0.9

0.9

1

0.5

0.5

1

0

0

1.4

-

-

-

84492.94

-

-

-

0.9

0

0.5

0

0

1.4

-

1

1

84492.94

-

1

1

0.9

1

0.5

2

0

1.4

-

-

-

84492.94

-

-

-

0.9

0

0.5

0

0

1.4

-

-

-

84492.94

-

-

-

0.9

0

0.5

0

0

1.4

0.9

0

0.5

0

0

1.4

-

-

2

0*0*0*3*0-1*0*0*0*0

84875.54

-

-

2

0.9

0.9

1

0.33

0.3333

1

0

0

1.23

-

-

-

84875.54

-

-

-

0.9

0

0.3333

0

0

1.23

-

-

-

84875.54

-

-

-

0.9

0

0.3333

0

0

1.23

-

1

1

84875.54

-

1

1

0.9

1

0.3333

2

0

1.23

-

-

-

84875.54

-

-

-

0.9

0

0.3333

0

0

1.23

0.9

0

0.3333

0

0

1.23

-

-

2

0*0*0*0*5-1*0*0*0*0

85393.02

-

-

2

0.9

0.9

1

0.25

0.25

1

0

0

1.15

-

-

-

85393.02

-

-

-

0.9

0

0.25

0

0

1.15

-

-

-

85393.02

-

-

-

0.9

0

0.25

0

0

1.15

-

-

-

85393.02

-

-

-

0.9

0

0.25

0

0

1.15

1

-

1

85393.02

1

-

1

0.9

1

0.25

2

0

1.15

0.9

0

0.25

0

0

1.15

-

-

+

1*4*0*0*0-1*0*0*0*0

106522

-

-

+

1

1

1

0.1

0.1

1.1

1

-

-

106522

1

-

-

1

1

0.1

1.1

-

-

-

106522

-

-

-

0

1

0.1

1.1

-

-

-

106522

-

-

-

0

1

0.1

1.1

-

-

-

106522

-

-

-

0

1

0.1

1.1

0

1

0.1

1.1

-

-

+

1*0*0*0*2-1*0*0*0*0

106810

-

-

-

0

1

1

0.1

0.1

1.1

-

-

-

106810

-

-

-

0

1

0.1

1.1

-

-

-

106810

-

-

-

0

1

0.1

1.1

-

-

-

106810

-

1

-

1

1

0.1

1.1

-

1

-

106810

-

-

+

1

1

0.1

1.1

0

1

0.1

1.1

-

-

+

1*0*4*0*0-1*0*0*0*0

106916.2

-

-

+

1

0.5

0.5

0.1

0.1

0.6

-

-

-

106916.2

-

-

-

0

0.5

0.1

0.6

1

-

-

106916.2

1

-

-

1

0.5

0.1

0.6

-

-

-

106916.2

-

-

-

0

0.5

0.1

0.6

-

-

-

106916.2

-

-

-

0

0.5

0.1

0.6

0

0.5

0.1

0.6

-

-

+

1*0*0*2*0-1*0*0*0*0

107392

-

-

-

0

0.5

0.5

0.1

0.1

0.6

-

-

-

107392

-

-

-

0

0.5

0.1

0.6

-

-

-

107392

-

1

-

1

0.5

0.1

0.6

-

1

-

107392

-

-

-

0

0.5

0.1

0.6

-

-

-

107392

-

-

+

1

0.5

0.1

0.6

0

0.5

0.1

0.6

如果等位点A为1，B为0，记为1；A为0，B为1记为2；AB都是1记为“+”；AB都是0记为“-”。

设迭代次数和排斥能成反比，

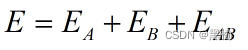
排斥能的计算方法为

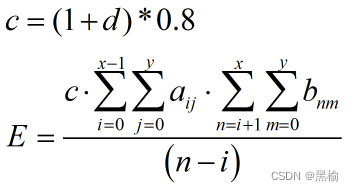
因为A有2个点，B有1个点，且A和B有一个点重合，因此整个差值结构中只有一个1和一个+，在3*5的结构中这两个对象只可能有3种相对位置关系，他们相距为0或者相距1个单位，或者相距2个单位。因此排斥能只可能有3种情况。

0

0

1

0

1

1

>

0

1

因为网络0*3-0*0的迭代次数大于网络2*1-0*0，因此两个1在同一行的排斥能可以估计为0.9.

0

0

1

0

1

2

<

0

2

因为网络0*2-0*1的迭代次数小于网络2*0-0*1，因此1和2在同一行的排斥能估计为1..1.

1

2

已有大量实验表明，对单列的差值结构，如果1和2在同一列这个网络不收敛，因此E为0.

用E的方法不能直接计算+的排斥能，因为两点距离为0，设+的排斥能为x

现在有

-

-

2

0*0*0*0*5-1*0*0*0*0

85393.02

-

-

2

0.9

0.9

1

0.25

0.25

1

0

0

1.15

-

-

-

85393.02

-

-

-

0.9

0

0.25

0

0

1.15

-

-

-

85393.02

-

-

-

0.9

0

0.25

0

0

1.15

-

-

-

85393.02

-

-

-

0.9

0

0.25

0

0

1.15

1

-

1

85393.02

1

-

1

0.9

1

0.25

2

0

1.15

0.9

0

0.25

0

0

1.15

-

-

+

1*4*0*0*0-1*0*0*0*0

106522

-

-

+

1

1

1

x

1+x

1

-

-

106522

1

-

-

1

1

1+x

-

-

-

106522

-

-

-

0

1

1+x

-

-

-

106522

-

-

-

0

1

1+x

-

-

-

106522

-

-

-

0

1

1+x

0

1

1+x

因为设短程相互作用不能隔行传播，因此1*4*0*0*0-1*0*0*0*0只有1组EAB，就是+的排斥能，由此得到

1+x<1.15

因此可以估计x为0.1.

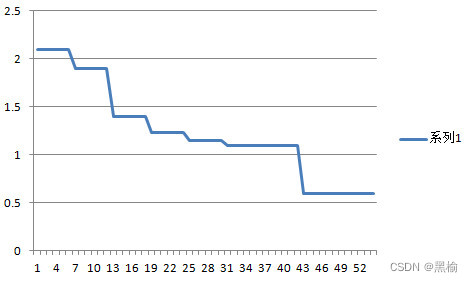
迭代次数和排斥能成反比。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/936030.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

JDK介绍

JDK介绍

JDK,JRE和JVM之间的关系 JVM是运行环境&#xff0c;JRE是含运行环境和相关的类库&#xff0c;跟node环境是一个意思 JDK目录介绍 目录名称说明bin该路径下存放了JDK的各种工具命令。javac和java就放在这个目录。conf该路径下存放了JDK的相关配置文件include该路径下存放了一些…
阅读更多...
DevOps系列文章 之 Python基础

DevOps系列文章 之 Python基础

流程控制和循环 if语句 它由三部分组成: 关键字本身, 用于判断结果真假的条件表达式, 以及当表达式为真或者非零时执行的代码块 可支持else和elif;条件表达式并不需要用括号括起来 1、标准if 条件语句的语法如下&#xff1a; if expression:expr_true_suite 如果表达式的值…
阅读更多...
Java获取环境变量和运行时环境信息和自定义配置信息

Java获取环境变量和运行时环境信息和自定义配置信息

System.getenv() 获取系统环境变量 public static void main1() {Map<String, String> envMap System.getenv();envMap.entrySet().forEach(x-> System.out.println(x.getKey() "" x.getValue())); } System.getenv() 获取的是操作系统环境变量列表&…
阅读更多...
nginx-获取客户端IP地址

nginx-获取客户端IP地址

上有服务器与客户端中间是有nginx代理服务器的&#xff0c;上游服务器如何获取客户端真实ip地址&#xff1f; nginx代理服务器设置X-Forwarded-For的header参数&#xff0c;代理服务器通过remote_addr获取客户端ip地址&#xff0c;将ip地址写入nginx代理服务器的X-Forwarded-Fo…
阅读更多...
激活函数总结（二十一）：激活函数补充(APL、Inverse Cubic)

激活函数总结（二十一）：激活函数补充(APL、Inverse Cubic)

激活函数总结&#xff08;二十一&#xff09;&#xff1a;激活函数补充 1 引言2 激活函数2.1 Adaptive piecewise linear&#xff08;APL&#xff09;激活函数2.2 Inverse Cubic激活函数 3. 总结 1 引言 在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、…
阅读更多...
JS-this知识点、面试题

JS-this知识点、面试题

一、this指向什么 1.简介 2.规则一&#xff1a;默认绑定 3.规则二&#xff1a;隐式绑定 4.规则四&#xff1a;new绑定 5.规则三&#xff1a;显式绑定 call、apply、bind 6.内置函数的绑定 7.规则优先级 8.this规则之外--es6剪头函数 9.ES6剪头函数this 二、This面试题 面试题…
阅读更多...
哔哩哔哩 B站 bilibili 视频视频音效调节 清澈人声

哔哩哔哩 B站 bilibili 视频视频音效调节 清澈人声

视频音效调节方式&#xff1a;直接视频播放内容界面内鼠标右键点击视频音效调节 注意&#xff1a;需要使用的是谷歌浏览器&#xff0c;我的火狐浏览器试了不行&#xff0c;都没选项&#xff0c;火狐的出来的界面是这样的&#xff1a; 目录 具体操作如下&#xff1a; 1、谷歌…
阅读更多...
FreeSWITCH 1.10.10 简单图形化界面3 - 阿里云NAT设置

FreeSWITCH 1.10.10 简单图形化界面3 - 阿里云NAT设置

FreeSWITCH 1.10.10 简单图形化界面3 - 阿里云NAT设置 0、 界面预览1、 查看IP地址2、 修改协议配置3、 开放阿里云安全组4、 设置ACL5、 设置协议中ACL&#xff0c;让PBX匹配内外网6、 重新加载SIP模块7、 查看状态8、 测试一下 0、 界面预览 http://myfs.f3322.net:8020/ 用…
阅读更多...
【数据结构】手撕顺序表

【数据结构】手撕顺序表

一&#xff0c;概念及结构 顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构&#xff0c;一般情况下采用数组存储&#xff1b; 在数组上完成数据的增删查改。 1&#xff0c; 静态顺序表&#xff1a;使用定长数组存储元素。 2.&#xff0c;动态顺序表&#xff1…
阅读更多...
什么是例程，子例程，标签，函数，标签，过程，类方法，静态方法，实例方法，对象方法

什么是例程，子例程，标签，函数，标签，过程，类方法，静态方法，实例方法，对象方法

文章目录 什么是例程&#xff0c;子例程&#xff0c;标签&#xff0c;函数&#xff0c;标签&#xff0c;过程&#xff0c;类方法&#xff0c;静态方法&#xff0c;实例方法&#xff0c;对象方法 编程语言例程 - Routine子例程 - Subroutine函数 - Function标签 - Label过程 - P…
阅读更多...
【C++】详细介绍模版初阶—函数模版、类模板

【C++】详细介绍模版初阶—函数模版、类模板

文章目录 一、泛型编程二、函数模版2.1 函数模版概念2.2 函数模版格式2.3 函数模版的原理2.4 函数模版的实例化2.5 函数模版的匹配原则 三、类模版3.1 类模版定义3.2 类模版实例化 总结 ヾ(๑╹◡╹)&#xff89;" 人总要为过去的懒惰而付出代价ヾ(๑╹◡╹)&#xff89;&…
阅读更多...
【Android Framework系列】第12章 RecycleView相关原理及四级缓存策略分析

【Android Framework系列】第12章 RecycleView相关原理及四级缓存策略分析

1 RecyclerView简介 RecyclerView是一款非常强大的widget&#xff0c;它可以帮助您灵活地显示列表数据。当我开始学习 RecyclerView的时候&#xff0c;我发现对于复杂的列表界面有很多资源可以参考&#xff0c;但是对于简单的列表展现就鲜有可参考的资源了。虽然RecyclerView的…
阅读更多...
《Zookeeper》源码分析（二十三）之 客户端的命令处理过程

《Zookeeper》源码分析（二十三）之 客户端的命令处理过程

目录 客户端的命令处理过程1. ZooKeeper.create()2. ClientCnxn.submitRequest()3. SendThread.run()4. ClientCnxnSocket.doTransport()5. SendThread.readResponse() 客户端的命令处理过程 以创建节点命令为例&#xff0c;整个过程流程如下&#xff1a; CliCommand命令在抽…
阅读更多...
1.Redis 5 环境搭建

1.Redis 5 环境搭建

一、环境搭建 如果是Centos8&#xff0c;yum 仓库中默认的 Redis版本就是5&#xff0c;直接yum install即可。如果是Centos7&#xff0c;yum 仓库中默认的 Redis版本是3系列&#xff0c;比较老~ 为了我们能在 Centos7中下载到 Redis5 首先要安装额外的软件源 sudo yum insta…
阅读更多...
理解HTTPS/TLS/SSL（一）基础概念+配置本地自签名证书

理解HTTPS/TLS/SSL（一）基础概念+配置本地自签名证书

文章目录 没有HTTPS时的样子场景模拟WireShark的Capture Filter和Display Filter设置Capture Filter启动程序设置Display Filter过滤抓到的包 结论 关于为什么加密更简洁有力的回答对称加密和非对称加密和CA证书密钥交换对称加密非对称加密CA机构和证书如何解决客户端和CA机构之…
阅读更多...
centos安装oracle11g

centos安装oracle11g

版本&#xff1a;Oracle 11.2.0.4 创建用户 root执行以下命令 #创建database用户组 groupadd database #创建oracle用户并放入database组中 useradd oracle -g database #设置oracle密码 passwd oracle密码我设置的是database2023 安装oracle安装程序依赖程序包 root用户执…
阅读更多...
在 WSL2 中使用 NVIDIA Docker 进行全栈开发和深度学习 TensorFlow pytorch GPU 加速

在 WSL2 中使用 NVIDIA Docker 进行全栈开发和深度学习 TensorFlow pytorch GPU 加速

WSL2使用NVIDIA Docker进行全栈开发和深度学习 1. 前置条件 1.1. 安装系统 Windows 10 版本 2004 及更高版本&#xff08;内部版本 19041 及更高版本&#xff09;或 Windows 11 跳过 1.2. 处理好网络环境 安装过程中需要访问国际网络&#xff0c;自行处理好。建议开启 tu…
阅读更多...
驾驶员监控系统DMS系统功能规范

驾驶员监控系统DMS系统功能规范

概述 文档范围 该文档阐述了DMS系统的功能场景、系统组成、接口需求等。 目的 该功能规范为DMS系统及周边件的开发提供参考。 缩写与定义 英文缩写 英文全称 中文描述 DMS: Driver Monitoring System 驾驶员监控系统 MPU: Micro Processor Unit 微处理器单元 IECU: …
阅读更多...
windows安装mysql8.0.34的压缩包

windows安装mysql8.0.34的压缩包

文章目录 目录 文章目录 前言 一、下载安装包zip格式 二、使用步骤 总结 前言 一、下载安装包zip格式 MySQL :: Begin Your Download 二、使用步骤 解压缩之后在解压之后的目录里创建data和my.ini my.ini内容 # 设置mysql客户端连接服务端时默认使用的端口 port3306#默认…
阅读更多...
＜C++＞ STL_list

＜C++＞ STL_list

1.list的介绍 list是可以在常数范围内在任意位置进行插入和删除的序列式容器&#xff0c;并且该容器可以前后双向迭代。list的底层是双向链表结构&#xff0c;双向链表中每个元素存储在互不相关的独立节点中&#xff0c;在节点中通过指针指向 其前一个元素和后一个元素。list与…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023