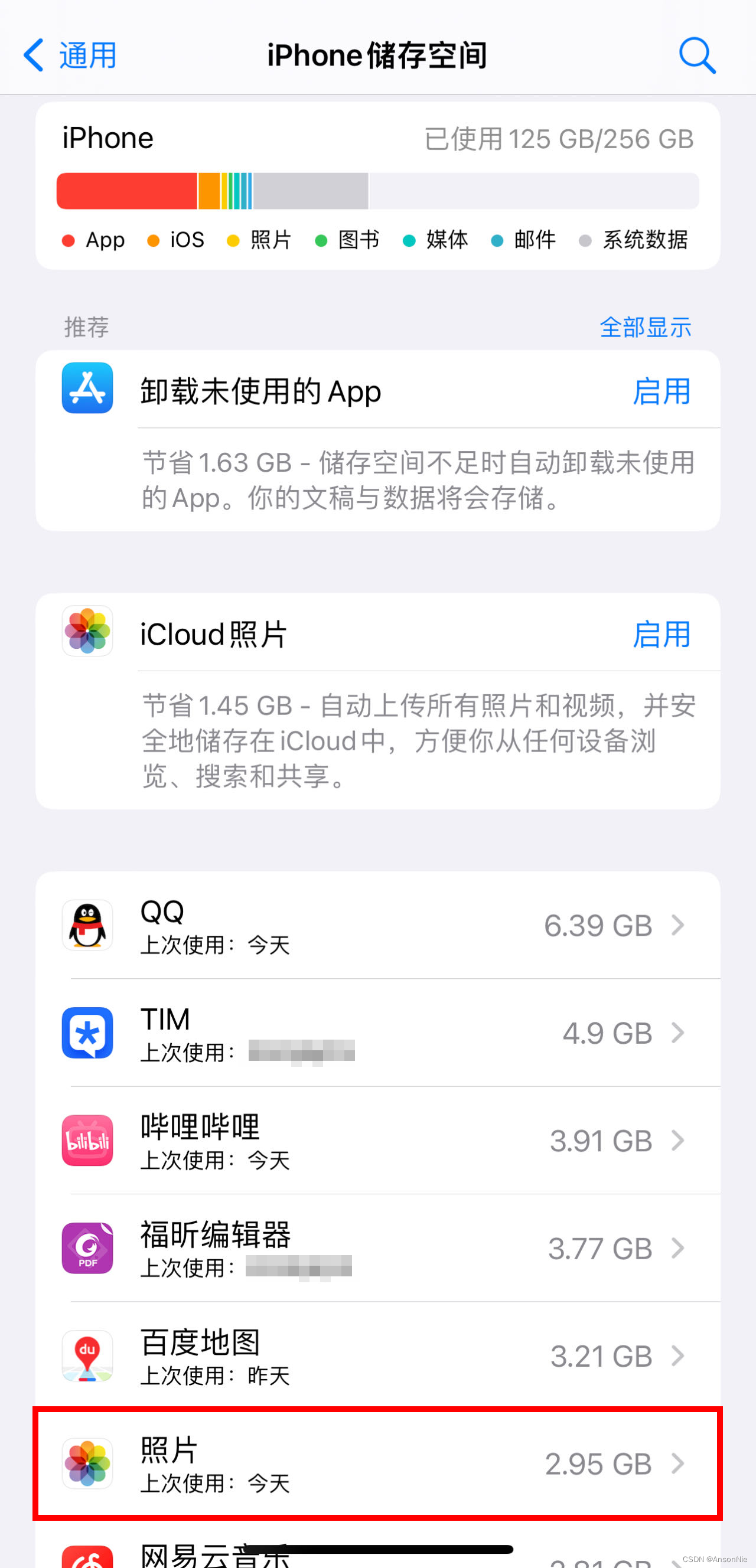
nonlocal关键字声明

news2024/9/25 9:35:23

nonlocal关键字声明

作用

使得内层函数可以使用/修改外层函数的变量

值得注意的是，在未使用nonlocal声明时

对于外层函数中的可变对象，内层函数即可访问，也可以修改

def outer():
    x, y = [1], [2]

    def inner(z):
        x.append(1)
        print(x)
        print(z)

    return inner


outer()([3])

[1, 1]
[3]

对于外层函数中的不可变对象，如数字、字符串，只能访问，不能修改
```
def outer():
    x, y = 1, 2

    def inner(z):
        print(x)
        x += 1
        print(x)
        print(z)

    return inner


outer()(3)
```
```
UnboundLocalError: local variable 'x' referenced before assignment
```
可以发现：

两个print(x)均未被执行

即，只要在内部函数中尝试修改外部函数中的不可变变量，那么在调用内部函数时，就会直接报错，而不是一句一句执行，直到遇到错误的那行代码

使用nonlocal声明时

def outer():
    x, y = 1, 2

    def inner(z):
        nonlocal x
        x += 1
        print(x)
        print(z)

    return inner


outer()(3)

2
3

应用场景

如果外层函数中的变量被内层函数使用，并且内层函数是外层函数的返回值，就会形成闭包，有以下特点：

被内层函数使用的外层函数变量，在外层函数调用完毕后不会被销毁，而是与内层函数共同组成闭包，隐藏在闭包里面，这里姑且称为外层残余变量
只有通过调用作为外层函数返回值的内层函数才能访问/修改这些被封存在闭包里面的外层残余变量，这是唯一途径，也是”闭“的含义
- 如果外层残余变量为不可变对象，那么可以通过nonlocal关键字声明进行修改
- 如果外层残余变量为可变对象，那么可以直接进行修改
闭包可以看作一个分多步调用的函数
1. 首先调用外层函数
2. 然后调用返回的内层函数

stable baselines3是一个深度强化学习算法库，提供以下方法供用户自定义学习率更新策略，链接

链接的意思就是，所有算法都支持传入一个以固定参数progress_remaining为输入的闭包函数作为学习率更新策略，随训练进程，progress_remaining自动从 $1\rightarrow 0$ ，RL Zoo 里面实现了一个线性衰减的学习率更新策略，示例如下：

from typing import Callable

from stable_baselines3 import PPO


def linear_schedule(initial_value: float) -> Callable[[float], float]:
    """
    Linear learning rate schedule.

    :param initial_value: Initial learning rate.
    :return: schedule that computes
      current learning rate depending on remaining progress
    """
    def func(progress_remaining: float) -> float:
        """
        Progress will decrease from 1 (beginning) to 0.

        :param progress_remaining:
        :return: current learning rate
        """
        return progress_remaining * initial_value

    return func

# Initial learning rate of 0.001
model = PPO("MlpPolicy", "CartPole-v1", learning_rate=linear_schedule(0.001), verbose=1)
model.learn(total_timesteps=20_000)

下面，我们使用nonlocal关键字实现一个更加复杂的多步衰减学习率策略，即指定初始学习率、衰减次数、衰减率，随训练进程在特定步数自动乘以衰减因子衰减lr

import numpy as np
from matplotlib import pyplot as plt


def multi_step_decay_schedule(init_value, decay_times=9, gamma=0.7):
    lr = init_value
    progress_nodes = np.linspace(1 - 1 / (1 + decay_times), 0, decay_times, endpoint=False)
    progress_mask = np.full(decay_times, True, dtype=bool)

    def func(progross_remaining):
        # lr是float不可变对象，需要更新lr作为返回值，因此用nonlocal声明
        # progress_mask、progress_nodes为可变对象，无需nonlocal声明
        nonlocal lr
        for i in range(decay_times):
            if progress_mask[i] and abs(progress_nodes[i] - progross_remaining) < 1e-3:
                progress_mask[i] = False
                # 将学习率乘以gamma
                lr = lr * gamma
        return lr

    return func


if __name__ == "__main__":
    lr_schedule = multi_step_decay_schedule(0.1)
    progross_remaining = np.arange(1, 0, -0.001)
    lr = [lr_schedule(p) for p in progross_remaining]
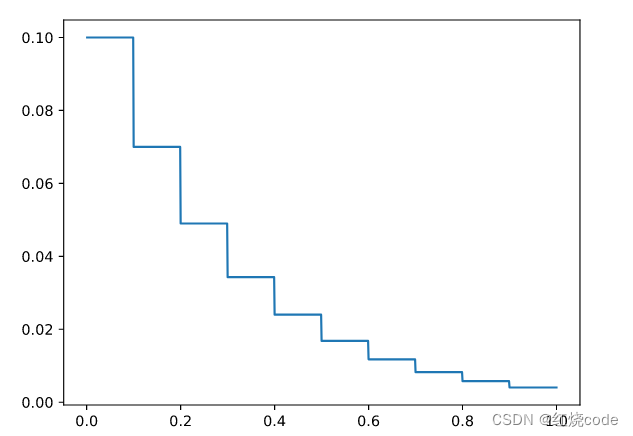
    plt.plot(progross_remaining[::-1], lr)
    plt.show()