---

引言

承接前文，在对运输问题有了基本的了解后，我们开始深入学习表上作业的具体内容。

---

二、表上作业法

2.1 初始基可行解的确定

2.1.1 最小元素法

基本思想：应优先考虑单位运价最小（或运距最短）的供销业务，最大限度地满足其供销量。然后，在余下的供、销点的供销关系中继续按照上述方法安排调运，直至安排所有供销任务，得到一个完整的调运方案为止。这样就得到了一个初始基可行解。

2.1.2 伏格尔法

初看起来，最小元素法十分合理。但是，有时按照最小单位运价优先安排物品调运时，却可能导致不得不采取运费很高的供销点对，从而使整个运输费用增加。对每一个产地或销地，均可由它到销地或产地的单位运价中找到最小单位运价和次小单位运价，并称这两个单位运价之差为该产地或销地的罚数。

若罚数的值不大，当不能按照最小单位运价安排运输时造成的运费损失不大；反之，如果罚数的值很大，不按最小运价组织运输就会造成很大损失，故应尽量按照最小单位运价来运输。

基本思想：首先计算运输表中每一行和每一列的次小单位运价和最小单位运价之间的差值，并分别称为行罚数和列罚数。将算出的行罚数填入位于运输表右侧行罚数栏的左边第一列的相应格子中，列罚数填入位于运输表下边列罚数栏的第一行的相应格子中。

在这些罚数中，确定最大者，对应的运输格优先填入尽可能大的运量（同列或同行中优先满足运价小的），同最小元素法一样，去掉相应的行或列，表示已经满足需求了。在尚未去掉的各行各列中如上重新计算各行各列罚数，重复操作，最终得到一个基本可行解。

以下表为例，格内右上角的小小格表示对应的单位运费。

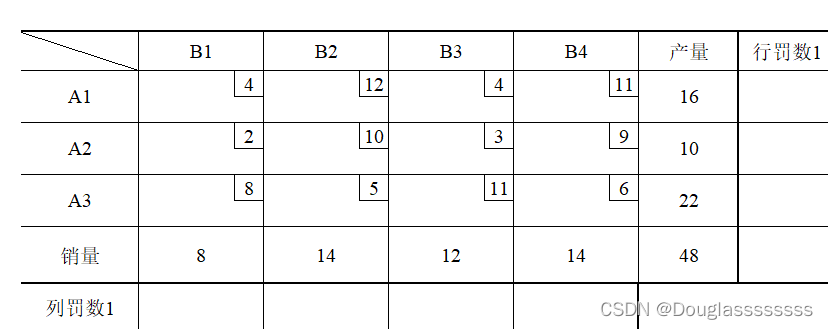
对于产地 A1 ，其运往销地最小单位运费为 4 ，次小单位运费也为 4 ，两者之差为 0 ，故其行罚数1 为 0 ；对于销地 B1 ，各个产地运往最小单位运费为 2 ，次小为 4，两者之差为 2 ，故其列罚数1 为 2 ，同理，可将各个产地和销地的罚数计算出来。

得到罚数最大的为 B2 的列罚数 5 ，故优先满足 B2 的销量。其中 A3 运往 B2 的单位运价最小，故先填写 A3-B2 格。由于 A3 产量为 22，故可直接满足 B2，在 A3-B2 格填入 14，同时划去 B2 列。并可重新计算各行各列罚数，如下表所示。

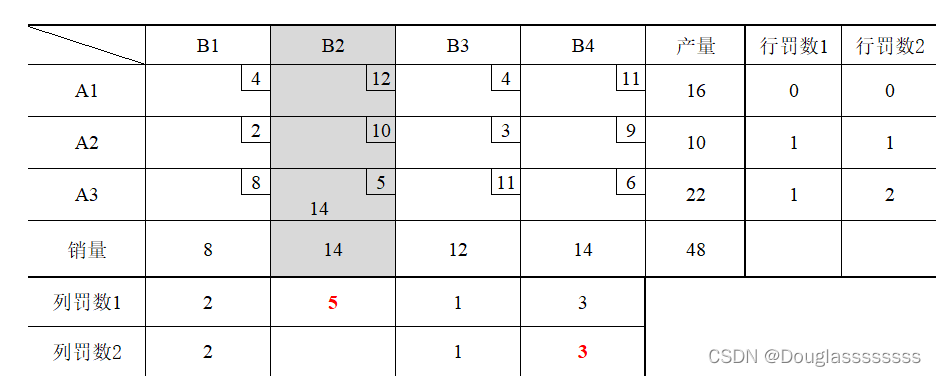
往后可同理得出其他运量，最终的运输表如下：

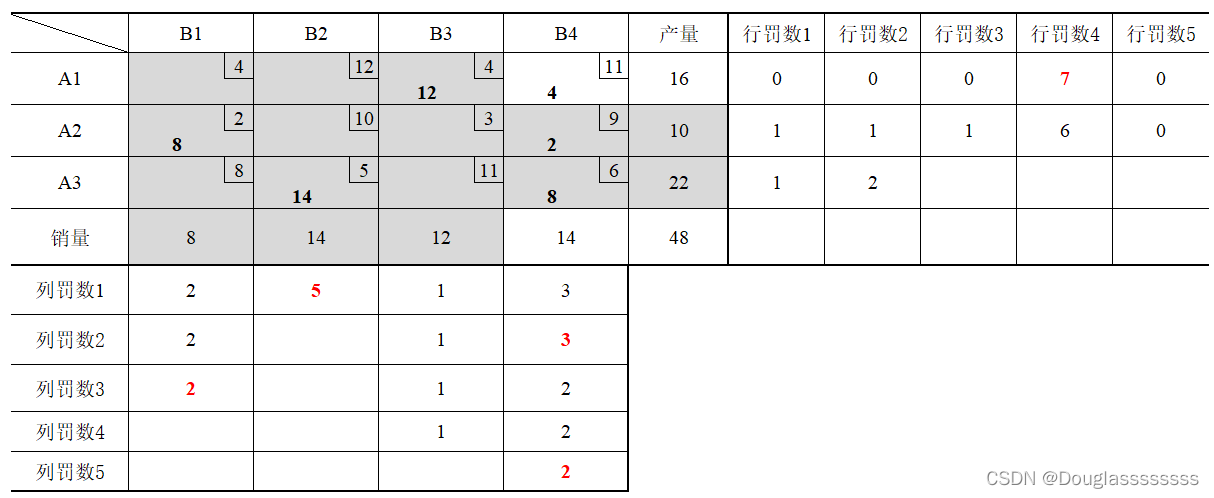
中间又出现罚数相同的情况，两个都可以选，所以最终结果可能有些不同，不过没关系，只是得出一个初始解，后面还需要检验和调整的。

本例得出的初始解目标函数值为 $z=2\times 8+14\times 5+12\times 4+4\times 11+2\times 9+8\times 6=244.$

一般来说，伏格尔法得出的初始解质量最好，常用来作为运输问题最优解的近似解。

---

写在最后

求出初始解后，需要对其进行检验和改正，我们放到后面来细说。