词嵌入
词嵌入(Word Embedding)是自然语言处理(NLP)中的一种技术,用于将文本中的单词映射到一个低维向量空间中。它是将文本中的单词表示为实数值向量的一种方式。
在传统的文本处理中,通常使用独热编码(One-Hot Encoding)来表示单词,即将每个单词表示为一个稀疏的高维向量,向量中只有一个位置为1,其余位置为0。这种表示方式无法捕捉到单词之间的语义关系和相似性。
而词嵌入通过将单词映射到一个连续的向量空间中,使得具有相似语义的单词在向量空间中的距离更近。这样的表示方式可以更好地表达单词之间的语义关系,并且可以用于计算单词的相似度、聚类、分类等任务。
词嵌入模型通常是通过无监督学习的方式从大规模的文本语料库中学习得到的。一种常用的词嵌入模型是Word2Vec,它使用了神经网络模型来训练词嵌入向量。其他常见的词嵌入模型还包括GloVe、FastText等。
使用预训练的词嵌入模型,可以将文本中的单词转换为对应的词嵌入向量,从而为文本数据提供更丰富的表示。这对于各种NLP任务,如文本分类、命名实体识别、情感分析等,都具有重要的作用,并且可以提升模型的性能和效果。
文章内容来自李沐大神的《动手学深度学习》并加以我的理解,感兴趣可以去https://zh-v2.d2l.ai/查看完整书籍
文章目录
- 词嵌入
- 为什么独热向量是一个糟糕的选择
- 自监督的word2vec
- 跳元模型(Skip-Gram)
- 定义
- 训练
- 连续词袋(CBOW)模型
- 定义
- 训练
为什么独热向量是一个糟糕的选择
-
维度灾难
独热向量需要为每个可能的取值创建一个维度,这样会导致数据集在高维空间中变得非常稀疏。对于具有大量类别或取值的特征,独热编码会导致高维度的输入空间,这会增加模型的复杂性和计算开销。 -
信息损失
独热向量将每个取值都视为独立的特征,忽略了它们之间的相关性。这可能会导致丢失一些重要的信息。
我们一般使用余弦相似度来描述两个向量之间的相关性:
x T y ∣ ∣ x ∣ ∣ ∣ ∣ y ∣ ∣ ∈ [ − 1 , 1 ] \frac{x^Ty}{||x||||y||}\in [-1,1] ∣∣x∣∣∣∣y∣∣xTy∈[−1,1]
若我们使用独热编码,任意两个向量之间的余弦相似度为0. -
统计效率低:独热向量会引入大量的零值,这对于统计建模来说可能是低效的。在数据集中存在大量零值的情况下,计算和存储这些稀疏向量的开销将会增加。
-
增加模型复杂性:独热向量会引入大量的特征维度,这可能导致模型的复杂性增加。对于某些机器学习算法,如决策树和神经网络,高维度的输入空间可能会导致模型过拟合的问题。
自监督的word2vec
为了解决独热编码的问题,我们引入word2vec方法。
Word2Vec 是一种用于将词汇映射到连续向量空间的技术,它是由 Google 在 2013 年开发的一种词嵌入(Word Embedding)方法。Word2Vec 通过学习大规模文本语料库中的上下文信息,将每个单词表示为一个稠密的向量,以便在计算机中更好地处理和理解自然语言。
Word2Vec 有两种主要的模型架构:连续词袋模型(Continuous Bag of Words, CBOW)和跳字模型(Skip-gram)。这两种模型都基于相同的原理:根据上下文单词的共现关系来学习词向量。
-
连续词袋模型(CBOW):CBOW 模型的目标是根据上下文单词来预测目标单词。它将上下文中的单词作为输入,通过一个浅层神经网络模型来学习目标单词的向量表示。
-
跳字模型(Skip-gram):Skip-gram 模型与 CBOW 模型相反,它的目标是根据目标单词来预测上下文单词。它通过训练来学习目标单词和上下文单词之间的关系,以得到每个单词的向量表示。
Word2Vec 使用的核心思想是“共现性”,即假设在语料库中,经常在相似的上下文中出现的单词也具有相似的语义含义。通过学习这种共现关系,Word2Vec 可以生成具有语义信息的词向量。这些词向量可以用于各种自然语言处理任务,如文本分类、命名实体识别、机器翻译等。
Word2Vec 的优点包括:
- 将离散的词汇表示为连续向量,使得单词更容易用数学方式进行处理和计算。
- 通过捕捉上下文关系,生成的词向量可以表达单词的语义和语法信息。
- 可以从大规模的未标记文本数据中自动学习词向量,无需人工标注数据。
- 生成的词向量可以在各种自然语言处理任务中作为特征输入,提高模型的性能。
需要注意的是,Word2Vec 也有一些限制和注意事项,例如对于罕见的单词可能无法得到很好的向量表示,以及在处理多义词时可能存在一定的歧义。此外,对于特定任务,可能需要对生成的词向量进行进一步微调或调整。
总体而言,Word2Vec 是一种非常有用且广泛应用的词嵌入技术,对于许多自然语言处理应用具有重要作用。
跳元模型(Skip-Gram)
定义
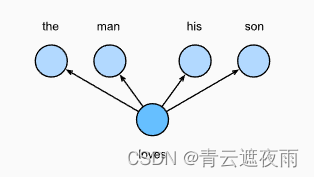
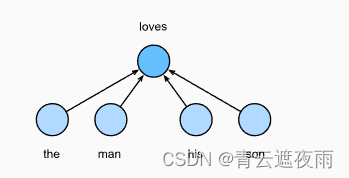
简单来说,跳元模型就是通过假设一个词可以用来在文本序列中生成其周围的单词。以文本序列“the”“man”“loves”“his”“son”为例。假设中心词选择“loves”,并将上下文窗口设置为2,如图所示,给定中心词“loves”,跳元模型考虑生成上下文词“the”“man”“him”“son”的条件概率:
P
(
"
t
h
e
"
,
"
m
a
n
"
,
"
h
i
s
"
,
"
s
o
n
"
∣
"
l
o
v
e
"
)
P("the","man","his","son"|"love")
P("the","man","his","son"∣"love")
若假设上下文词是在给定中心词的情况下独立生成的(即条件独立性)。在这种情况下,上述条件概率可以重写为:
P
(
"
t
h
e
"
∣
"
l
o
v
e
"
)
⋅
P
(
"
m
a
n
"
∣
"
l
o
v
e
"
)
⋅
P
(
"
h
i
s
"
∣
"
l
o
v
e
"
)
⋅
P
(
"
s
o
n
"
∣
"
l
o
v
e
"
)
P("the"|"love")\cdot P("man"|"love")\cdot P("his"|"love")\cdot P("son"|"love")
P("the"∣"love")⋅P("man"∣"love")⋅P("his"∣"love")⋅P("son"∣"love")
在跳元模型中,每个词都有两个
d
d
d维向量表示,用于计算条件概率。更具体地说,对于词典中索引为
i
i
i的任何词,分别用
v
i
∈
R
d
v_i\in R^d
vi∈Rd和
u
i
∈
R
d
u_i\in R^d
ui∈Rd表示其用作中心词和上下文词时的两个向量。给定中心词
w
c
w_c
wc(词典中的索引
c
c
c),生成任何上下文词
w
o
w_o
wo(词典中的索引
o
o
o)的条件概率可以通过对向量点积的softmax操作来建模:
P
(
w
o
∣
w
c
)
=
e
x
p
(
u
o
T
v
c
)
∑
i
∈
V
e
x
p
(
u
i
T
v
c
)
P(w_o|w_c)=\frac{exp(u_o^Tv_c)}{\sum_{i\in V}exp(u_i^Tv_c)}
P(wo∣wc)=∑i∈Vexp(uiTvc)exp(uoTvc)
其中词表索引集
V
=
0
,
1
,
.
.
.
,
∣
V
∣
−
1
V={0,1,...,|V|-1}
V=0,1,...,∣V∣−1,给定长度为
T
T
T的文本序列,其中时间步
t
t
t处的词表示为
w
t
w^{t}
wt。假设上下文词是在给定任何中心词的情况下独立生成的。对于上下文窗口
m
m
m,跳元模型的似然函数是在给定任何中心词的情况下生成所有上下文词的概率:
∏
t
=
1
T
∏
−
m
≤
j
≤
m
,
j
≠
0
P
(
w
t
+
j
∣
w
t
)
\prod_{t=1}^{T} \prod_{-m\leq j \leq m,j\neq0}P(w^{t+j}|w^{t})
t=1∏T−m≤j≤m,j=0∏P(wt+j∣wt)
其中可以省略小于
1
1
1或大于
t
t
t的任何时间步。
训练
跳元模型参数是词表中每个词的中心词向量和上下文词向量。在训练中,我们通过最大化似然函数(即极大似然估计)来学习模型参数。这相当于最小化以下损失函数:
−
∑
t
=
1
T
∑
−
m
≤
j
≤
m
,
j
≠
0
l
o
g
P
(
w
(
t
+
j
)
∣
w
(
t
)
)
-\sum_{t=1}^{T}\sum_{-m\leq j \leq m,j\neq0}logP(w^{(t+j)}|w^{(t)})
−t=1∑T−m≤j≤m,j=0∑logP(w(t+j)∣w(t))
当使用随机梯度下降来最小化损失时,在每次迭代中可以随机抽样一个较短的子序列来计算该子序列的(随机)梯度,以更新模型参数。为了计算该(随机)梯度,我们需要获得对数条件概率关于中心词向量和上下文词向量的梯度。通常,涉及中心词
w
c
w_c
wc和上下文词
w
o
w_o
wo的对数条件概率为:
l
o
g
P
(
w
o
∣
w
c
)
=
u
o
T
v
c
−
l
o
g
(
∑
i
∈
V
e
x
p
(
u
i
T
v
c
)
)
logP(w_o|w_c)=u_o^Tv_c-log(\sum_{i\in V}exp(u_i^Tv_c))
logP(wo∣wc)=uoTvc−log(i∈V∑exp(uiTvc))
通过微分,我们可以获得其相对于中心词向量
v
c
v_c
vc的梯度为
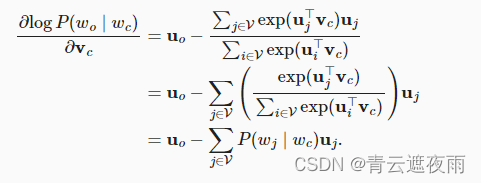
注意, 上式中的计算需要词典中以
w
c
w_c
wc为中心词的所有词的条件概率。其他词向量的梯度可以以相同的方式获得。
对词典中索引为
i
i
i的词进行训练后,得到
v
i
v_i
vi(作为中心词)和
u
i
u_i
ui(作为上下文词)两个词向量。在自然语言处理应用中,跳元模型的中心词向量通常用作词表示。
对于如何具体使用和训练跳元模型,我将在后面的博客中给出
连续词袋(CBOW)模型
定义
连续词袋(CBOW)模型类似于跳元模型。与跳元模型的主要区别在于,连续词袋模型假设中心词是基于其在文本序列中的周围上下文词生成的。例如,在文本序列“the”“man”“loves”“his”“son”中,在“loves”为中心词且上下文窗口为2的情况下,连续词袋模型考虑基于上下文词“the”“man”“him”“son”(如下图所示)生成中心词“loves”的条件概率,即:
P
(
"
l
o
v
e
"
∣
"
t
h
e
"
,
"
m
a
n
"
,
"
h
i
s
"
,
"
s
o
n
"
)
P("love"|"the","man","his","son")
P("love"∣"the","man","his","son")
由于连续词袋模型中存在多个上下文词,因此在计算条件概率时对这些上下文词向量进行平均。具体地说,对于字典中索引
i
i
i的任意词,分别用
v
i
∈
R
d
v_i\in R^d
vi∈Rd和
u
i
∈
R
d
u_i\in R^d
ui∈Rd表示用作上下文词和中心词的两个向量(符号与跳元模型中相反)。给定上下文词
w
o
1
,
.
.
.
,
w
o
2
m
w_{o1},...,w_{o2m}
wo1,...,wo2m(在词表中索引是
o
1
,
.
.
.
,
o
2
m
o1,...,o2m
o1,...,o2m)生成任意中心词
w
c
w_c
wc(在词表中索引是
c
c
c)的条件概率可以由以下公式建模:
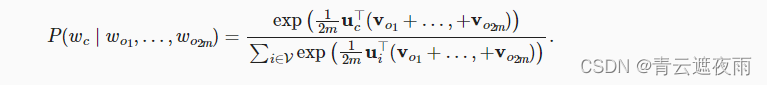
为了简洁起见,我们设为
W
o
=
o
1
,
.
.
,
o
2
m
W_o={o1,..,o2m}
Wo=o1,..,o2m和
v
ˉ
=
(
v
o
1
+
v
o
2
+
.
.
.
+
v
o
2
m
)
/
(
2
m
)
\bar{v}=(v_o1+v_o2+...+v_{o2m})/(2m)
vˉ=(vo1+vo2+...+vo2m)/(2m),那么上述式子可以化简为:
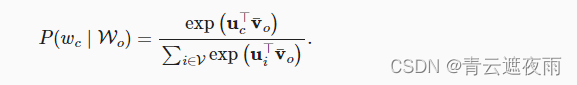
给定长度为
T
T
T的文本序列,其中时间步
t
t
t处的词表示为
w
t
w^{t}
wt。对于上下文窗口
m
m
m,连续词袋模型的似然函数是在给定其上下文词的情况下生成所有中心词的概率:
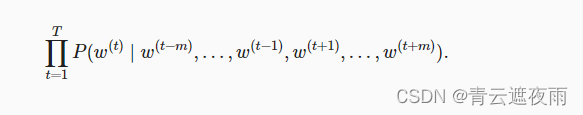
训练
训练连续词袋模型与训练跳元模型几乎是一样的。连续词袋模型的最大似然估计等价于最小化以下损失函数:
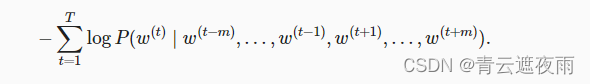
请注意,
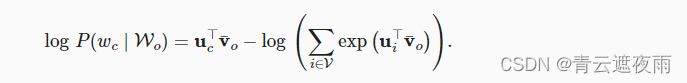
通过微分,我们可以获得其关于任意上下文词向量
v
o
i
v_{oi}
voi(
i
=
1
,
2
,
.
.
.
,
2
m
i=1,2,...,2m
i=1,2,...,2m)的梯度,如下:
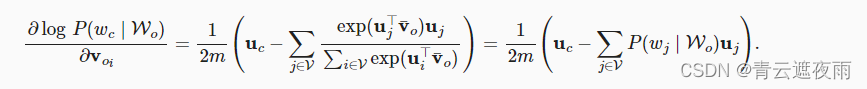
其他词向量的梯度可以以相同的方式获得。与跳元模型不同,连续词袋模型通常使用上下文词向量作为词表示。