一.题目描述

长度最小的子数组

 二.思路分析

题目要求：找出长度最小的符合要求的连续子数组，这个要求就是子数组的元素之和大于等于target。

如何确定一个连续的子数组？确定它的左右边界即可。如此一来，我们最先想到的就是暴力枚举，枚举所有的子数组，找到符合要求的，比较出长度最短的那一个。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int n = nums.size();
        int ret = INT_MAX;
        for (int left = 0; left < n; left++)
        {
            int sum = 0;
            for (int right = left; right < n; right++)
            {
                sum += nums[right];
                if (sum >= target)
                {
                    ret = min(ret, right - left + 1);
                }
            }
        }
        return ret == INT_MAX ? 0 : ret;
    }
};

两层for循环，时间复杂度O(n^2)，leetcode上运行超时，我们需要想办法优化时间复杂度。

时间复杂度这么高就是因为做了大量的枚举，我们是否有办法减少一些不必要的枚举呢？

key1

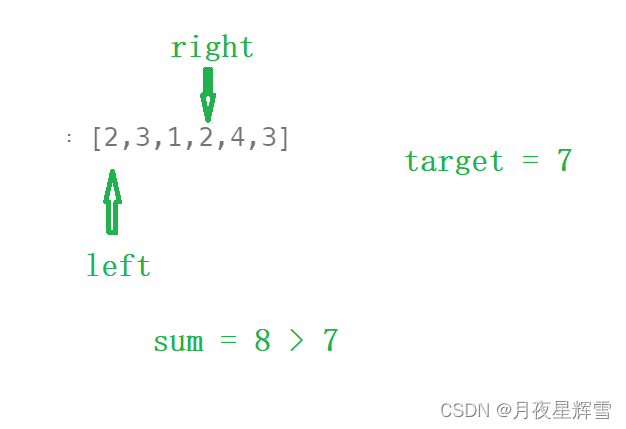
以这个测试用例为例，当right从left位置一直向右移动到该位置，区间之和满足要求，记录此时的长度4并更新结果。

按照暴力枚举的策略right还要继续向后移动。但我们知道，后面的区间肯定也是满足条件的，因为所有的数都是正整数，sum只会越加越大。

即便如此，区间长度肯定也会更大，所以此时就是left固定在第一个位置的局部最优解，right不必再向后枚举了。

key2

left向右移动一个单位，按照暴力枚举策略，right要从图中的标记处回退到left位置 

但我们知道right最终还是会一直往前走，到达原先的标记处。为啥呢？通过上一轮枚举结果，我们已知[left - 1 , tmp)区间是不满足要求的，更别说现在还少了一个数。

所以right没有必要退回去，因为退了也是白退。

key3

所以left前进即可，right不用后退。怎么计算此时区间长度和呢？遍历一遍区间吗？那right岂不是还要回去？其实只需要在left移动之前用sum减去left指向的值即可，然后再移动left。

按照图中的实例，此时不满足条件，所以right继续向后移动，又回到了之前的逻辑。

如果此时满足条件呢？那么这个就是left固定在这个位置的局部最优解了，更新结果之后，left继续向右移动。

故left可能会向后移动多步，所以要用循环实现。

三.代码实现

在代码实现过程中，我们需要用到两个指针（下标）来标记左边界和右边界。通过分析，left和right只会向前移动而不会后退，就像一个窗口一样从左到右划过数组故形象的将这类方法称为滑动窗口，也叫同向双指针。当研究对象是一个连续区间时，并且证明left和right都不用后退时便可以考虑使用滑动窗口解题。

 滑动窗口类题目常见就这几个步骤，先定义两个指针，然后right指向的元素进窗口，判断条件，决定是否出窗口，有时可能需要出多个元素，所以此处可能是一个循环过程，例如本题就是。至于更新结果要根据具体的题目来确定位置，有可能是进窗口以后，又有可能是出窗口之前，还可能是出窗口之后。

整个过程是循环的，当right越界时也就结束了。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int n = nums.size();
        int left = 0, right = 0;
        int sum = 0;
        int ret = INT_MAX;

        while (right < n)
        {
            //进窗口
            sum += nums[right];
           
            //判断
            while (sum >= target)
            {
                //更新结果
                ret = min(ret, right - left + 1);
                //出窗口
                sum -= nums[left++];
            }
            ++right;
        }

        return ret == INT_MAX ? 0 : ret;
    }
};

 最坏的情况就是right和left都走到了末尾，相当于两个指针都遍历一遍数组，时间复杂度为O(n)