https://codeforces.com/contest/1619/problem/E 

翻译：

Dmitry有一个𝑛非负整数数组𝑎1，𝑎2，…，𝑎𝑛。

在一次操作中，Dmitry可以选择任意索引𝑗(1≤𝑗≤𝑛)，并将元素𝑎𝑗的值增加1。他可以多次选择相同的索引𝑗。

对于从0到𝑛的每个𝑖，确定Dmitry是否可以使数组的MEX恰好等于𝑖。如果可能，那么确定最少的操作数。

数组的MEX等于数组中不存在的最小非负整数。例如，数组[3,1,0]的MEX值为2，数组[3,3,1,4]的MEX值为0。

输入
输入数据的第一行包含一个整数𝑡(1≤𝑡≤104)——输入中的测试用例的数量。

下面是测试用例的描述。

每个测试用例描述的第一行包含一个整数𝑛(1≤𝑛≤2⋅105)——数组𝑎的长度。

每个测试用例描述的第二行包含𝑛整数𝑎1，𝑎2，…，𝑎𝑛(0≤𝑎𝑖≤𝑛)-数组𝑎的元素。

可以保证测试中所有测试用例𝑛的值之和不超过2⋅105。

输出
对于每个测试用例，输出𝑛+1整数-𝑖-th number等于可以使数组MEX等于𝑖(0≤𝑖≤𝑛)的最小操作次数，如果不能这样做，则为-1。

例子
inputCopy
5
3.
0 1 3
7
0 1 2 3 4 3 2
4
3 0 0 0
7
4 6 2 3 5 0 5
5
4 0 1 0 4
outputCopy
1 10 10 -1
1 1 2 2 1 0 2 6
3 0 1 4 3
1 0 -1 -1 -1 -1 -1 -1 -1 -1
2 1 0 2 -1 -1
请注意
在第一组示例输入中，𝑛=3:

要得到MEX=0，执行一次增量就足够了:𝑎1++;
要得到MEX=1，执行一次增量就足够了:𝑎2++;
对于给定的数组，MEX=2，因此不需要执行增量;
通过执行增量不可能得到MEX=3。

思路：

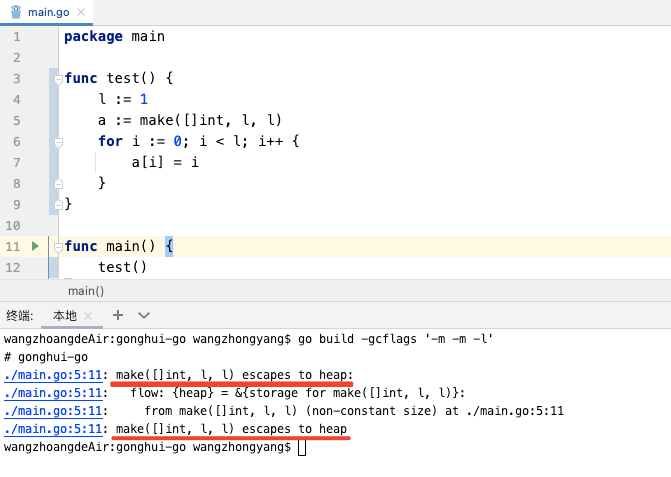
MEX，我们很容易得到一个结论，如果前边比较小的数构不成的时候，那么后边都构不成，因为是未出现的i最小的非负整数，所以我们一旦有一个-1，那么后边就全是-1啦。

然后我们来分析一下，构成的条件是什么，比如说 5，那么它的前边至少要有一个0 1 2 3 4，4的构成条件是0 1 2 3，同理我们可以这样子往前推，直接到0，0的构成条件，只要没有0就好了对吧，所以0的花费就是0出现的个数，那么1呢，如果0不能构成那么1就直接是-1，所以我们直接讨论在前边可以构成的前提下，来构成现在的条件。

1的话，我们的花费也就是1的个数（因为已经在0被构成的前提下），接下来看2，2的话就是在有0 1的情况下加上2的个数，但是我们可能会有没有1 有两个0 的情况，那么我们就需要将一个0 变成1，然后加上2的个数，如果有一个0呢，那么我们就可以直接-1了。

同理，构成三需要2，如果比其小的是0 0 0，那么我们就需要将其变成 0 1 2，对吧，然后花费成本+3的个数，变成0 1 2，如果是3个0的时候，在前边2的情况下，我们就已经将其变成了 0 1 0，所以我们每次只需要在其成本上累加。有可能比其小的数不是0，我们需要将其变大，最小成本就是最大的数去变化，所以我们这里用优先队列优化，也可以用栈，因为我们从小到大，后进入的肯定是最大的，已经变化过的就要固定了，不能再变化pop掉，这思路就很清晰了。

嗲吗：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}

int a[200005];
int w;
void solv(){
    cin>>n;
    map<int,ll>q;
    for (int i =1; i<=n; i++) {
        cin>>w;
        q[w]++;
    }
    bool flag=false;
    ll bl=0;
    priority_queue<int>ff;
    for (int i =0; i<=n; i++) {
        if (flag) {
            printf("-1 ");
        }
        else
        {
            printf("%lld ",bl+q[i]);
        }
        for (int j =0; j<q[i]; j++) {
            ff.push(i);
        }
        if (ff.empty()) {
            flag=true;
        }
        else{
            bl+=i-ff.top();
            ff.pop();
        }
    }
    printf("\n");
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    while (t--) {
        solv();
    }
    return 0;
}