省略的技巧

已知 $f(n)$ 来说，求 $g(n)$

• 表达式中相乘的常量，可以省略，如
  • $f(n)=100\ast n^2$ 中的 $100$
• 多项式中数量规模更小（低次项）的表达式，如
  • $f(n)=n^2+n$ 中的 $n$
  • $f(n)=n^3+n^2$ 中的 $n^2$
• 不同底数的对数，渐进上界可以用一个对数函数 $\log n$ 表示
  • 例如：$lo{g}_2(n)$ 可以替换为 $lo{g}_{10}(n)$，因为 $lo{g}_2(n)=\frac{lo{g}_{10}(n)}{lo{g}_{10}(2)}$，相乘的常量 $\frac{1}{lo{g}_{10}(2)}$ 可以省略
• 类似的，对数的常数次幂可省略
  • 如：$log(n^c)=c\ast log(n)$

常见大 $O$ 表示法

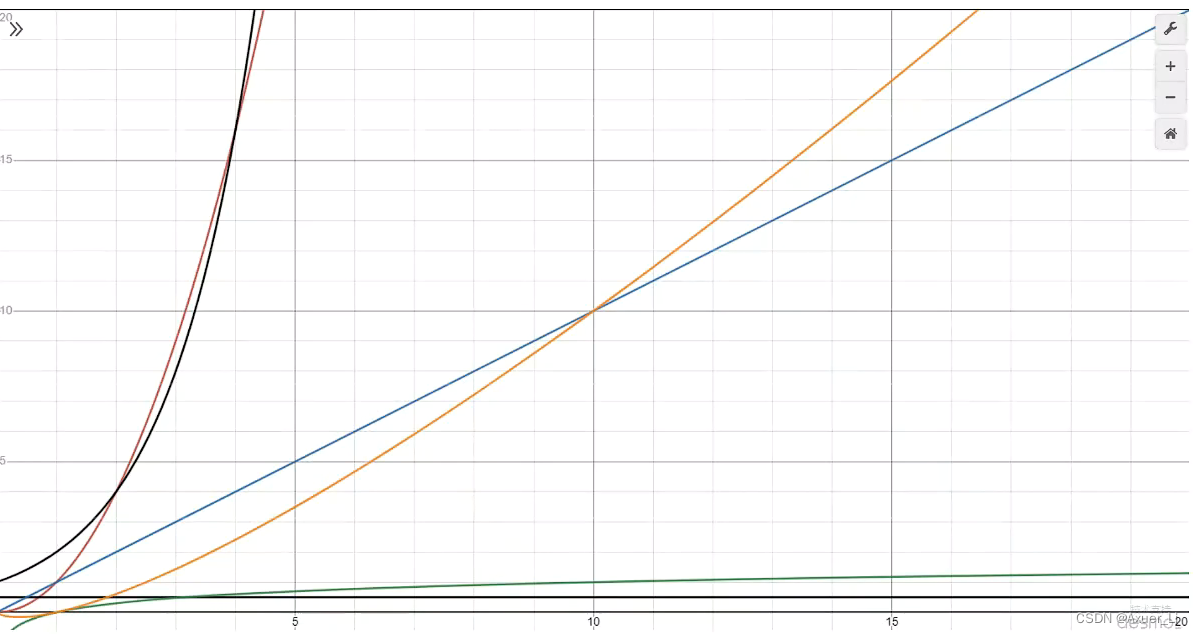
按时间复杂度从低到高

• 黑色横线 $O(1)$，常量时间，意味着算法时间并不随数据规模而变化
• 绿色 $O(log(n))$，对数时间
• 蓝色 $O(n)$，线性时间，算法时间与数据规模成正比
• 橙色 $O(n\ast log(n))$，拟线性时间
• 红色 $O(n^2)$ 平方时间
• 黑色朝上 $O(2^n)$ 指数时间
• 没画出来的 $O(n!)$

空间复杂度

与时间复杂度类似，一般也使用大 $O$ 表示法来衡量：一个算法执行随数据规模增大，而增长的额外空间成本

一个方法中，看新建的对象占用空间有多少