论文地址: 论文
代码地址: 代码
这是一篇效果极好的像素级跟踪的文章, 发表在ICCV2023, 可以非常好的应对遮挡等情形, 其根本的方法在于将2D点投影到一个伪3D(quasi-3D)空间, 然后再映射回去, 就可以在其他帧中得到稳定跟踪.
这篇文章的方法不是很好理解, 代码也刚开源, 做一下笔记备忘.
0. Abstract
传统的光流或者粒子视频跟踪方法都是用有限的时间窗口去解决的, 所以他们并不能很好的应对长时遮挡, 也不能保持估计的轨迹的全局连续性. 为此, 我们提出了一个完整的, 全局的连续性的运动表示方法, 叫做OmniMotion. 具体地, OmniMotion将一个视频序列表示成一个准-3D的规范量(quasi-3D canonical volume), 然后通过定义一个双射(也就是从平面空间到所谓的canonical的空间), 这样我们通过一个准3D空间, 就可以描述一个完整的运动(因为补偿了2D缺失的信息).
1. Method
由于对相关领域知识的匮乏, 先略过Introduction和Related Work部分, 先来看方法.
从整体流程上, OmniMotion将一整个视频序列作为输入, 同时还输入不太准确的带噪的运动估计(例如光流估计), 然后解出一个完整的, 全局的运动轨迹.
那么如何解决遮挡问题呢? 遮挡, 只是在2D的图像平面下遮挡了, 但是在3D信息中是可以恢复出来的. 为此, 我们将场景给投影到某个3D空间, 这个空间可以尽可能描述像素完整的运动. 比如说, 第 t 1 t_1 t1帧的某个像素 x 1 x_1 x1, 给投影到这个3D空间变为 x ′ x' x′, 然后在第 t 2 t_2 t2帧我们再将这个 x ′ x' x′投射到2D平面, 就得到了对应的点 x 2 x_2 x2. 由于这个3D不需要真正的进行3D重建(因为真正的3D重建是需要知道相机的内参和外参, 内参包括图像中心的坐标, 相机的焦距等, 外参需要知道相机的朝向等, 是比较复杂的), 因此我们将该空间成为quasi-3D.
所以具体是如何做的呢?
1.1 规范3D量的组成
我们将前述的规范3D量记为 G G G. 和神经辐射场(NeRF)一样, 我们在 G G G上定义了一个基于坐标的网络 F θ F_{\theta} Fθ, 该网络将 G G G中的3D坐标 u u u映射到密度 σ \sigma σ和颜色 c c c. 其中密度可以告诉我们表面(surface)在这个3D空间中的位置, 颜色是可以在训练过程中计算光度损失(photometric loss).
1.2 3D双射
如前所述, 我们需要定义一个从本地坐标(也就是视频或图像坐标)到quasi-3D空间的一个映射, 以及逆映射, 这样我们可以再映射回别的时间索引的帧找到对应点. 然而, 实际上该工作是将本地的2D坐标给提升到3D的(后面会讲如何做的), 然后从提升后的本地3D坐标投影到quasi-3D空间. 整个映射和逆映射的过程如下:
x j = T j − 1 ∘ T i ( x i ) x_j = \mathcal{T}_j^{-1}\circ \mathcal{T}_i(x_i) xj=Tj−1∘Ti(xi)
其中 i , j i,j i,j是frame index, 因此, 我们定义的映射是和时间有关的. 然而, 中间产物 u = T i ( x i ) u= \mathcal{T}_i(x_i) u=Ti(xi)应该是与时间无关的.
在实现上, 映射是用可逆神经网络(INN)做的.
1.3 计算运动
流程上, 我们在2D图像上的一个像素 p i p_i pi, 我们首先将其提升到3D, 变成 p i ′ p_i' pi′. 方法是在一个射线上进行采样. 然后用上一节定义的3D双射投影到第 j j j帧对应的3D点, 最后再降维回2D就可以了.
具体地, 由于我们已经将相机的运动包含在映射 T \mathcal{T} T内了 , 因此我们直接将相机建模成固定的正交相机. 固定正交相机的含义是, 物体不再具有近大远小的特征. 这样一来, 我们就可以很容易的将2D坐标拓展到3D坐标. 也就是说, 既然物体的大小不再随着深度的变化而变化, 那么2D像素点 ( x i , y i ) (x_i, y_i) (xi,yi)不论深度如何, 它的值(RGB)一直是一样的, 因此前述的射线可以这样定义:
r i ( z ) = o i + z d , o i = [ p i , 0 ] ∈ R 3 , d = [ 0 , 0 , 1 ] r_i(z)=o_i+zd, \\ o_i = [p_i, 0] \in \mathbb{R}^3, d = [0, 0, 1] ri(z)=oi+zd,oi=[pi,0]∈R3,d=[0,0,1]
因此我们在这个射线上采集 K K K个样本, 就相当于在这个固定正交相机拍摄的3D场景中进行深度采样.
然后, 这么一堆样本, 我们用映射 T i \mathcal{T}_i Ti投影到quasi-3D空间, 然后再用之前说的映射 F θ F_{\theta} Fθ转换成密度和颜色的量 ( σ , c ) (\sigma, c) (σ,c), 即, 对于第 k k k个样本:
( σ k , c k ) = F θ ( T i ( x i k ) ) x j k = T j − 1 ( ( σ k , c k ) ) (\sigma_k, c_k) = F_\theta(\mathcal{T}_i(x_i^k)) \\ x_j^k = \mathcal{T}_j^{-1}((\sigma_k, c_k)) (σk,ck)=Fθ(Ti(xik))xjk=Tj−1((σk,ck))
随后, 我们根据第 j j j帧的这 K K K个对应样本, 得到第 j j j帧的估计:
x ^ j = ∑ k = 1 K T k α k x j k , where T k = Π l = 1 k − 1 ( 1 − α l ) , α k = 1 − exp { − σ k } \hat{x}_j = \sum_{k=1}^KT_k\alpha_kx_j^k, \\ \text{where} ~~T_k=\Pi_{l=1}^{k-1}(1-\alpha_l), \\ \alpha_k = 1-\exp\{-\sigma_k\} x^j=k=1∑KTkαkxjk,where Tk=Πl=1k−1(1−αl),αk=1−exp{−σk}
以上的过程叫做alpha compositing, 是NeRF中一个常用的技巧. 意义是, 密度实际上表达了3D空间中存在物体的可能性, 1 − exp { − σ k } 1-\exp\{-\sigma_k\} 1−exp{−σk}就是一种对概率的衡量. 对于是否采纳第 k k k个样本, 重要性为 T k α k T_k\alpha_k Tkαk, α k \alpha_k αk已经解释. T k T_k Tk的含义是在这之前的样本的联合可信程度, 也就是说, 之前有一个样本已经比较可信了, 那么这个样本就可以更少的采纳.
以上是个人理解
因此, 上面的过程总结为下图:
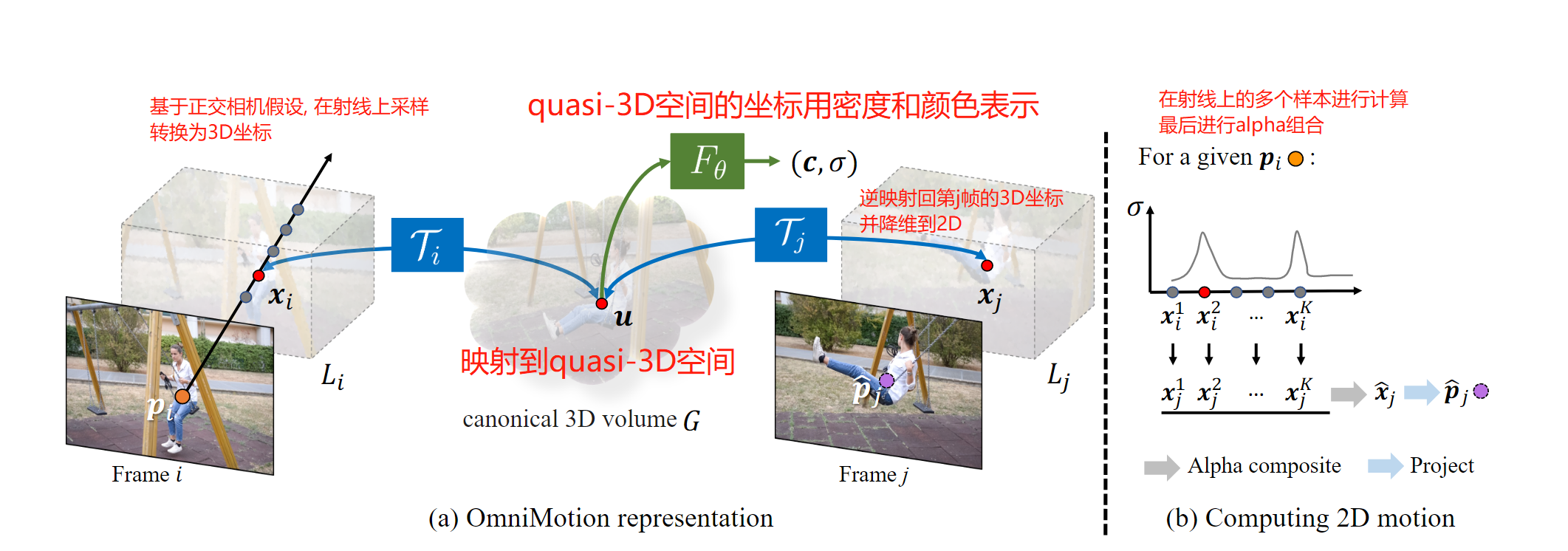
2. Training
这个工作是用已有的光流方法生成标签, 指导训练的. 这部分重点先记一下损失函数.
损失函数由三部分构成, 一个是位置误差, 也就是坐标误差. 一个是颜色误差, 这就是前面 c c c的作用, 还有一个是因为要保证平稳性而加入的罚项. 其中1, 3项采用1范数, 第二项采用2范数.
Flow loss:
L f l o = ∑ f i → j ∣ ∣ f ^ i → j − f i → j ∣ ∣ 1 , f ^ i → j = p ^ j − p i \mathcal{L}_{flo} = \sum_{f_{i \to j}}|| \hat{f}_{i \to j} - f_{i \to j}||_1, \\ \hat{f}_{i \to j} = \hat{p}_j - p_i Lflo=fi→j∑∣∣f^i→j−fi→j∣∣1,f^i→j=p^j−pi
photometric loss:
L p h o = ∑ i , p ∣ ∣ C ^ i ( p ) − C i ( p ) ∣ ∣ 2 2 \mathcal{L}_{pho} = \sum_{i, p}|| \hat{C}_{i}(p) - C_i(p)||_2^2 Lpho=i,p∑∣∣C^i(p)−Ci(p)∣∣22
smooth loss:
L r e g = ∑ i , x ∣ ∣ x i + 1 − x i + x i − 1 − x i ∣ ∣ 1 \mathcal{L}_{reg} = \sum_{i, x}|| x_{i + 1} - x_i + x_{i - 1} - x_i||_1 Lreg=i,x∑∣∣xi+1−xi+xi−1−xi∣∣1
意义是保证前一帧和后一帧的差距尽量小.
最终的loss是这三项的线性组合.