一、快速排序的介绍
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中 的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右 子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。(其时间复杂度最优为N*logN,空间复杂度最优为lonN,这里就不予证明了!过程相当复杂!)
用一种通俗的话来讲快速排序其实就时设定一个界定值,然后分别开始遍历需要排序的元素,将小于该界定值和大于该界定值的放在其两侧,每次结束都能将该界定值放到其最终正确的位置!
二、快速排序的思想
快速排序其思想也是采用了分治的思想,将一个大问题转化为若干个小问题,然后逐个解决每个小问题,最终达到解决问题的目的!
三、快速排序的实现
由上面内容可以知道,若想实现快速排序,则可以先执行单个元素的排序,然后再进行递归处理解决整组数据的排序!因为快速排序是一种二叉树结构的交换排序,所以可以采用递归的方法将其解决!

下面来看一下如何实现单趟排序,让数据中一个元素位于其最终应处于的位置!
单趟排序的实现
注:本篇文章例子是以默认排升序,若要实现降序仅需要将循环条件改变一下即可!
法一:(霍尔思想)
其单趟排序的思想就是假定一个界定值,然后左右两边开始遍历,若要排升序,则左边找到的比界定值大的值就停下,右边找到比界定值小的就停下,然后交换两者的值,当左右两边相遇时,就结束循环,最后将相遇的位置的值与界定值交换位置即可完成本次界定值的最终位置的实现!
//注意:因为这是单趟排序,保证了界定值处于该数据最终所在的位置,所以该函数应返回本次界定值的位置,方便下次调用这个函数实现递归调用解决其另外界定值最终的位置!
画个图来形象的描述一下该过程是如何实现的吧!

代码如下:
int Hoare(int* a, int left,int right)
{
int vali = left;
while (left < right)
{
//若没有left<right这个限制条件,那么当从左边开始走的时候其对应的值一直小于a[vali]时,则会导致越界问题!
//注意若选取vali在左边,那么从右边先走,因为从右边先走才能保证最后相遇的位置一定是小于vali的值,因为从右边找
//的话是找比val小于或等于的值停下来!
while (left < right && a[right] >= a[vali])
{
right--;
}
while (left < right && a[left] <= a[vali])
{
left++;
}
swap(&a[left], &a[right]);
}
//因为最后left和right相遇,所以只需将a[vali]与二者任意一个交换位置即可!
swap(&a[left], &a[vali]);
return left;
}注意:(1)该函数的实现需要注意的是,必须保证里面的循环条件是left<right,因为假设当从左边开始时,其后面的值一直小于等于val时,则会导致left越界,进而导致程序错误!
(2)还需要注意一点的是,当选的界定值在左边时,那么必须从右边开始遍历,因为从右边先走可以保证最终左边相遇右边时,其遇到的右边一定是小于val的值,因为当最后左边和右边相遇时,还需要交换左边或右边的值与val的值,若交换的值大于val时,交换之后则没有排序成功,反之,若选的界定值在右边时,那么必须从左边开始遍历,原理同上!
法二(挖坑大法!)
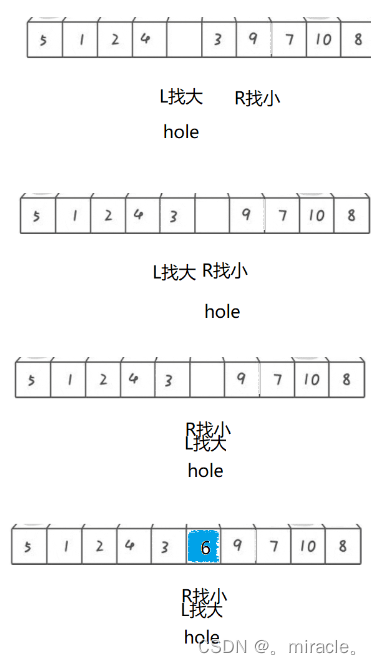
原理如下:挖坑大法的原理就是选定一个界定值,将其保存起来,然后将其位置假设为一个坑,然后左右两边分别开始遍历,当左边找到比界定值大的值时,则将其数据填入坑中,坑的位置更新为新填入数据原来的位置,当右边位置找到比界定值小的值时,也将其数据填入坑中,坑的位置更新为新填入数据原来的位置!最后当左右相遇时,它们相遇一定是在坑中相遇,将原来界定值存放到坑中,此时界定值与其左右两边数据保持相对有序!图像如下:
注:这里假定坑位为左边第一个数据!那么就必须从右边开始先遍历,原因与法一相同!

代码如下:
int hole (int* a, int left, int right)
{
int hole = left;
int val = a[left];
while (left < right)
{
//先从右边开始找比val小的值,找到后把坑填了,然后其位置就成为新的坑位!
while (left < right && a[right] >= val)
{
right--;
}
a[hole ] = a[right];
hole = right;
while (left < right && a[left] <= val)
{
left++;
}
a[hole ] = a[left];
hole = left;
}
a[hole ] = val;
return left;
}法三:双指针
原理:定义两个快慢指针,当快指针指向的值小于界定值时,让慢指针向后走一步,然后交换快慢指针对应的值,不管如何快指针是都要向后走的,只有当快指针的值小于val时,慢指针才会向后走一步,然后与其值交换!最后当快指针走完整个数据循环结束!从其思想上面可以看出,当快慢指针之间的值都是比界定值大的数据,因为只有当指针指向的值小于界定值时,慢指针才会向后走,并与当前快指针指向的小于界定值的数据与前面的慢指针的值进行交换!
图像如下:

从图中可以看出,fast和slow之间的值都是大于界定值的!所以当fast找到比界定值小的数值后,进行slow++操作,然后交换二者位置,仍然可以保证 fast和slow之间的值还都是大于界定值!
代码如下:
int Dpointer(int* a, int left, int right)
{
int slow = left;
int fast = left + 1;
int vali = left;
while (fast<=right)
{
if (fast!=++slow && a[fast] < a[vali])//当slow++的位置和fast位置相同时就没必要进行交换了!
{
slow++;
swap(&a[fast], &a[slow]);
}
fast++;
}
//注意一定要交换slow当前的值与原vali的值,然后将vali的位置重新赋值为slow的位置!
swap(&a[slow], &a[vali]);
vali = slow;
return vali;
}以上三种方法都是单趟的排序,因为快排是一种二叉树结构的交换排序方法,所以要想将所有元素进行排序,就可以采用递归的方法进行操作,从而完成整组数据的排序!
整组数据的排序实现!
代码如下:
void Qsort(int* a, int left, int right)
{
//控制当区间不存在时,则跳出递归!
if (left >= right)
{
return;
}
/*int vali = Hoare(a, left,right);*/
//int vali = hig(a, left,right);
int vali = Dpointer(a, left, right);
Qsort(a, left, vali - 1);
Qsort(a, vali+1, right);
}当第一个排过序后,其第一个界定值就处于其最终存在的位置,所以可将界定值左边的元素再次进行一次排序,从而找到下一个界定值最终处于的位置,直至最后所要排序的区间不存在,排序即完成!
今日的快排分享到此为止,如有小伙伴还有不懂的地方欢迎在评论区留言提问哦!