常见的非线性灰度变换为对数变换和幂次变换。

对数变换

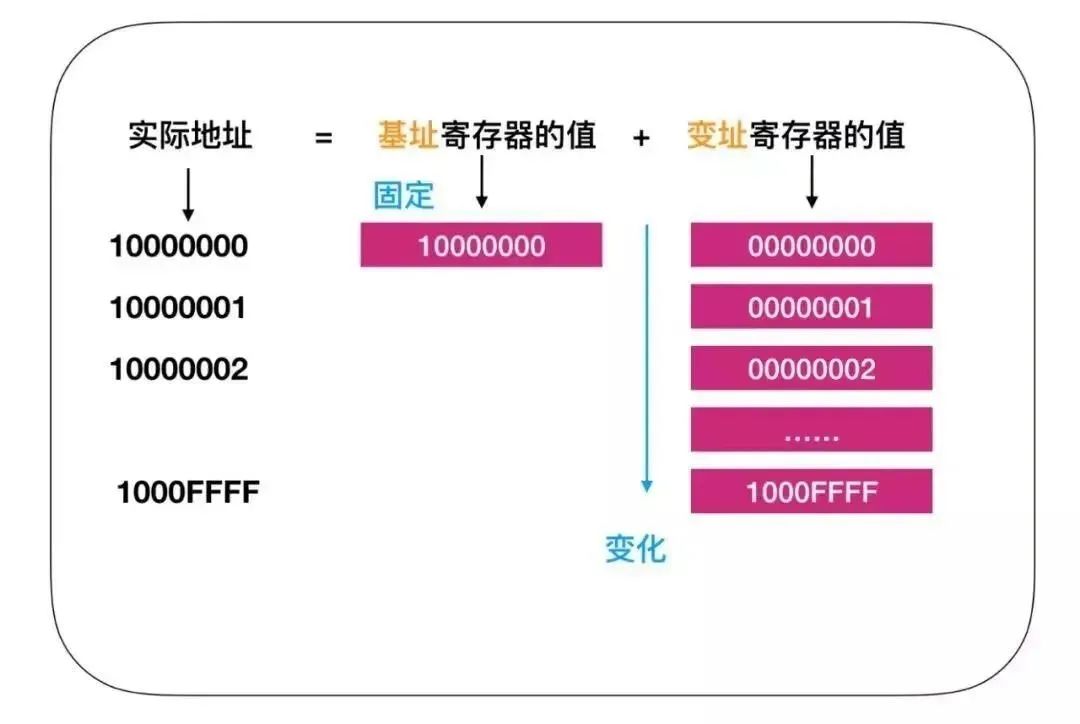
对数变换的一般表达式为：

t=clog(1+s)                             

其中c为尺度比例常数，s为输入图像灰度值，t为变换后的输出图像灰度值。在如下图所示的对数曲线上，函数自变量低值时，曲线的斜率很高;自变量高值时，曲线斜率变小。

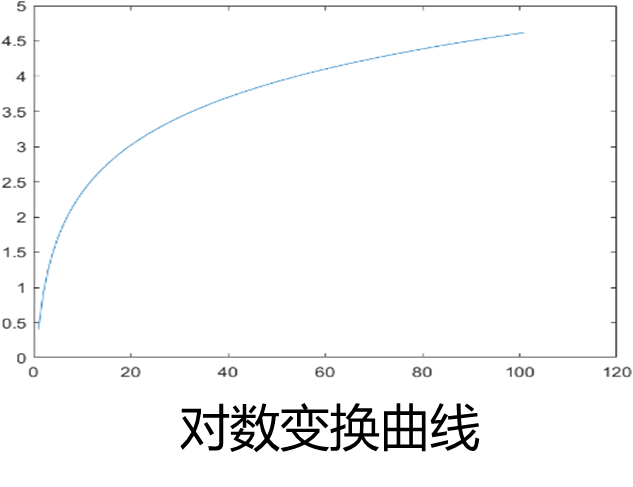
对数变换的作用

1.对数变换可以增强一幅图像中较暗部分的细节，从而可用来扩展被压缩的高值图像中的较暗像素，因此对数变换被广泛地应用于频谱图像的显示中。一个典型的应用是傅立叶频谱（参见第5章)，其动态范围可能宽达0~10610^6。

2.使用对数变换，图像的动态范围被合理地非线性压缩，从而可以清晰地显示。

指数变换

指数变换又名幂次变换或伽马变换，其表达式的一般形式为：

                              

其中，c和γ为正常数。

指数变化的作用

与对数变换不同，指数变换可以根据γ的不同取值选择性地增强低灰度区域的对比度或是高灰度区域的对比度。

（1）当γ <1时，效果和对数变换相似，放大暗处细节，压缩亮处细节，随着数值减少，效果越强。

（2）当γ >1时，放大亮处细节，压缩暗处细节，随着数值增大，效果越强。

（3）当γ =1时，t=cs，这操作的得到的输出图像是线性的。

作为r的函数，s对于γ的各种值绘制的曲线如图所示，从上到下γ分别为0.04、0.1、0.2、0.4、0.67、1、1.5、2.5、5、10、25。像对数变换的情况一样，幂次曲线中γ的部分值把输入窄带暗值映射到宽带输出值。相反，输入高值也成立。当 c=γ=1时，将简化为线性变换。如下图所示：

示例程序

%c=1，γ分别为0.5、2和5时对图像进行变换的程序
I = imread('printedtext.png');
J = imadjust(I,[],[],0.5);  %放大暗处细节，压缩亮处细节。
K = imadjust(I,[],[],2);  %放大亮处细节，压缩暗处细节。
L = imadjust(I,[],[],5);  %放大亮处细节，压缩暗处细节。
subplot(2,2,1),imshow(I);title('原图像');
subplot(2,2,2),imshow(J);title('γ=0.5');
subplot(2,2,3),imshow(K);title('γ=2');
subplot(2,2,4),imshow(L);title('γ=5’);

 结果图片