题目

题解一:暴力双指针—超时了
双指针暴力查找(需考虑begin == end 和begin == end ==i) 的情况 ----- 力扣示例超出时间限制
public int[] productExceptSelf(int[] nums) {
int length = nums.length;
int begin = 0;
int end = length -1;
int i = 0;
int[] number = new int[length];
int sum = 1;
while(i<length){
if (begin == i) {
begin++;
continue;
}
if (end == i) {
end--;
continue;
}
if (begin < end) {
sum *= nums[begin]*nums[end];
begin ++ ;
end -- ;
}else if(begin == end){
number[i] =sum * nums[begin] ;
begin =0;
end = length -1;
i++;
sum =1;
continue;
}else if(begin > end ){
number[i] =sum;
begin =0;
end = length -1;
i++;
sum =1;
continue;
}
}
return number;
}
题解二:左右乘积之积
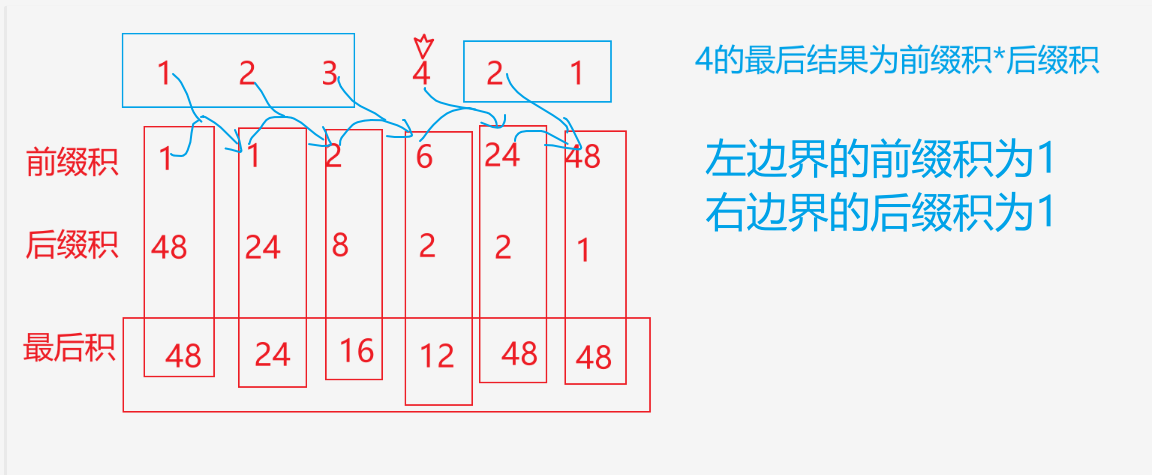
方法二: 左右乘积之积 = 除自身以外数组的乘积 分别计算左右乘积再最后相乘
public int[] productExceptSelf(int[] nums) {
// 1 2 3 4
// (1*2)3 4 3------> 前缀积(1*2) * 4后缀积
int length = nums.length;
// L 和 R 分别表示左右两侧的乘积列表
int[] left = new int[length];
int[] right = new int[length];
//计算左前缀乘积
// L[i] 为索引 i 左侧所有元素的乘积
// 对于索引为 '0' 的元素,因为左侧没有元素,所以 L[0] = 1
left[0] = 1;
for(int i=1 ;i< length ;i++){
left[i] = nums[i-1] * left[i-1];
}
// R[i] 为索引 i 右侧所有元素的乘积
// 对于索引为 'length-1' 的元素,因为右侧没有元素,所以 R[length-1] = 1
right[length -1] = 1;
for(int i=length-2 ;i>= 0 ;i--){
right[i] = nums[i + 1] * right[i +1];
}
// 对于索引 i,除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
int[] answaer = new int[length];
for(int i =0;i<length;i++){
answaer[i] = right[i] * left[i];
}
return answaer;
}
题解三:左右乘积之积 —优化空间复杂度(O(1))
相比较上面的做法,使用最终答案数组代替其中一个缀积,然后再计算缀积相乘的时候,使用一个累乘变量来记录某一个前缀和,最后只开辟了一个数组来存最终答案,复杂度为O(1)
// 方法三: 优化左右乘积之积 使得最后答案数组提前存储 前缀或后缀之积,这样就可以减少开辟一个数组 降低空间复杂度
public int[] productExceptSelf(int[] nums) {
int length = nums.length;
int[] answer = new int[length];
// answer[i] 表示索引 i 左侧所有元素的乘积
// 因为索引为 '0' 的元素左侧没有元素, 所以 answer[0] = 1
answer[0] = 1;
for (int i = 1; i < length; i++) {
answer[i] = nums[i - 1] * answer[i - 1];
}
// R 为右侧所有元素的乘积
// 刚开始右边没有元素,所以 R = 1
int R = 1;
for (int i = length - 1; i >= 0; i--) {
// 对于索引 i,左边的乘积为 answer[i],右边的乘积为 R
answer[i] = answer[i] * R ;
// R 需要包含右边所有的乘积,所以计算下一个结果时需要将当前值乘到 R 上
R = R *nums[i]; //同步记录下一个元素的前缀和
}
return answer;
}
}