目录

深度学习优化入门：Momentum、RMSProp 和 Adam

病态曲率

1牛顿法

2 Momentum:动量

3Adam

---

深度学习优化入门：Momentum、RMSProp 和 Adam

 

本文，我们讨论一个困扰神经网络训练的问题，病态曲率。

虽然局部极小值和鞍点会阻碍我们的训练，但病态曲率会减慢训练的速度，以至于从事机器学习的人可能会认为搜索已经收敛到一个次优的极小值。让我们深入了解什么是病态曲率。

「病态曲率」

考虑以下损失曲线图。

 

病态曲率

如你所知，我们在进入一个以蓝色为标志的像沟一样的区域之前是随机的。这些颜色实际上代表了在特定点上的损失函数的值，红色代表最高的值，蓝色代表最低的值。

我们想要下降到最低点，因此，需要穿过峡谷。这个区域就是所谓的病态曲率。为了了解为何将其称为病态曲率，让我们再深入研究。放大了看，病态曲率就像这样...

要知道这里发生的事情并不难。梯度下降沿着峡谷的山脊反弹，向最小的方向移动的速度非常慢。这是因为山脊的曲线在 W1 方向上弯曲的更陡。

考虑山脊表面的 A 点。我们看到，梯度在这点可以分解为两个分量，一个沿着 W1 方向，另外一个沿着 W2 方向。如果 f 显著下降的唯一方向是低曲率的，那么优化可能会变得太慢而不切实际，甚至看起来完全停止，造成局部最小值的假象。

 

正常情况下，我们使用一个较慢的学习率来解决这种山脊间反弹的问题，正如上一篇关于梯度下降的文章所述。然而，这却产生了麻烦。

当我们接近最小值时，慢下来是有意义的，我们想要收敛于它。但是考虑一下梯度下降进入病态曲率的区域，以及到最小值的绝对距离。如果我们使用较慢的学习率，可能需要花费更多的时间才能到达极小值点。事实上，有研究论文报道过使用足够小的学习率来阻值山脊间的反弹可能导致参与者以为损失根本没有改善，从而放弃训练。

如果 f 显著下降的唯一方向是低曲率的，那么优化可能会变得太慢而不切实际，甚至看起来完全停止，造成局部最小值的假象。

也许我们想要的是能让我们慢慢进入病态曲率底部的平坦区域，然后在最小值的方向上加速。二阶导数可以帮助我们做到这一点。

1牛顿法

梯度下降是一阶优化方法。它只考虑损失函数的一阶导数，而不考虑更高阶的导数。这基本上意味着它不知道损失函数的曲率。它只能说明损失是否下降以及下降的速度，而不能区分曲线是平坦的，向上的，还是向下的。

 

之所以会发生这种现象，是因为梯度下降只关心梯度，就好像上图中红色的点，三个曲线在这一点上的梯度是相同的。如何解决？使用二阶导数，或者考虑梯度变化的速率。

一个非常流行的可以使用二阶导数的技术，可以解决我们的问题，这个方法称为牛顿法。 如果表面变得不那么陡峭，那么学习步骤就会减少。

牛顿法可以提供一个理想的步长，在梯度方向上移动。由于我们现在有了关于损失表面曲率的信息，所以可以选择步长，而不是用病态曲率来超过该区域的极限。

牛顿法通过计算 Hessian 矩阵来实现，Hessian 矩阵是损失函数的二阶导数组成的权值组合。我所说的权值组合，如下所示。

 

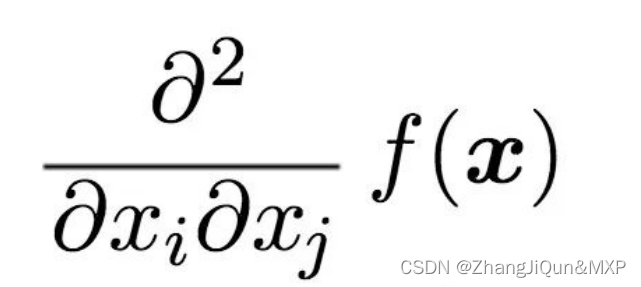
Hessian 矩阵在一个大矩阵中计算所有这些梯度。

 

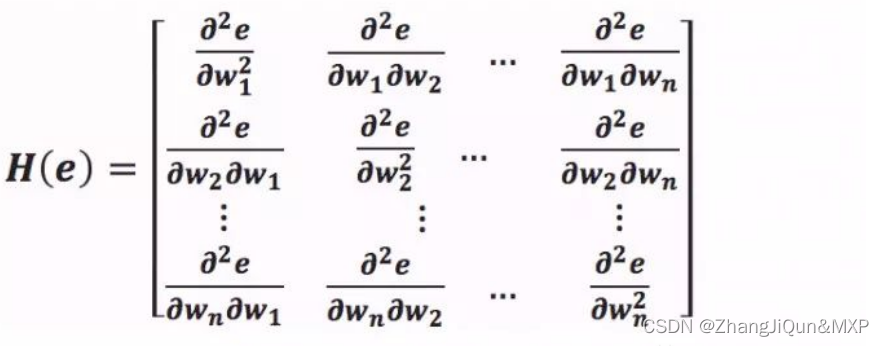
Hessian 矩阵给出了一个点的损失曲面曲率的估计。一个损失的表面可以有一个正曲率，这意味着当我们移动时，表面会迅速变得不那么陡峭。如果我们有一个负曲率，这意味着当我们移动时，曲面变得越来越陡。

 

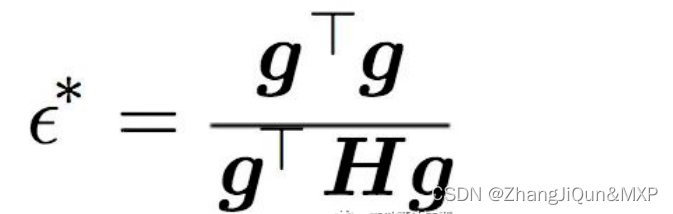
注意，如果这一步是负的，那就意味着我们可以使用任意的步骤。换句话说，我们可以切换回原来的算法。这对应于下面的情况，梯度变得越来越陡。

然而，如果梯度变得不那么陡峭，我们可能会走向一个处于病态曲率底部的区域。在这里，牛顿法给了我们一个修正的学习步骤，正如你所看到的，它与曲率成反比，或者曲面变得越来越小。

如果表面变得不那么陡峭，那么学习步骤就会减少。

2 Momentum:动量

与 SDG 结合使用的一种常用方法叫做 Momentum。Momentum 不仅会使用当前梯度，还会积累之前的梯度以确定走向。梯度下降方程修改如下。

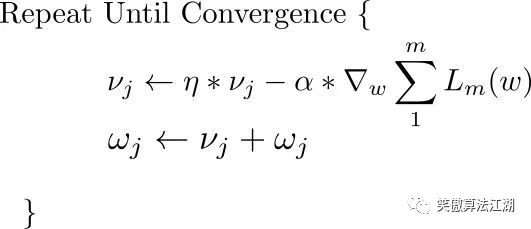
第一个式子有两项。第一项是上一次迭代的梯度，乘上一个被称为「Momentum 系数」的值，可以理解为取上次梯度的比例。

我们设 v 的初始为 0，动量系数为 0.9，那么迭代过程如下：

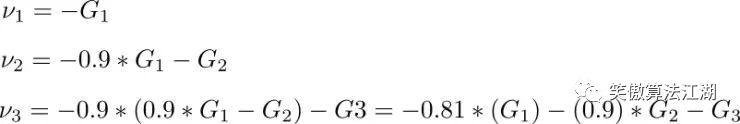
我们可以看到之前的梯度会一直存在后面的迭代过程中，只是越靠前的梯度其权重越小。（说的数学一点，我们取的是这些梯度步长的指数平均）。

这对我们的例子有什么帮助呢？观察下图，注意到大部分的梯度更新呈锯齿状。我们也注意到，每一步的梯度更新方向可以被进一步分解为 w1 和 w2 分量。如果我们单独的将这些向量求和，沿 w1 方向的的分量将抵消，沿 w2 方向的分量将得到加强。

3Adam

到目前为止，我们已经对比了 RMSProp 和 Momentum 两种方法。尽管 Momentum 加速了我们对极小值方向的搜索，但 RMSProp 阻碍了我们在振荡方向上的搜索。

Adam 或 Adaptive Moment Optimization:自适应力矩优化. 算法将 Momentum 和 RMSProp 两种算法结合了起来。这里是迭代方程。

我们计算了每个梯度分量的指数平均和梯度平方指数平均（方程 1、方程 2）。为了确定迭代步长我们在方程 3 中用梯度的指数平均乘学习率（如 Momentum 的情况）并除以根号下的平方指数平均（如 Momentum 的情况），然后方程 4 执行更新步骤。

超参数 beta1 一般取 0.9 左右，beta_2 取 0.99。Epsilon 一般取1e-10。

「结论」

在这篇文章中，我们介绍了 3 种基于梯度下降法来解决病态曲率同时加快搜索速度的方法。这些方法通常称为「自适应方法」，因为学习步骤会根据等高线拓扑进行调整。

在上面的三种方法中，尽管 Adam 算法在论文中被认为是最有前景的算法，但是 Momentum 方法貌似更主流一些。实践结果表明，在给定损失函数的情况下，三种算法都能收敛到不同的局部最优极小值。但是用带 Momentum 的 SGD 算法比 Adam 算法找到的极小值更加平坦，而自适应方法往往会收敛到更加尖锐的极小值点。平坦的极小值通常好于尖锐的极小值。

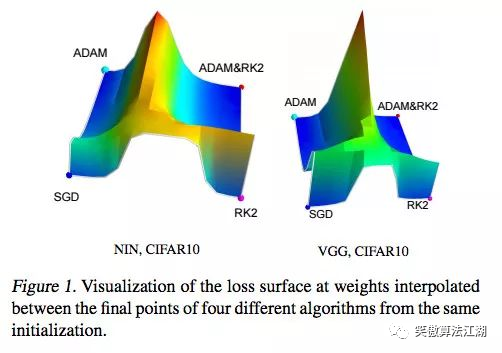
尽管自适应算法有助于我们在复杂的损失函数上找到极小值点，但这还不够，特别是在当前网络越来越来越深的背景下。除了研究更好的优化方法之外，还有一些研究致力于构建产生更平滑损失函数的网络架构。Batch-Normalization 和残差连接是其中的解决方法，我们也会尽快在博客上发布有关的详细介绍。欢迎随时在评论中提问。