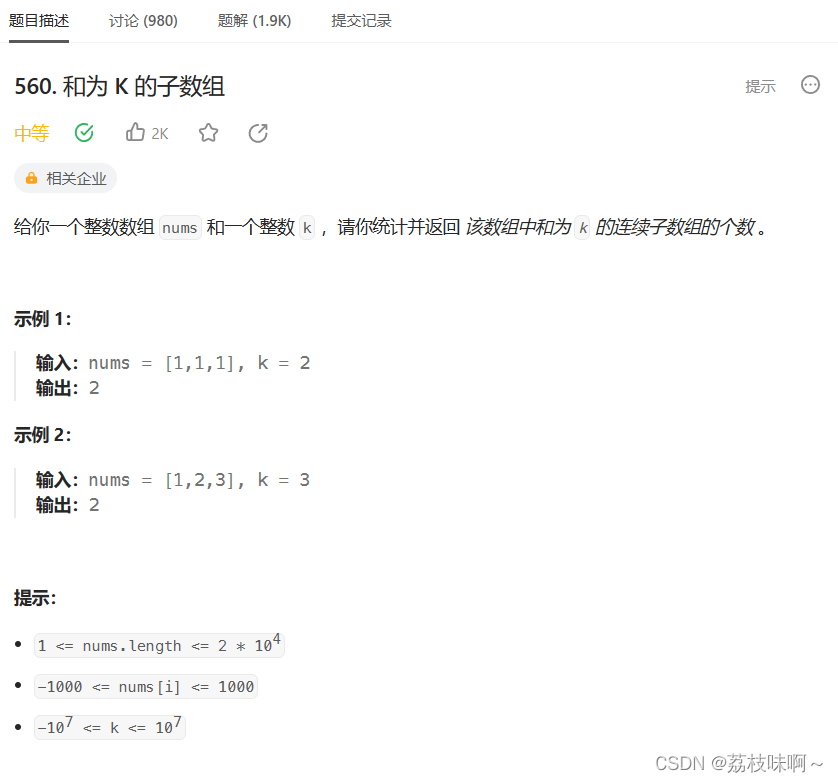
这道题我用的是暴力法，当然也是不断的提交不断发现问题改出来的，比如我之前是算到和大于目标值就break，其实不行因为后面还可以有负数，我把break删了。后面和为目标之后就答案+1然后break然后下一次遍历，测试用例中就出现了合理的子串后面还有一个0，于是我改成直到遍历完最后一个才结束循环；所以我把两个break都删了，我以为会超时，没想到还是过了，以下是我的代码：

class Solution {
    public int subarraySum(int[] nums, int k) {
       int ans =0;
       int n = nums.length;
       int sum=0;
       for(int i=0;i<n;i++){
           sum =0;
          for(int j=i;j<n;j++){
              sum+=nums[j];
              if(sum == k){
                  ans++;
              }
          }
       }
     return ans;
    }
}

就是最简单的暴力法，用i，j两个指针作为子串的起点和终点，然后把子串的所有数的和加起来，如何等于k，ans++。这里就需要注意我前面提到的无论sum=k还是sum>k都不能break，要遍历到最后一个数自动结束，外层循环每次sum归0。

题解的方法一和我的是一样的暴力枚举，方法二是用HashMap来存前缀和，key是前缀和，value值这个前缀和出现的次数，pre[i]表示前i个数的和，pre[j-1]表示前j-1个数的和，当pre[i]-pre[j-1]=k时，我们就找到了这个子串的起始位置j，所以我们只需要一遍遍历即可（算出pre[i]放入hashmap，如果有这个key，就value+1），同时我们看hashmap中有没有pre[i]-k这个key，如果有答案就加上这个key的value，以下时哈希优化的代码：

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0, pre = 0;
        HashMap < Integer, Integer > mp = new HashMap < > ();
        mp.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            pre += nums[i];
            if (mp.containsKey(pre - k)) {
                count += mp.get(pre - k);
            }
            mp.put(pre, mp.getOrDefault(pre, 0) + 1);
        }
        return count;
    }
}