文章目录
- 不重复数组找最小值,返回下标
- 重复数组找最小值,返回下标
- 不重复数组找target,返回下标
- 重复数组找target,返回bool
- 重复数组找target,返回下标
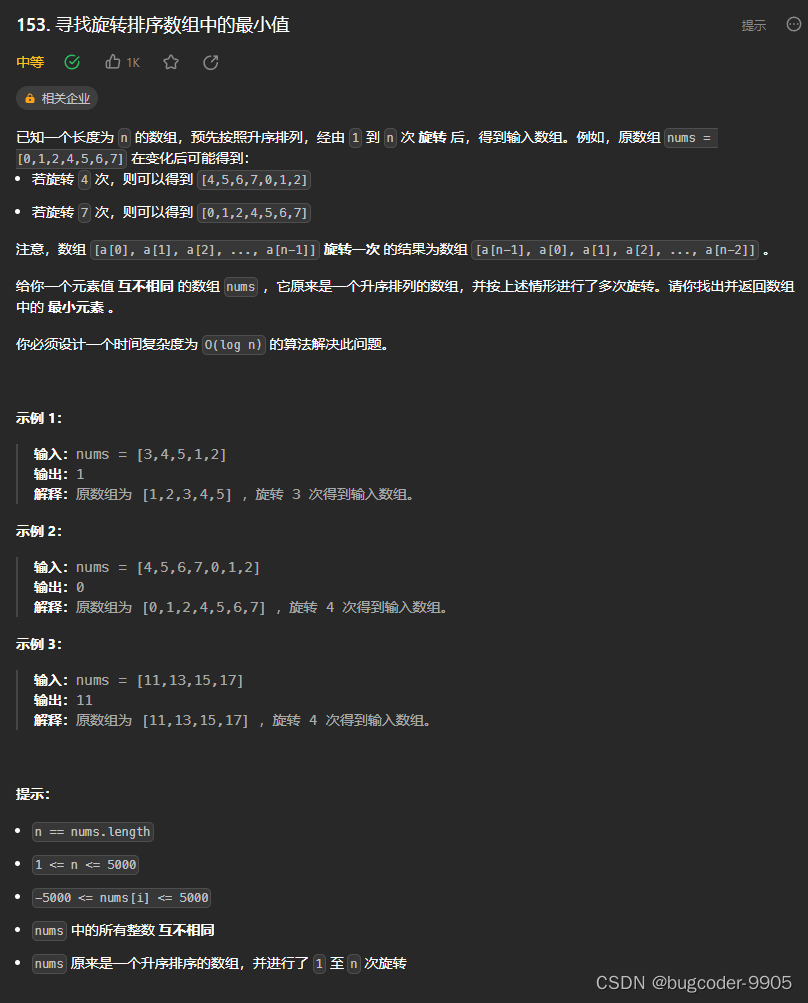
不重复数组找最小值,返回下标
class Solution {
public int findMin(int[] nums) {
int n = nums.length;
int l = 0;
int r = n - 1;
while(l <= r){
if(l == r || nums[l] < nums[r]){
break;
}
int mid = l + (r - l) / 2;
if(nums[mid] >= nums[l]){
// [l, mid]有序
l = mid + 1;
}else{
// [mid, r]有序
r = mid;
}
}
return nums[l];
}
}
class Solution {
public int findMin(int[] nums) {
int n = nums.length;
int l = 0;
int r = n - 1;
while(l <= r){
if(l == r || nums[l] <= nums[r]){
// [l,r]已经有序
break;
}
int mid = l + (r - l) / 2;
if(nums[mid] > nums[l]){
l = mid + 1;
}else if(nums[mid] < nums[l]){
r = mid;
}else{
l++;
}
}
return nums[l];
}
}
重复数组找最小值,返回下标
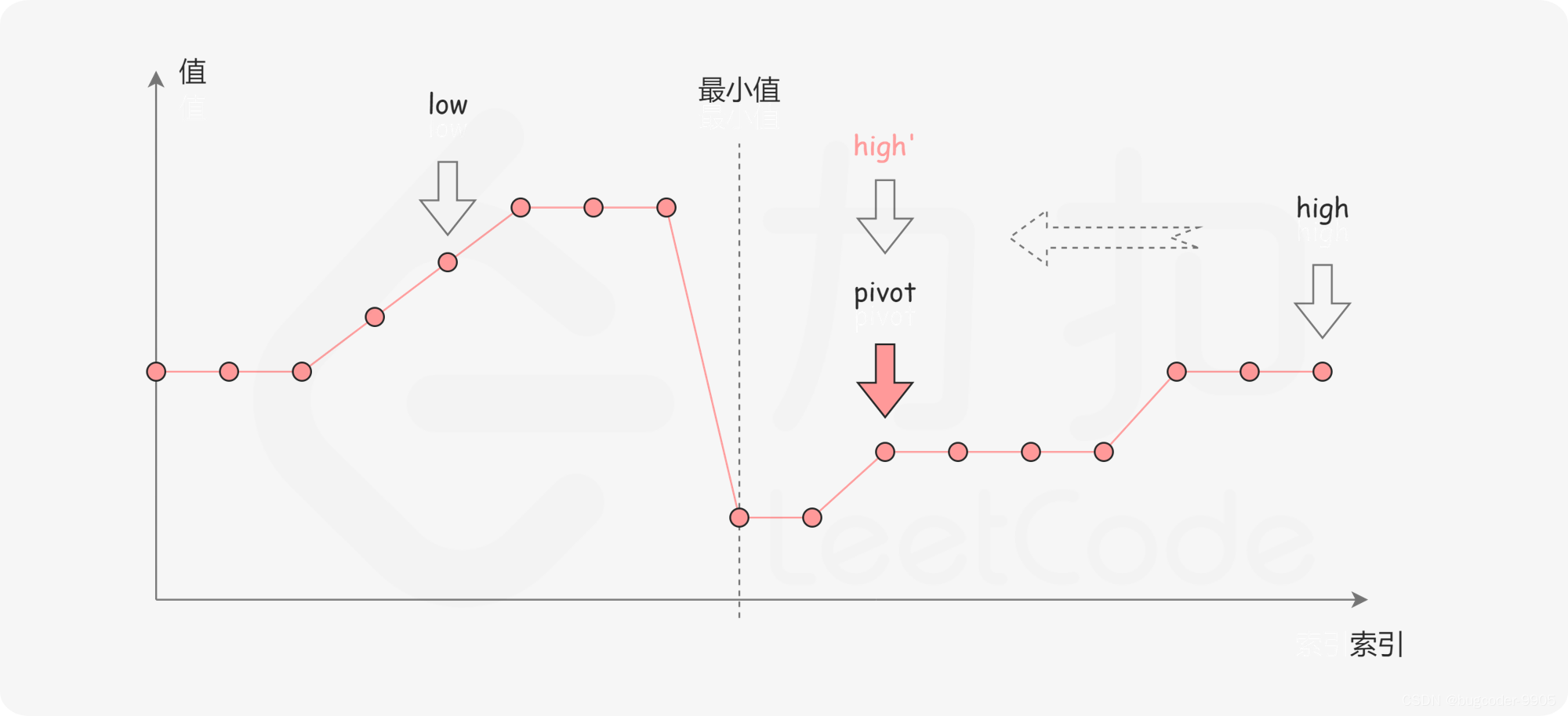
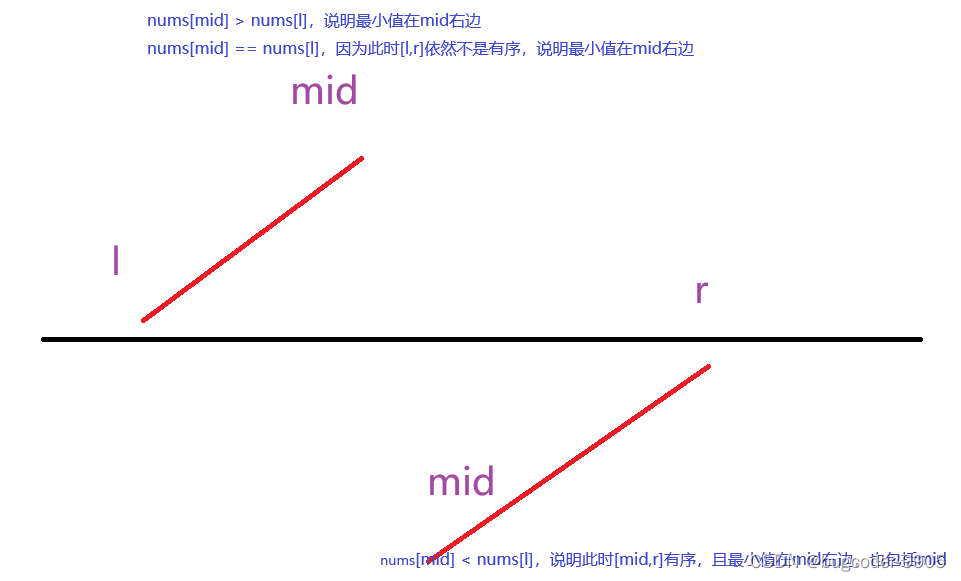
nums[mid] < nums[l],说明最小值肯定在(low, mid]区间内,则r = mid
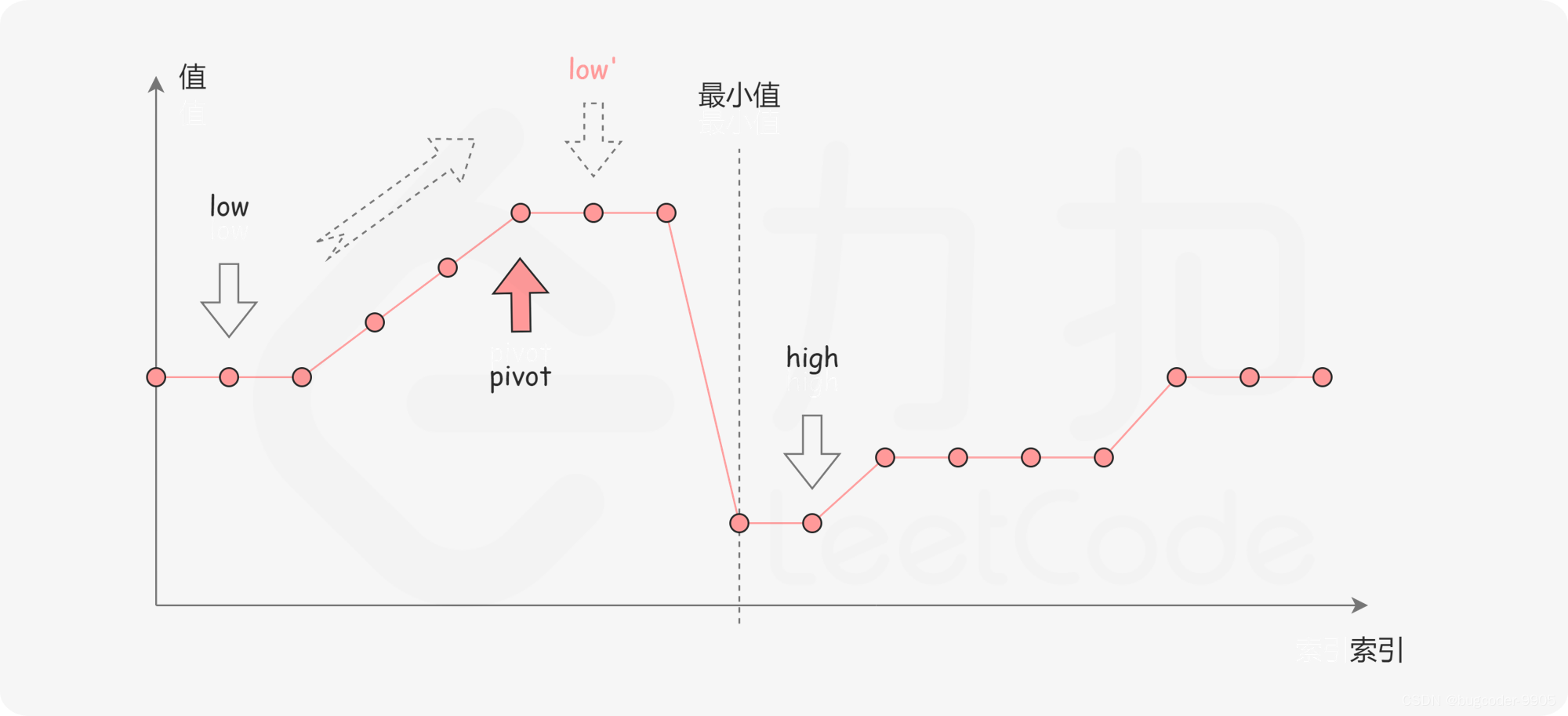
nums[mid] > nums[l],说明最小值肯定在mid右侧,(mid,r]区间内,则l = mid + 1
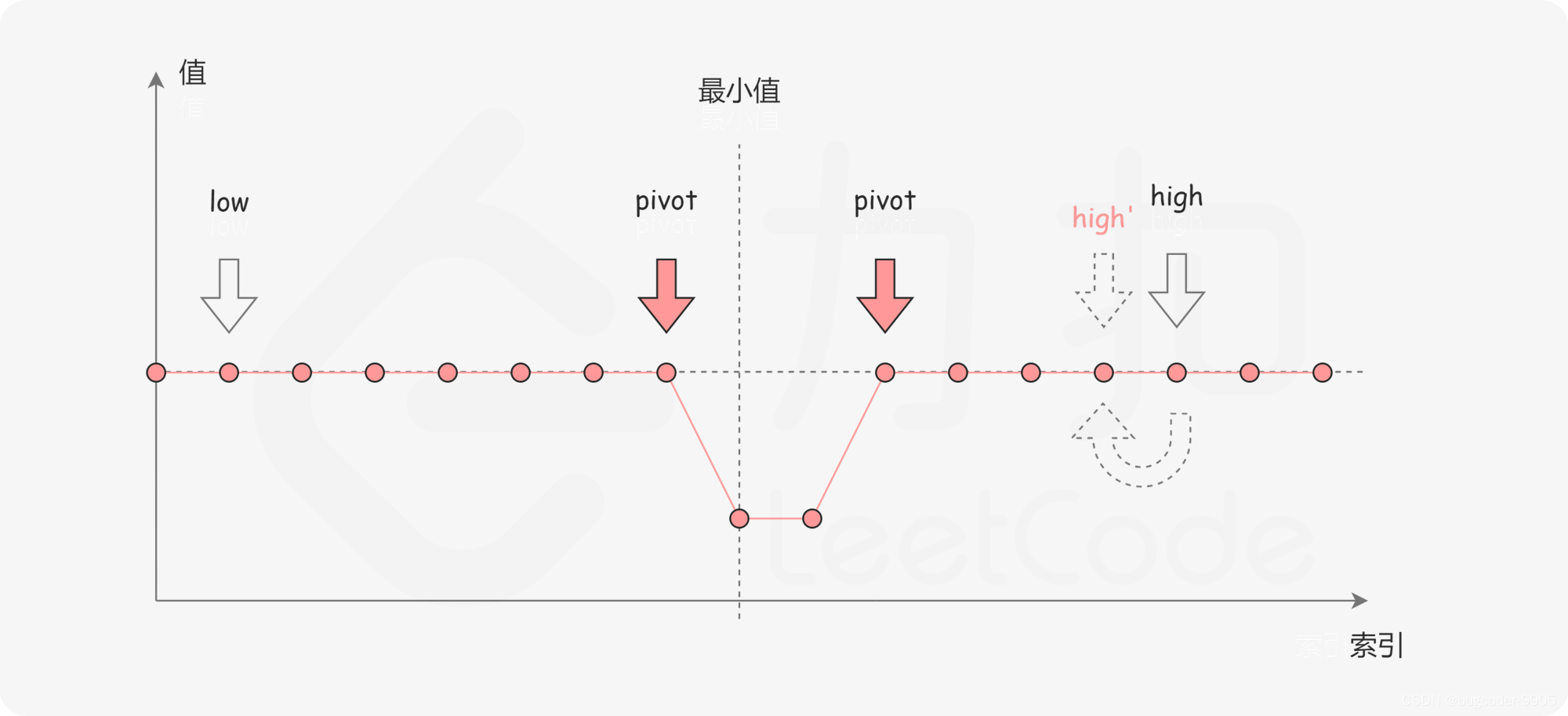
nums[mid] == nums[l],无法判断最小值在哪个区间,但一定在(l, r]内部
我们假设nums[l]、nums[mid]就是最小值,那我们可以排除l,即l++,因为nums[mid]可以替代nums[l]
若nums[l]、nums[mid]不是最小值,我们直接l++
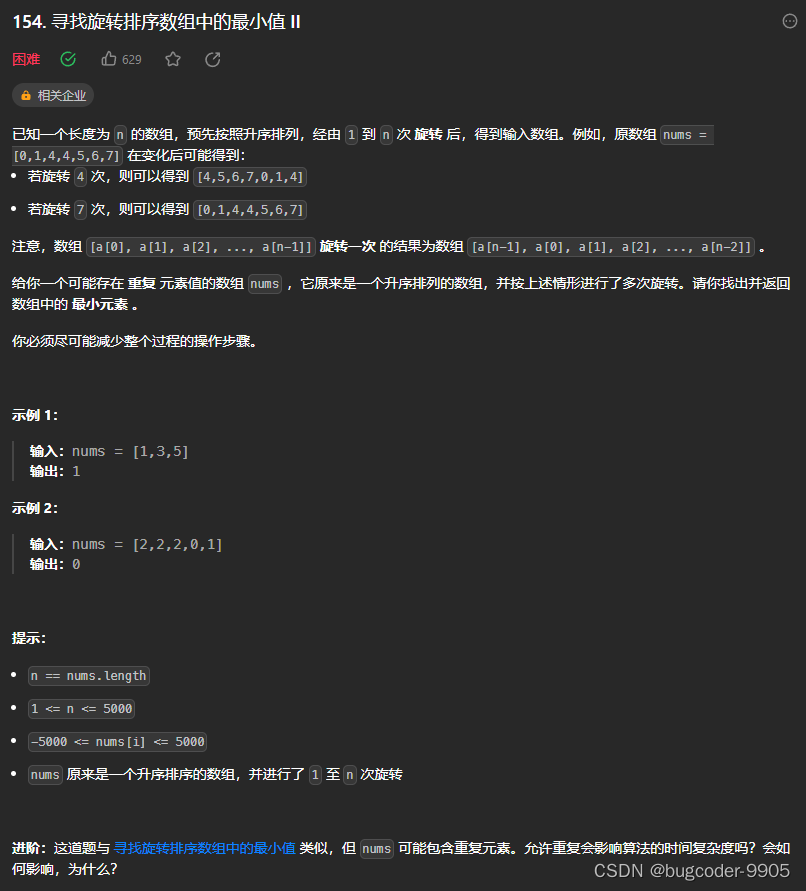
寻找旋转排序数组中的最小值 II
class Solution {
public int findMin(int[] nums) {
int n = nums.length;
int l = 0;
int r = n - 1;
while(l <= r){
if(l == r || nums[l] <= nums[r]){
// [l,r]已经有序
break;
}
int mid = l + (r - l) / 2;
if(nums[mid] > nums[l]){
l = mid + 1;
}else if(nums[mid] < nums[l]){
r = mid;
}else{
l++;
}
}
return nums[l];
}
}
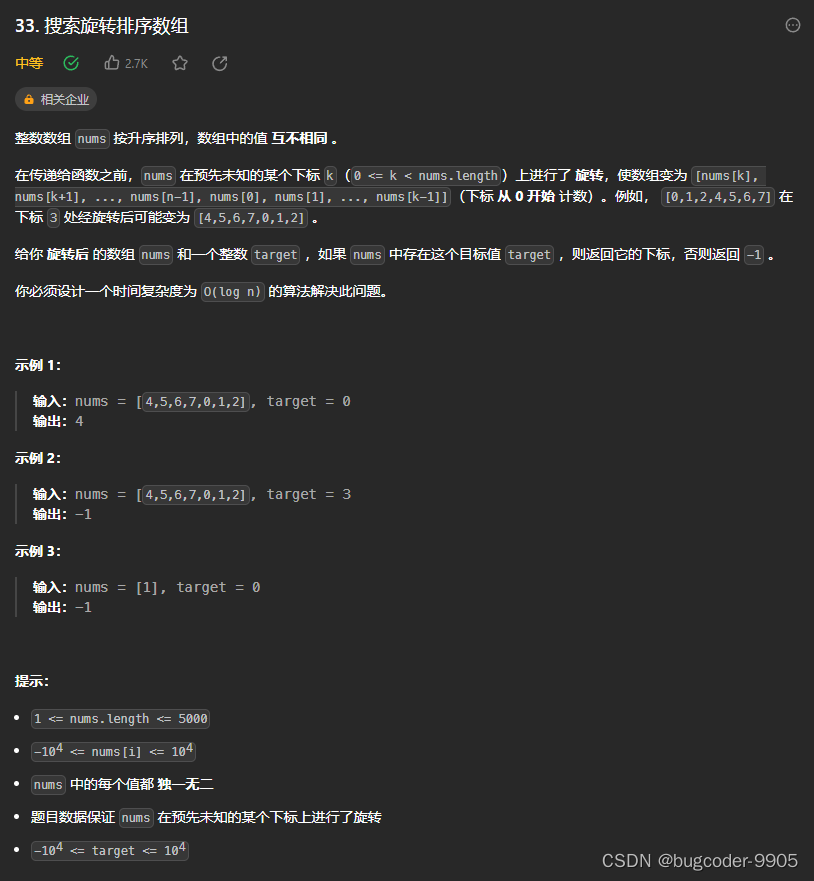
不重复数组找target,返回下标
class Solution {
public int search(int[] nums, int target) {
int n = nums.length;
int l = 0;
int r = n - 1;
while(l <= r){
int mid = l + (r - l) / 2;
if(target == nums[mid]){
return mid;
}
if(nums[mid] > nums[l]){
// [l, mid]有序
if(target >= nums[l] && target < nums[mid]){
// 在有序区间内
r = mid - 1;
}else{
l = mid + 1;
}
}else if(nums[mid] < nums[l]){
// [mid, r]有序
if(target > nums[mid] && target <= nums[r]){
// 在有序区间内
l = mid + 1;
}else{
r = mid - 1;
}
}else{
l++;
}
}
return -1;
}
}
重复数组找target,返回bool
class Solution {
public int search(int[] nums, int target) {
int n = nums.length;
int l = 0;
int r = n - 1;
while(l <= r){
int mid = l + (r - l) / 2;
if(target == nums[mid]){
return mid;
}
if(nums[mid] > nums[l]){
// [l, mid]有序
if(target >= nums[l] && target < nums[mid]){
// 在有序区间内
r = mid - 1;
}else{
l = mid + 1;
}
}else if(nums[mid] < nums[l]){
// [mid, r]有序
if(target > nums[mid] && target <= nums[r]){
// 在有序区间内
l = mid + 1;
}else{
r = mid - 1;
}
}else{
l++;
}
}
return -1;
}
}
重复数组找target,返回下标

class Solution {
public int search(int[] nums, int target) {
int l = 0;
int r = nums.length - 1;
if (r == -1)
return -1;
while (l < r) { // 循环结束条件l==r
int mid = l + (r - l) / 2;
if (nums[l] < nums[mid]) { // 如果左值小于中值,说明左边区间升序
if (nums[l] <= target && target <= nums[mid]) { // 如果目标在左边的升序区间中,右边界移动到mid
r = mid;
} else { // 否则目标在右半边,左边界移动到mid+1
l = mid + 1;
}
} else if (nums[l] > nums[mid]) { // 如果左值大于中值,说明左边不是升序,右半边升序
if (nums[l] <= target || target <= nums[mid]) { // 如果目标在左边,右边界移动到mid
r = mid;
} else { // 否则目标在右半边,左边界移动到mid+1
l = mid + 1;
}
} else if (nums[l] == nums[mid]) { // 如果左值等于中值,可能是已经找到了目标,也可能是遇到了重复值
if (nums[l] != target) { // 如果左值不等于目标,说明还没找到,需要逐一清理重复值。
l++;
} else { // 如果左值等于目标,说明已经找到最左边的目标值
r = l; // 将右边界移动到l,循环结束
}
}
}
return (nums[l] == target) ? l : -1; // 返回l,或者-1
}
}