栈和队列

1. 用两个栈实现队列

原题链接

补充：copy(a,b) 把a赋值给b

在这里插入图片描述

class MyQueue {
public:
    /** Initialize your data structure here. */
    stack<int> stk, cache;
    MyQueue() {

    }

    /** Push element x to the back of queue. */
    void push(int x) {
        stk.push(x);
    }

    void copy(stack<int> &a, stack<int> &b) {
        while (a.size()) {
            b.push(a.top());
            a.pop();
        }
    }

    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        copy(stk, cache);
        int res = cache.top();
        cache.pop();
        copy(cache, stk);
        return res;
    }

    /** Get the front element. */
    int peek() {
        copy(stk, cache);
        int res = cache.top();
        copy(cache, stk);
        return res;
    }

    /** Returns whether the queue is empty. */
    bool empty() {
        return stk.empty();
    }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * bool param_4 = obj.empty();
 */

class MyQueue {

    Stack<Integer> inStack;
    Stack<Integer> outStack;
    /** Initialize your data structure here. */
    public MyQueue() {
        inStack = new Stack<>();
        outStack = new Stack<>();
    }

    /** Push element x to the back of queue. */
    public void push(int x) {
        inStack.push(x);
    }

    /** Removes the element from in front of queue and returns that element. */
    public int pop() {
        while(!inStack.isEmpty()){
            outStack.push(inStack.pop());
        }
        int tmp = outStack.pop();
        while(!outStack.isEmpty()){
            inStack.push(outStack.pop());
        }
        return tmp;
    }

    /** Get the front element. */
    public int peek() {
        while(!inStack.isEmpty()){
            outStack.push(inStack.pop());
        }
        int res = outStack.peek();
        while(!outStack.isEmpty()){
            inStack.push(outStack.pop());
        }
        return res;
    }

    /** Returns whether the queue is empty. */
    public boolean empty() {
        return inStack.isEmpty() && outStack.isEmpty();
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

2. 包含min函数的栈

原题链接
在这里插入图片描述
本题我们用样例说话

比如是 1 2 3 4 5
那么对应的最小栈就是 1
如果是 5 4 3 2 1
对应就是 5 4 3 2 1
如果是 3 1 2 4 5
对应是 3 1

所以我们创建一个最小栈
如果入栈的值小于栈顶的值
就入最小栈

否则只入栈，不入最小栈

当最小栈和普通栈的栈顶一样时出栈

class MinStack {
public:
    /** initialize your data structure here. */
    stack<int> stackValue;
    stack<int> stackMin;
    MinStack() {

    }

    void push(int x) {
        stackValue.push(x);
        if (stackMin.empty() || stackMin.top() >= x)
            stackMin.push(x);
    }

    void pop() {
        if (stackMin.top() == stackValue.top()) stackMin.pop();
        stackValue.pop();
    }

    int top() {
        return stackValue.top();
    }

    int getMin() {
        return stackMin.top();
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

3. 栈的压入、弹出序列

原题链接

在这里插入图片描述

class Solution {
public:
    bool isPopOrder(vector<int> pushV,vector<int> popV) {
        if(popV.size() != pushV.size())
        {
            return false;
        }
        if(pushV.size()==0 && popV.size()==0)
            return true;
        stack<int> st;
        for(int i = 0,j = 0; i < popV.size(); i++)
        {
            if(popV[j]!=pushV[i])
            {
                st.push(pushV[i]);
            }
            else
            {
                st.push(pushV[i]);
                while(st.size() && j < popV.size() && st.top() == popV[j])
                {
                    st.pop();
                    j++;
                }
            }
        }
        if(st.size()==0)
            return true;
        return false;
    }
};

class Solution {
    public boolean isPopOrder(int [] pushV,int [] popV) {
        // 如果两个数组为空， 直接返回true， 两个数组长度不等， 返回false
        if(pushV == null && popV == null){
            return true;
        }
        if(pushV.length != popV.length){
            return false;
        }
        // 新建一个栈， 将push一个一个放入， 并判断
        // 如果元素与popV的top元素相等， 则弹出popV， 否则继续在stack里放元素
        // 如果顺序正确的话， PopV应该会为空值
        Stack<Integer> stack = new Stack<>();
        int index = 0;
        for(int i = 0; i< popV.length; i++){
            stack.push(pushV[i]);
            while(!stack.isEmpty() && stack.peek() == popV[index]){
                stack.pop();
                index++;
            }
        }
        return stack.isEmpty();
    }
}

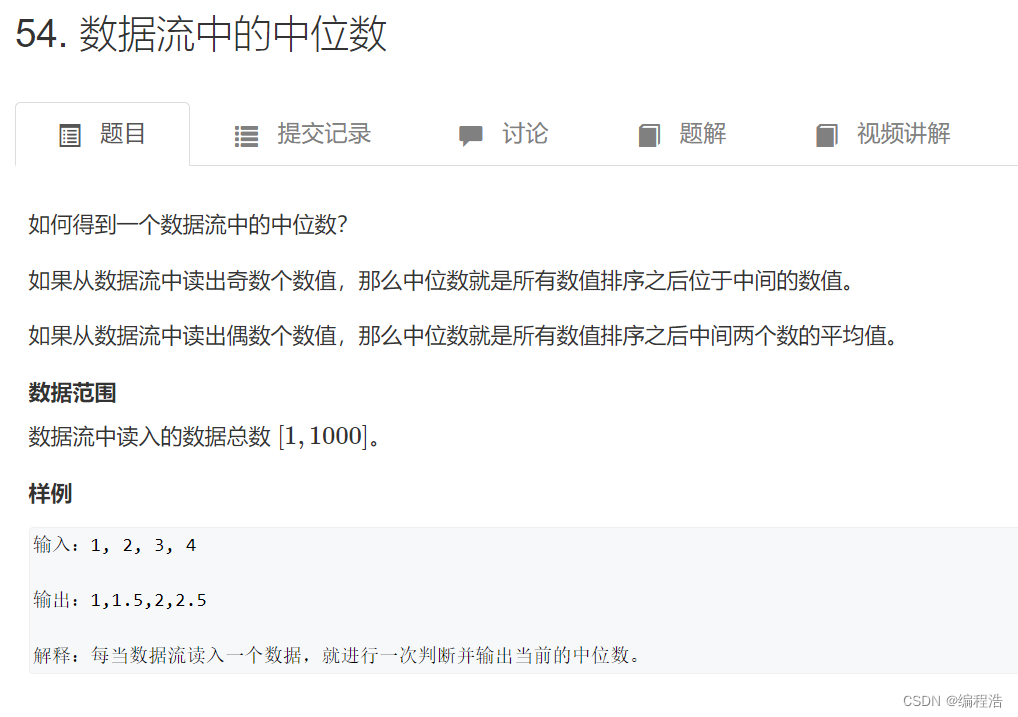
4. 数据流中的中位数（大根堆 + 小根堆）

原题链接

在这里插入图片描述

class Solution {
public:

    priority_queue<int> maxheap;
    priority_queue<int, vector<int>, greater<int> > minheap;

    void insert(int x){
        maxheap.push(x);
        if(minheap.size() && maxheap.top() > minheap.top())  // **1
        {
            int maxe = maxheap.top(), mine = minheap.top();
            maxheap.pop(), minheap.pop();
            maxheap.push(mine), minheap.push(maxe);
        }

        if(maxheap.size() > minheap.size() + 1)
        {
            minheap.push(maxheap.top());
            maxheap.pop();
        }
    }

    double getMedian(){
        if((maxheap.size() + minheap.size()) & 1) return maxheap.top();
        else return (maxheap.top() + minheap.top()) / 2.0;
    }
};

//这里填你的代码^^
//注意代码要放在两组三个点之间，才可以正确显示代码高亮哦~
/*
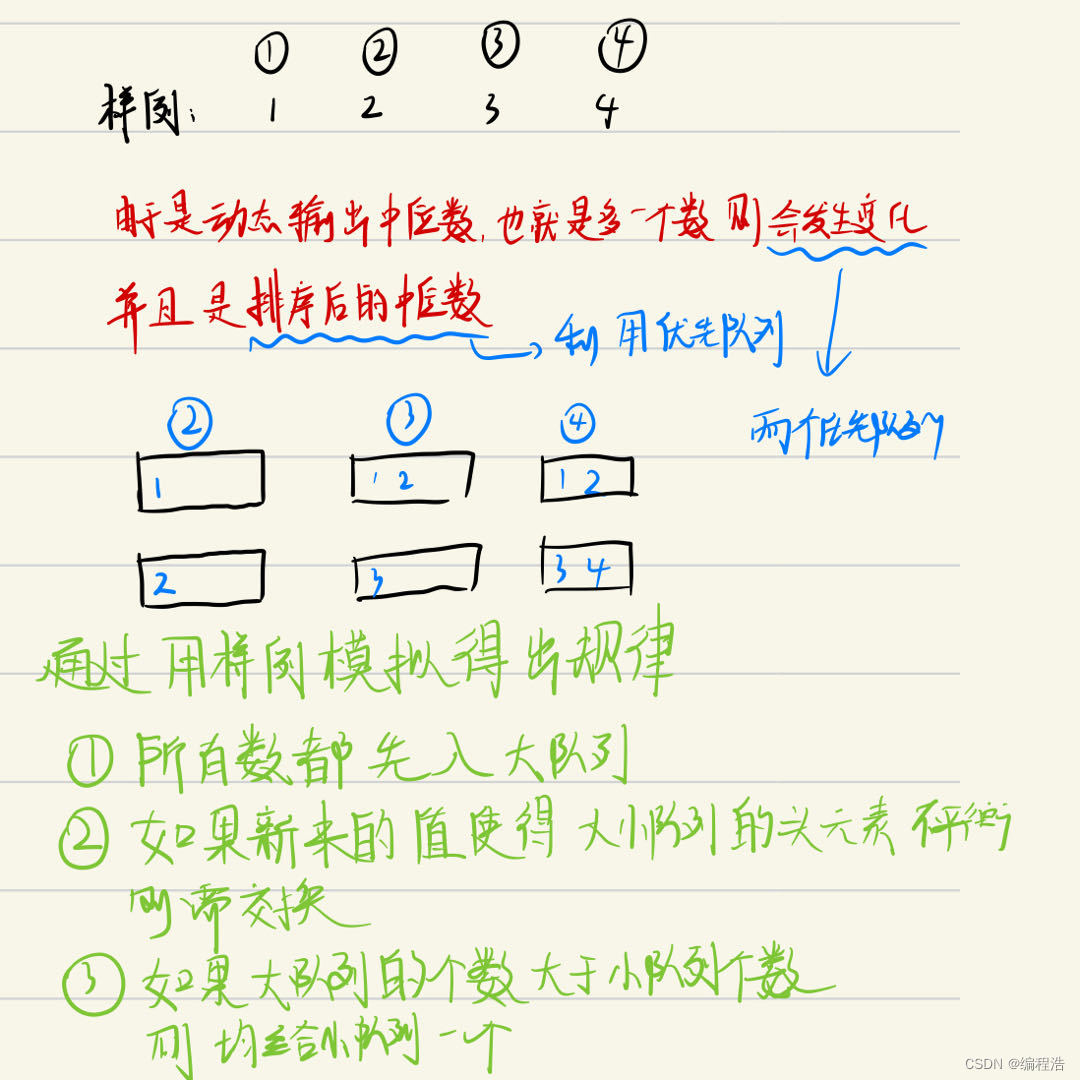
    最大堆保存左半部分，即较小一半
    最小堆保存右半部分，即较大一半
    但是新插入数据可能会比最大堆中最大的数字要小，
    也可能会比最小堆中最小的数字要大，
    因此先将数字放入最大堆，然后将最大堆中最大的数字放入最小堆
    （也可先将数字放入最小堆，然后将最小堆中最小的数字放入最大堆）
    这样始终保持，最大堆中最大的数字，比最小堆最小的数字还要小。
    同时控制数字数量，保证最大堆的容量与最小堆的容量差距不超过1
    这样最终如果最大堆的容量较大，则直接返回最大堆顶，
    否则两个堆顶数字相加除以2.0（返回double）
*/
class Solution {

    Queue<Integer> maxHeap = new PriorityQueue<>((a,b)->b-a);
    Queue<Integer> minHeap = new PriorityQueue<>();
    public void insert(Integer num) {
        maxHeap.add(num);
        minHeap.add(maxHeap.poll());
        if(maxHeap.size() < minHeap.size()){
            maxHeap.add(minHeap.poll());
        }
    }

    public Double getMedian() {
        return maxHeap.size() > minHeap.size() 
               ? maxHeap.peek()
               : (maxHeap.peek() + minHeap.peek()) / 2.0;
    }

}

5. 圆圈中最后剩下的数字【全部入队列】

原题链接
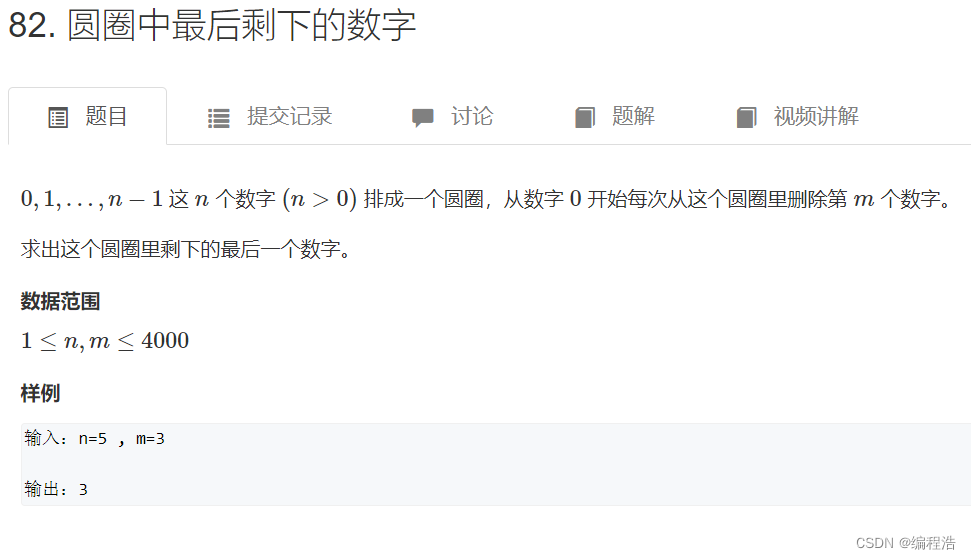
在这里插入图片描述
直接维护一个队列来做：
每走过一步，就把队首元素放到队列的后面，每走完m步把队列头元素删除
直到进行完n-1次迭代

class Solution {
public:
    int lastRemaining(int n, int m){
        queue<int> q;
        for(int i = 0;i < n; i++) q.push(i);
        int cnt = 0;
        int s = q.size();
        while(cnt < n - 1){
        int curr = 0;//curr表示当前走了多少步
           while(curr < m - 1){ //每次从0开始走m-1步
               int t = q.front();
               q.pop();
               q.push(t);
               curr ++;
           }//循环结束说明当前走到了第m个元素
           q.pop();//把第m个元素删掉
           cnt ++;
        }

        return q.front();//删完n-1个元素，队列里剩下的就是最后一个元素，返回它
    }
};