sortedSet
sortedSet是Redis提供的一个非常特别的数据结构,常用作排行榜等功能,将用户id作为value,关注时间或者分数作为score进行排序。
与其他数据结构相似,zset也有两种不同的实现,分别是zipList和(hash+skipList)。
编码转换规则
规则如下:
zipList满足以下两个条件
- [score,value]键值对数量少于128个;
- 每个元素的长度小于64字节;
不满足以上两个条件时使用hash+skipList
- hash用来存储value到score的映射,这样就可以在O(1)时间内找到value对应的分数;
skipList按照从小到大的顺序存储分数
- skipList每个元素的值都是[value,socre]对
- hash保证快速查找和唯一 skiplist保证有序
每个跳表的节点也都会维护着一个score值,这个值在跳表中是按照从小到大的顺序排列好的。

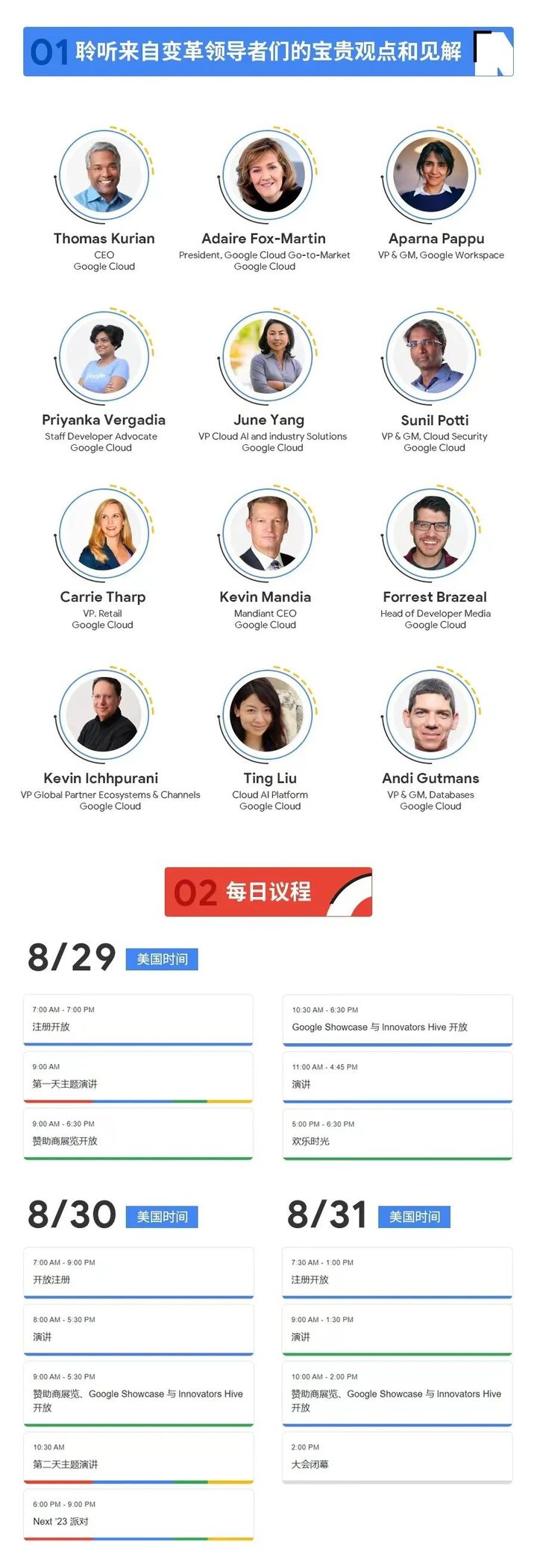
压缩列表
ziplist编码的压缩列表对象使用压缩列表作为底层实现,每个集合元素使用两个紧挨在一起的压缩列表节点来保存,第一个节点保存元素的成员(member),而第二个元素则保存元素的分值(score),压缩列表内的集合元素按分值从小到大进行排序,分值较小的元素被放置在靠近表头的方向,而分值较大的元素则被放置在靠近表尾的方向。
zipList结构如下:
指针指向的压缩列表表示如下:

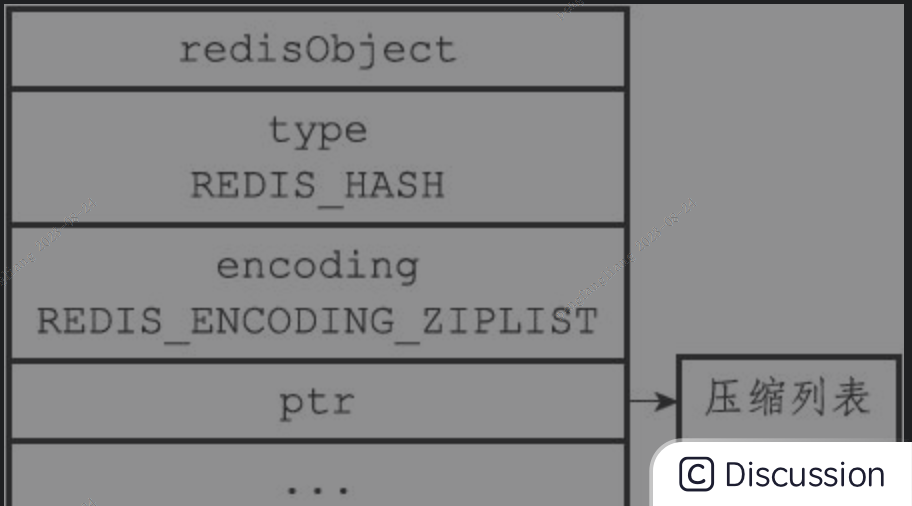
跳表
skiplist编码的有序集合对象使用zset结构作为底层实现,一个zset结构同时包含一个字典和一个跳跃表。 结构如下:

- zset结构中的zsl跳跃表按分值从小到大保存了所有集合元素,每个跳跃表节点都保存了一个集合元素:跳跃表节点的object属性保存了元素的成员,而跳跃表节点的score属性则保存了元素的分值。通过这个跳跃表,程序可以对有序集合进行范围型操作,比如ZRANK、ZRANGE等命令就是基于跳跃表API来实现的
- zset结构中的dict字典为有序集合创建了一个从成员到分值的映射,字典中的每个键值对都保存了一个集合元素:字典的键保存了元素的成员,而字典的值则保存了元素的分值。通过这个字典,程序可以用O(1)复杂度查找给定成员的分值,ZSCORE命令就是根据这一特性实现的
有序集合每个元素的成员都是一个字符串对象,而每个元素的分值都是一个double类型的浮点数。值得一提的是,虽然zset结构同时使用跳跃表和字典来保存有序集合元素,但这两种数据结构都会通过指针来共享相同元素的成员和分值,所以同时使用跳跃表和字典来保存集合元素不会产生任何重复成员或者分值,也不会因此而浪费额外的内存
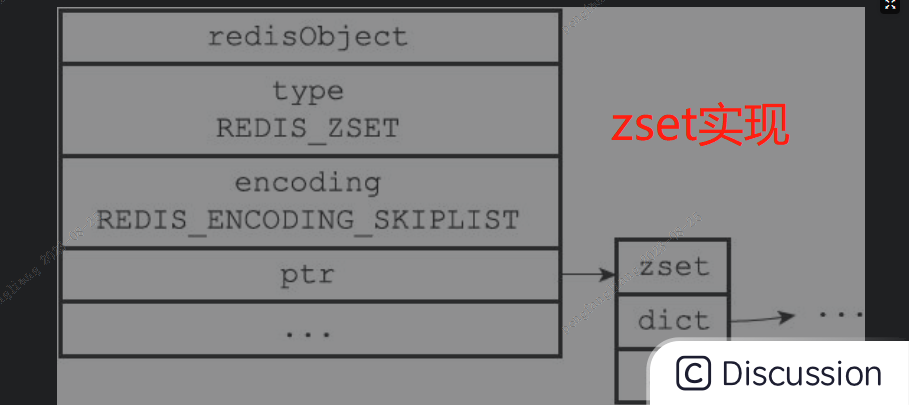
其具体实现方式如下:
字典保证速度,跳表保证顺序
有序集合可以单独使用字典或者跳跃表的其中一种数据结构来实现,但无论单独使用字典还是跳跃表,在性能上对比起同时使用字典和跳跃表都会有所降低
- 如果我们只使用字典来实现有序集合,那么虽然以O(1)复杂度查找成员的分值这一特性会被保留,但是,因为字典以无序的方式来保存集合元素,所以每次在执行范围型操作——比如ZRANK、ZRANGE等命令时,程序都需要对字典保存的所有元素进行排序,完成这种排序需要至少O(NlogN)时间复杂度,以及额外的O(N)内存空间(因为要创建一个数组来保存排序后的元素)
- 如果我们只使用跳跃表来实现有序集合,那么跳跃表执行范围型操作的所有优点都会被保留,但因为没有了字典,所以根据成员查找分值这一操作的复杂度将从O(1)上升为O(logN)
字典用于快速查找分值,跳跃表用于执行范围操作。
使用跳表时的示意图:
跳表skipList在Redis中的运用场景只有一个,那就是作为有序列表zset的底层实现。
跳表可以保证增、删、查等操作时的时间复杂度为O(logN),这个性能可以与平衡树相媲美,但实现方式上却更加简单,唯一美中不足的就是跳表占用的空间比较大,其实就是一种空间换时间的思想。跳表的结构如下所示:
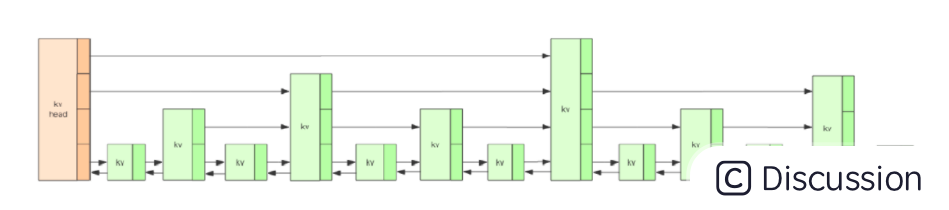
Redis中跳表一个节点最高可以达到64层,一个跳表中最多可以存储2^64个元素。跳表中,每个节点都是一个skiplistNode,每个跳表的节点也都会维护着一个score值,这个值在跳表中是按照从小到大的顺序排列好的。
跳表的结构定义如下所示:
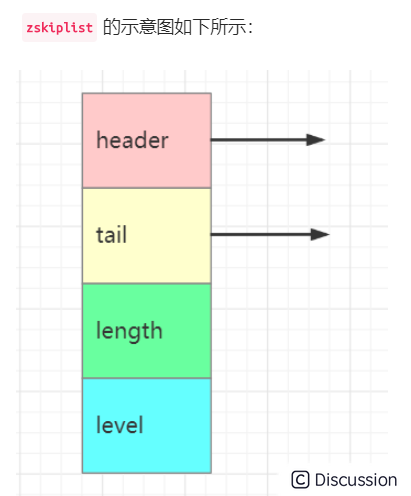
header:指向跳表的头节点,通过这个指针可以直接找到表头,时间复杂度为O(1);
tail:指向跳表的尾节点,通过这个指针可以直接找到表尾,时间复杂度为o(1);
length:记录跳表的长度,即不包括头节点,整个跳表中有多少个元素;
level:记录当前跳表内,所有节点中层数最大的level;
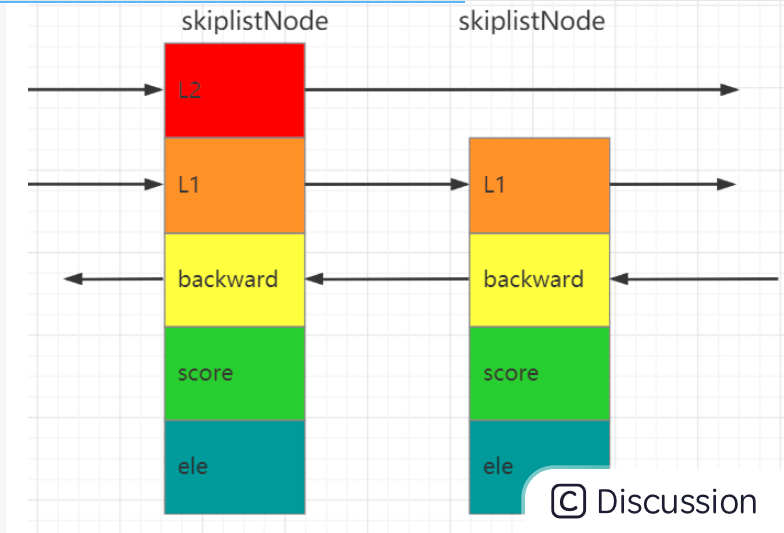
zskiplistNode的结构定义如下:
typedf struct zskiplistNode{ sds ele;// 具体的数据 double score;// 分数 struct zskiplistNode *backward;//后退指针 struct zskiplistLevel{ struct zskiplistNode *forward;//前进指针forward unsigned int span;//跨度span }level[];//层级数组 最大32 }zskiplistNode;
ele:真正的数据,每个节点的数据都是唯一的,但节点的分数score可以是一样的。两个相同分数score的节点是按照元素的字典序进行排列的;
score:各个节点中的数字是节点所保存的分数score,在跳表中,节点按照各自所保存的分数从小到大排列;
backward:用于从表尾向表头遍历,每个节点只有一个后退指针,即每次只能后退一步;
层级数组:这个数组中的每个节点都有两个属性,forward指向下一个节点,span跨度用来计算当前节点在跳表中的一个排名,这就为zset提供了一个查看排名的方法。
数组中的每个节点中用1、2、3等字样标记节点的各个层,L1代表第一层,L2代表第二层,L3代表第三层;,以此类推;
skiplistNode的示意图如下所示:
以下图为例,讲解一下skiplist的增删改查过程。
跳表范围查询
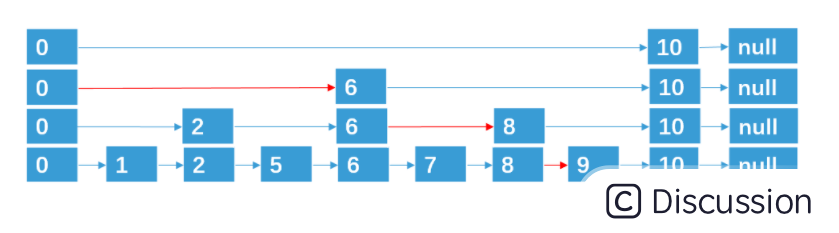
假设现在要查找9这个节点,步骤如下:
- 从head开始遍历,指针指向10这个节点,由于9<10,且同层的下一个指针指向NULL,所以层级数组要下降一层;
- 跳到6节点所在的层,同理,6<9,且同层的下一个指针指向10,再下降一层;
- 跳到8节点所在的层,同理,8<9,且同层的下一个指针指向10,再下降一层;
- 此时到了第一层,第一层是一个双向链表,由于8<9,所以开始向后遍历,查找到9就返回,不然就返回NULL;
跳表精准查询:hash
根据key在hash表直接找,时间复杂度O(1)。
跳表添加
上面例子中,9个结点,一共4层,可以说是理想的跳跃表了,不过随着我们对跳跃表进行插入/删除结点的操作,那么跳跃表结点数就会改变,意味着跳跃表的层数也会动态改变。
这里我们面临一个问题,就是新插入的结点应该跨越多少层?
这个问题已经有大牛替我们解决好了,采取的策略是通过抛硬币来决定新插入结点跨越的层数:每次我们要插入一个结点的时候,就来抛硬币,如果抛出来的是正面,则继续抛,直到出现负面为止,统计这个过程中出现正面的次数,这个次数作为结点跨越的层数。
通过这种方法,可以尽可能着接近理想的层数。大家可以想一下为啥会这样呢?
插入
例如,我们要插入结点 3,4,通过抛硬币知道3,4跨越的层数分别为 0,2 (层数从0开始算),则插入的过程如下:
插入 3,跨越0层。
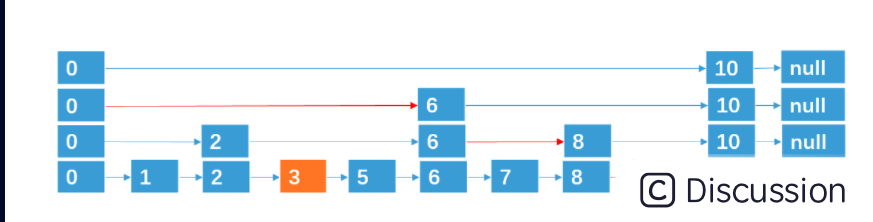
插入 4,跨越2层。
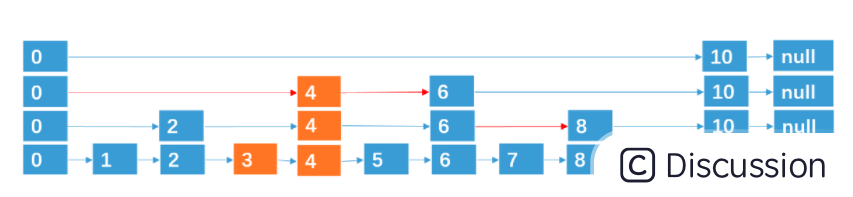
- 从 head 节点开始,先是在 head 开始降层来查找到最后一个比 4小的节点;
- 等到查到最后一个比 4 小的节点的时候(假设为3 );
- 然后需要引入一个随机层数算法来为这个节点随机地建立层数;
- 把这个节点插入进去以后,同时更新一遍最高的层数即可;
``` int zslRandomLevel(void) { int level = 1; while ((random()&0xFFFF) < (ZSKIPLISTP * 0xFFFF)) level += 1; return (level MAXLEVEL) ? level : ZSKIPLIST MAXLEVEL; } #define ZSKIPLISTMAXLEVEL 32
define ZSKIPLIST_P 0.25
```
跳表删除
删除的过程前期与查找相似,先定位到元素所在的位置,再进行删除,最后更新一下指针、更新一下最高的层数。
解决了插入之后,我们来看看删除,删除就比较简单了,例如我们要删除4,那我们直接把4及其所跨越的层数删除就行了。
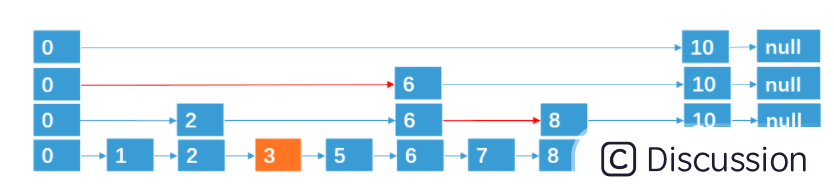
跳表修改
先是判断这个 value 是否存在,如果存在就是更新的过程,如果不存在就是插入过程。在更新的过程是,如果找到了Value,先删除掉,再新增,这样的弊端是会做两次的搜索,在性能上来讲就比较慢了,在 Redis 5.0 版本中,Redis 的作者 Antirez 优化了这个更新的过程,目前的更新过程是如果判断这个 value是否存在,如果存在的话就直接更新,然后再调整整个跳跃表的 score 排序,这样就不需要两次的搜索过程。
跳跃表的插入与删除至此都讲完了,总结下跳跃表的有关性质:
(1). 跳跃表的每一层都是一条有序的链表.
(2). 跳跃表的查找次数近似于层数,时间复杂度为O(logn),插入、删除也为 O(logn)。
(3). 最底层的链表包含所有元素。
(4). 跳跃表是一种随机化的数据结构(通过抛硬币来决定层数)。
(5). 跳跃表的空间复杂度为 O(n)。
跳跃表 vs 二叉查找树
有人可能会说,也可以采用二叉查找树啊,因为查找查找树的插入、删除、查找也是近似 O(logn) 的时间复杂度。
不过,二叉查找树是有可能出现一种极端的情况的,就是如果插入的数据刚好一直有序,那么所有节点会偏向某一边。例如
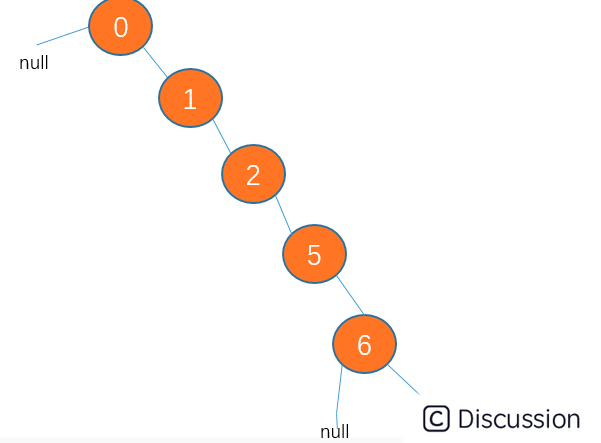
这种接结构会导致二叉查找树的查找效率变为 O(n),这会使二叉查找树大打折扣。
跳跃表 vs 红黑树
红黑可以说是二叉查找树的一种变形,红黑在查找,插入,删除也是近似O(logn)的时间复杂度,但学过红黑树的都知道,红黑树比跳跃表复杂多了,反正我是被红黑树虐过。在选择一种数据结构时,有时候也是需要考虑学习成本的。
红黑树插入,删除结点时,是通过调整结构来保持红黑树的平衡,比起跳跃表直接通过一个随机数来决定跨越几层,在时间复杂度的花销上是要高于跳跃表的。
当然,红黑树并不是一定比跳跃表差,在有些场合红黑树会是更好的选择,所以选择一种数据结构,关键还得看场合。
总上所述,维护一组有序的集合,并且希望在查找、插入、删除等操作上尽可能快,那么跳跃表会是不错的选择。
redis 中的数据数据便是采用了跳跃表,当然,ridis也结合了哈希表等数据结构,采用的是一种复合数据结构。
跳表 VS B+树
因为B+树的原理是 叶子节点存储数据,非叶子节点存储索引,B+树的每个节点可以存储多个关键字,它将节点大小设置为磁盘页的大小,充分利用了磁盘预读的功能。
每次读取磁盘页时就会读取一整个节点,每个叶子节点还有指向前后节点的指针,为的是最大限度的降低磁盘的IO;因为数据在内存中读取耗费的时间是从磁盘的IO读取的百万分之一
而Redis是 内存中读取数据,不涉及IO,因此使用了跳表;
redis使用跳表不用B+树的原因是:redis是内存数据库,而B+树纯粹是为了mysql这种IO数据库准备的。B+树的每个节点的数量都是一个mysql分区页的大小16K
sortedSet VS map
redis的sortedSet采用的是哈希表+跳表。
java的HashMap采用的是(数组+链表+红黑树)。
java的LinkedHashMap采用的是(数组+链表+红黑树) + 双向链表。
java的TreeMap采用的是红黑树。
LinkedHashMap保证了插入顺序的一致性,所以可以保证遍历顺序和存放顺序的一致性。
TreeMap由于元素插入的时候会根据key进行排序,所以并不能保证遍历顺序和存放顺序的一致性。
感觉sortedSet和java中的各种map没有可比性。原因在于sortedSet可以根据分数和key查找元素。而java中的各种map只能根据key找元素。
个人觉得如果java要模拟实现sortedSet,可以采用HashMap+TreeMap。

![java八股文面试[JVM]——JVM内存结构2](https://img-blog.csdnimg.cn/337de420415c4aa8b1347b5cd9dee5a3.png)




![【java】【项目实战】[外卖二]后台登录与退出功能实现](https://img-blog.csdnimg.cn/5732a7ac931642ceae5629630cb33359.png)