问题
图像拼接是图像处理的基础之一,虽然自己并没有直接做图像拼接方面的研究,但在面试中却多次被问到这方面的内容,可见这个知识点还是很重要的。事实上,很多场景都会用到图像拼接的知识,例如运动检测与跟踪、游戏画面的重建等。
本文参考自公众号“计算机视觉life”(一个很不错的CV相关的公众号,有兴趣可以关注关注)关于退昂拼接的一篇文章https://mp.weixin.qq.com/s/sHv-VOnn9WHQvq4hPOLgrA。这里主要关注在图像拼接的原理部分,所以对部分内容稍作删减和补充,主要介绍计算单应性矩阵H以及图像变形和融合。
图像拼接介绍
图像拼接(image mosaic)是将同一场景中的两张或多张重叠图像拼接成一张更大图像的技术,在机器视觉、医学成像等多个领域有着广泛的应用。常见的图像拼接算法流程如下:
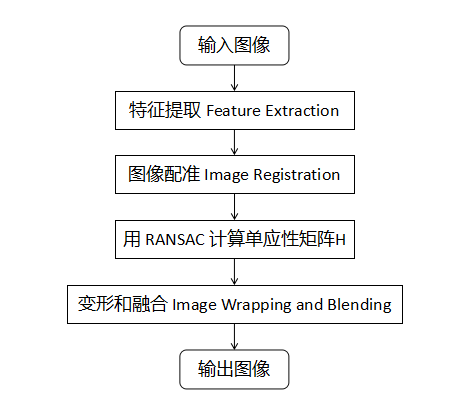
下面简单梳理一下上面步骤中涉及到的一些基本概念:
● 特征提取: 即提取输入图像中的特征,例如角点、边缘等信息。
● 图像配准: 即将同一目标场景下的两张或多张图像在空间位置上对准。
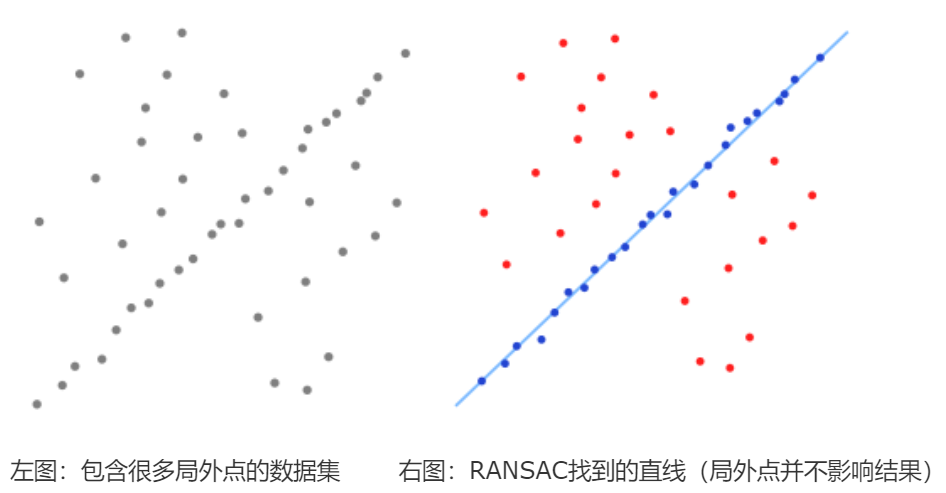
● RANSAC: 随机抽样一致性算法,用来剔除异常值(误匹配点)。
● 单应性矩阵: 即同一场景中两幅图像的空间映射关系。
● 图像变形: 将其中一幅图像进行重投影(可由单应性矩阵实现),并将图像放置在更大的画布上(拼接在一起)。
● 图像融合: 处理拼接边界处的灰度,使两张图像拼接后平滑过渡。
1.特征提取(Feature Extraction)
特征提取的主要目的是为后面进行图像配准而服务的,因此特征提取算法也影响了图像配准的精度,常用的特征提取方法有:
● Harris角点检测算法
● SIFT关键点检测算法
● SURF角点检测算法
● FAST角点检测算法
对于上述特征提取算法,这里不展开介绍,应该大多有过图像相关经验的都对这部分内容有一定的了解,如果有兴趣了解可以继续阅读参考资料。
2.图像配准(Image Registration)
图像配准是指将两张图像的特征点对应匹配起来,常见的图像配准方法有:
● NCC算法: 归一化互相关(normalized cross correlation)
归一化互相关算法的原理是计算第一幅图像每个点在周围窗口内的像素与另一幅图像每个点周围窗口内的像素之间的相关性,也就是窗口的灰度信息相关性,依次来衡量两幅图局部特征的相似度。
这种算法原理简单,只是要计算第一幅图像中的每个点与另一幅图像中同一行的每个点的互相关信息,计算量很大,所以也比较慢。当然,这可以改进,而且在提取特征点之后不需要对图像的每个点都遍历,可以只关注特征点附近的信息。
● SSD算法: 差值平方和算法(sum of squared difference)
SSD算法和NCC思想差不多,都是局部的基于灰度信息的匹配算法,只不过在衡量相似性的方法上不同,NCC才用的是互相关信息,而SSD算法计算的是窗口内对应像素差值的平方和,其值越小相似性越高。
图像配准的方法还有很多,这里不作为重点介绍,了解即可,下面看看配准的效果图:

3.计算单应性矩阵H
在介绍如何估计单应性矩阵之前,需要先采用RANSAC算法进行单应。
随机抽样一致性算法RANSAC(random sample consensus)
RANSAC算法从可能含有异常值的观测数据中拟合数学模型,是一种通过迭代方式估计模型参数的方法。RANSAC是一种不确定算法,因为它只在一定的概率下产生一个合理的结果,若执行更多次的迭代,这个概率会增加。在存在大量可用数据分层的情况下,这个算法可以以鲁棒的方式拟合模型。RANSAC算法在计算机视觉中有许多应用。
● RANSAC的原理:
RANSAC算法在基于下面假设的情况下,通过迭代的方式,直到某个参数模型的局内点数目最大,则认为该模型为最优模型。
● RANSAC的基本假设:
① 数据集中的有效数据由“局内点”组成,可以估计模型参数
② “局外点”是不能满足该模型的数据(其产生的原因有:噪声的极值、错误的测量方法、对数据的错误假设等)
③ 其余的数据属于噪声
● RANSAC算法步骤:
- 随机选取N个数据(3个点对)
- 估计参数 x(计算单应变换矩阵H)
- 根于使用者设定的阈值,找到可用数据总数M中适合该模型向量 x 的数据对总数量 K( 计算每个匹配点经过单应变换矩阵后到对应匹配点的距离,根据预先设定的阈值将匹配点集合分为局内点和局外点,如果局内点足够多,则H足够合理,用所有内点重新估计H)。
- 如果符合的数量K足够大,则接受该模型并退出,一次迭代结束
- 重复1-4步骤 T次,退出
K有多大取决于我们认为属于合适结构的数据的百分比以及图像中有多少结构。如果存在多个结构,则在成功拟合后,删除拟合数据并重做RANSAC。
在执行RANSAC之后,我们只能在图像中看到正确的匹配,因为RANSAC找到了一个与大多数点相关的单应矩阵,并将不正确的匹配作为异常值丢弃。
单应性矩阵(Homography)
有了两组相关点(即匹配的特征点),接下来就需要建立两组点的转换关系,也就是图像变换关系。
● 单应性是两个空间之间的映射,常用于表示同一场景的两个图像之间的对应关系;
● 这种对应关系可以匹配大部分相关的特征点,并且能实现图像投影,使一张图通过投影和另一张图实现大面积的重合。
假设两张图像的匹配点分别是
X
=
[
x
,
y
]
T
X=[x,y]^{T}
X=[x,y]T 和
X
′
=
[
x
′
,
y
′
]
T
X'=[x',y']^{T}
X′=[x′,y′]T,则两者的关系必须满足:
X
′
=
H
X
X'=HX
X′=HX 。如果使用齐次坐标表示这两个匹配点,则上述关系可以表示为:
(
x
′
y
′
1
)
=
[
h
11
h
12
h
13
h
21
h
22
h
23
h
31
h
32
1
]
(
x
y
1
)
\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{bmatrix} h_{11} & h_{12} & h_{13}\\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & 1\end{bmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}
⎝⎛x′y′1⎠⎞=⎣⎡h11h21h31h12h22h32h13h231⎦⎤⎝⎛xy1⎠⎞
可见,单应性矩阵H是一个由8个参数组成的变换矩阵,因此,选取4对匹配点即可确定一个单应性矩阵H。
用RANSAC方法估算H:
- 首先进行特征提取,检测两个图像的角点。
- 采用NCC进行配准,收集相关性足够高的点对,形成一组候选匹配。
- 选择4个点,计算单应性矩阵 H。
- 选择与单应性一致的点配对,即计算由一幅图的匹配点经过H变换后与另一幅图原来的匹配点之间的距离,如果小于某个阈值: D i s t ( P H , Q ) < ε Dist(P_{H},Q)<ε Dist(PH,Q)<ε,则点对 ( P , Q ) (P,Q) (P,Q) 被认为与单应性H一致。
- 重复3/4步骤,直到足够多的点对满足 H。
- 使用找到的所有满足条件的点对,通过公式重新计算得到最终的 H。
得到两幅图像之间的单应性矩阵H之后,就可以将某一幅图像通过单应性变换重投影到另一幅图像的平面上,实现拼接了,也就是下面的图像变形和融合。
4.图像变形和融合
最后一步是将所有输入图像变形并融合到一个符合的输出图像中。基本上,我们可以简单地将所有输入的图像变形到一个平面上,这个平面名为复合全景平面。
图像变形的步骤:
- 首先计算每个输入图像的变形图像坐标范围,得到输出图像大小,可以很容易地通过映射每个源图像的四个角并且计算坐标 ( x , y ) (x,y) (x,y) 的最小值和最大值确定输出图像的大小。最后,需要计算指定参考图像原点相对于输出全景图的偏移量 x o f f s e t x_{offset} xoffset 和偏移量 y o f f s e t y_{offset} yoffset。
- 下一步是使用上面所述的反向变形,将每个输入图像的像素映射到参考图像定义的平面上,分别执行点的正向变形和反向变形。(这里没看到推文中有提前的说明,我也没搞懂)

图像融合:
由于相机在拍摄时可能曝光不同,在图像拼接缝合处会出现一定的明暗差异,所以在融合过程中需要对这部分进行处理。最简单的可用处理方式是使用羽化(feathering),它使用加权平均颜色值融合重叠的像素。我们通常使用 alpha 因子,通常称为 alpha 通道,它在中心像素处的值为1,在与边界像素线性递减后变为0。
图像融合结果:(右侧一小部分是原来图2拼接在图1后的结果)


补充
在图像拼接后,有时候可能会产生一些重影,例如:(这里直接给出拼接后的结果图)

出现重影可能的原因:
① 拍摄方式:相机在拍摄图像时,曝光等参数设置不同可能影响图像后续处理的结果。
② 拍摄时间差:不同的时间拍摄同一场景,两张图像的重叠区域可能会有所不同,哪怕区别很微小。
③ 拍摄视差:由于拍摄过程中存在视差,导致拍摄的图像重叠区域可能不能完全重合。
不管何种方式导致的两张图像重叠区域不同,都有可能使得最终拼接的结果出现重影。
**另外:**拍摄的图片必须要包含超过一定比例的重叠区域,当重叠区域过小时,图像会由于匹配的特征点对不足,而导致拼接失败。当重叠区域过大时,则需要多张图像进行拼接才能获取到更宽视野的图像。一般情况下,重叠区域占整幅图像的40%- -50%, 图像能够找到足够配准的特征点对。
参考资料
计算机视觉life公众号–图像拼接:https://mp.weixin.qq.com/s/sHv-VOnn9WHQvq4hPOLgrA
图像拼接处理 https://www.cnblogs.com/cenyan/p/12557065.html



![[附源码]Python计算机毕业设计高校篮球训练管理系统Django(程序+LW)](https://img-blog.csdnimg.cn/d2e2ab7e7c3546d8b73f15ac7db677e2.png)


![[计算机网络微课]第三章 数据链路层](https://img-blog.csdnimg.cn/img_convert/b7bdef9ec13795ae5d9ab6c1fdff377c.png)