目的
主要是处理一些不相交集合的合并问题,比如:求连通子图,求最小生成树的克鲁斯卡尔算法以及最近公共祖先(LCA)等
简单应用就是连通图,将元素进行合并,如果要优化路径的话可以利用数据压缩
三大步骤
1.初始化
2.查询
3.合并
1.初始化
首先我们将所有节点的父节点设置为自己
fa[i]=i :比如fa[i]=j——>代表i的父元素是j

2.查询
寻找i元素的祖先(寻找代表元素,也就是公共节点)
**结束条件:**节点祖先节点为本身

3.合并
找到两个节点的祖先,然后将i的祖先指向j的祖先完成合并

优化
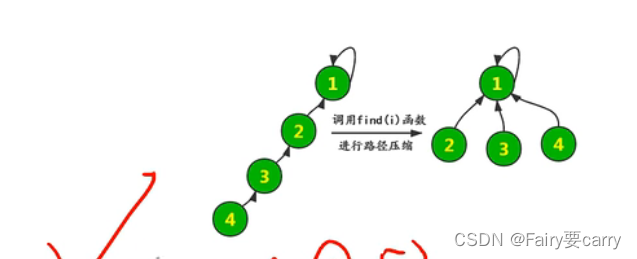
比如 union(4,6) ,4的父节点为3,3的父节点为2,这样递归下去,需要查询的次数太多
优化:路径压缩
比如 union(4,5),4的父节点为3,所以fa[4]=3,fa[3]=2,fa[2]=1,fa[1]=1为结束末尾条件
所以我们在find()方法中加一条语句进行路径压缩
int find(int i){
if(i==fa[i]){
return i;
}else{
fa[i]=find(fa[i]); //进行路径压缩
return fa[i]; //返回父节点
}
会发现链条发生转变,本质就是利用递归,调用父节点的父节点直至满足结束条件
实例
一开始有n伙山贼, 他们各自为营 但是他们都是有野心的
第3伙强盗 打下了第5伙强盗 第5伙强盗的老大就是第3伙强盗
然后第7伙强盗一看想要让第5伙强盗成为伙伴 打完第5伙还得打第3伙强盗
还不如直接打第3伙 于是第7伙强盗就打赢了第3伙强盗 然后第3伙和第5伙都归第7伙了
…
接下来就是各自纷争 然后最后看还剩下了几伙强盗 并且每一伙强盗都是谁
public class UnionFind {
private int[] id; 存储这几伙强盗的逻辑关系 数组下标i代表第i伙强盗 值代表 他老大是谁
private int count; 表示一共有几个强盗团伙
public UnionFind(int N) 做初始化操作 N 代表一开始有几伙强盗
public int getCount() 获取强盗团伙的数量
public boolean connected(int p, int q) 判断 p 和 q 这两伙强盗 是不是一家的
public int find(int p) 找到第p伙强盗的老大
public void union(int p, int q) 联合两伙强盗
}
1.构造方法
首先,大家肯定都是各自为营,所以说强盗团伙的数量 就等于强盗数量本身 所以 count = N
然后new出这N伙强盗的逻辑关系,长度就是一开始的强盗数量
最后一句话 大家各自为营 id[i] = i; 自己的老大就是自己
public UnionFind(int N) {
count = N;
id = new int[N];
for(int i = 0; i < N; i++) id[i] = i;
}
2.返回强盗数量
public int getCount() {
return count;
}
3.查找强盗的上级
public int find(int p) {
return id[p];
}
4.判断P和Q是否存在同一个上级
public boolean connected(int p, int q) {
return find(p) == find(q);
}
5.联合
将q作为p的老大,首先得到pq的老大,然后判断是否为同一个人,如果老大都一样说明都是一路人啥也不要做
否则p要被q干掉,从而q当p的老大——>遍历数组,只要发现第i路人马的老大就是p的老大,就让他们的老大变为q,记得最后团队-1
public void union(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot) return;
for(int i = 0; i < id.length; i++)
if(id[i] == pRoot) id[i] = qRoot;
count--;
}
优化
其他方法不用变 只需要 修改 find() 和 union的两个方法就可以 首先看一下 find()
public int find(int p) {
while(p != id[p]) p = id[p];
return p;
}
迭代遍历的是什么? 只要id[p]表示第p伙强盗的 老大
只要老大不是自己就寻找真正的老大
要注意这里你可以有点误区 因为其实我们的union() 方法也改了 这次做的并不是统一老大
上一个版本 我们3干掉了5 3就是5的老大 然后7干掉了3 3的老大和5的老大都变成了7
这次我们是3干掉了5 3就是5的老大 7干掉了3 3的老大是7 5的老大还是3
所以7是5的老大的老大
看一下 union()方法
public void union(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot) return;
id[pRoot] = qRoot;
count--;
}
这个就像一棵树,不像之前的把5的老大从6改为7,那么4的老大原本也是6就会收到影响也为7,因为6被7干掉了,强盗团队-1
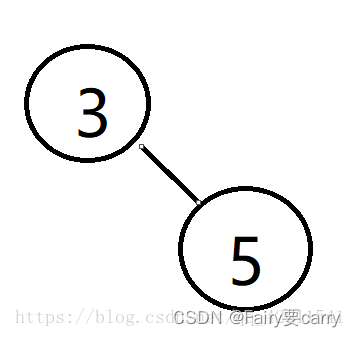
这里3干掉了5 就给3和5 连一条线 并且 ip[5] = 3;
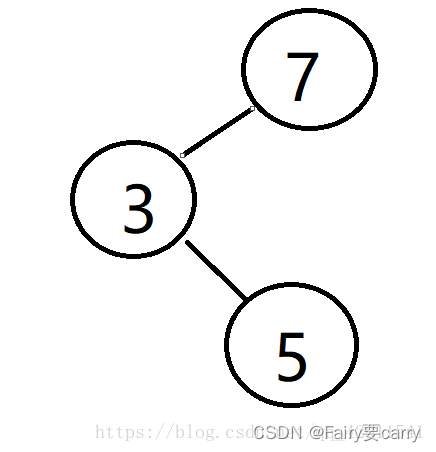
然后7干掉了3 就让3连向7 但是5还是连着3的 ip[3] = 7;
然后find查找5的时候 发现5的老大是3 然后p = 3 然后ip[3] != 3;说明 3还有老大 继续寻找3的老大
然后p=7; 发现7的老大就是7 所以出循环 并且返回7——>find()方法修改的意义,就是为了判断自己是否还有老大
这样的时间复杂度只取决于 这棵连接起来的树的高度
完整代码:
public class QuickUnion {
private int[] id;
private int count;
publicQuickUnion(int N) {
count = N;
id = new int[N];
for(int i = 0; i < N; i++) id[i] = i;
}
public int getCount() {
return count;
}
public boolean connected(int p, int q) {
return find(p) == find(q);
}
public int find(int p) {
while(p != id[p]) p = id[p];
return p;
}
public void union(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if(pRoot == qRoot) return;
id[pRoot] = qRoot;
count--;
}
}