题目：

 

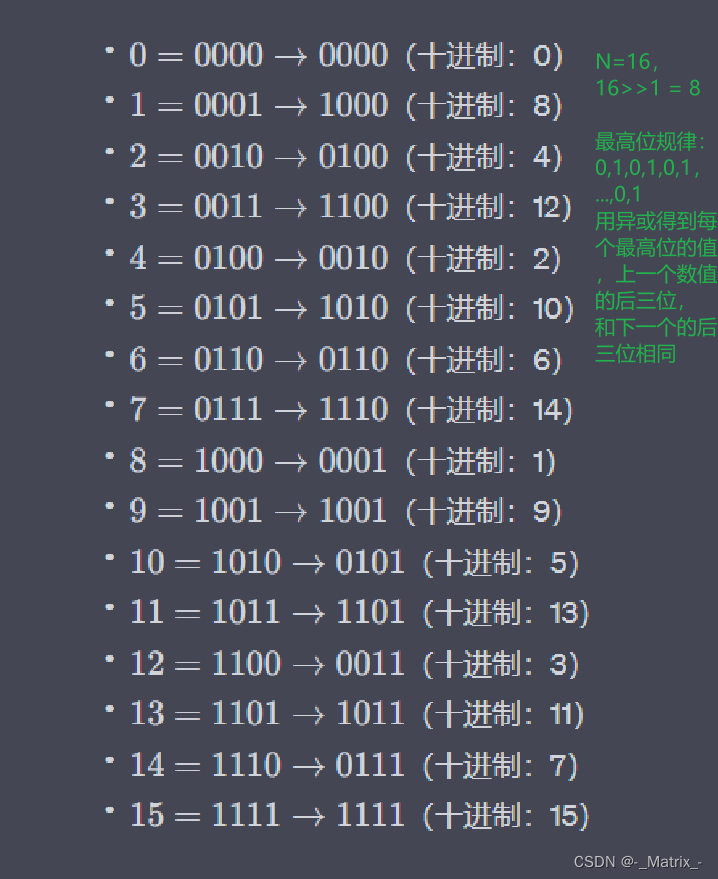
解题思路：看到题目的时候，一般第1反应是用两个循环暴力解题，时间复杂度是O(n^2)，不能通过，所以要优化，通过找规律。

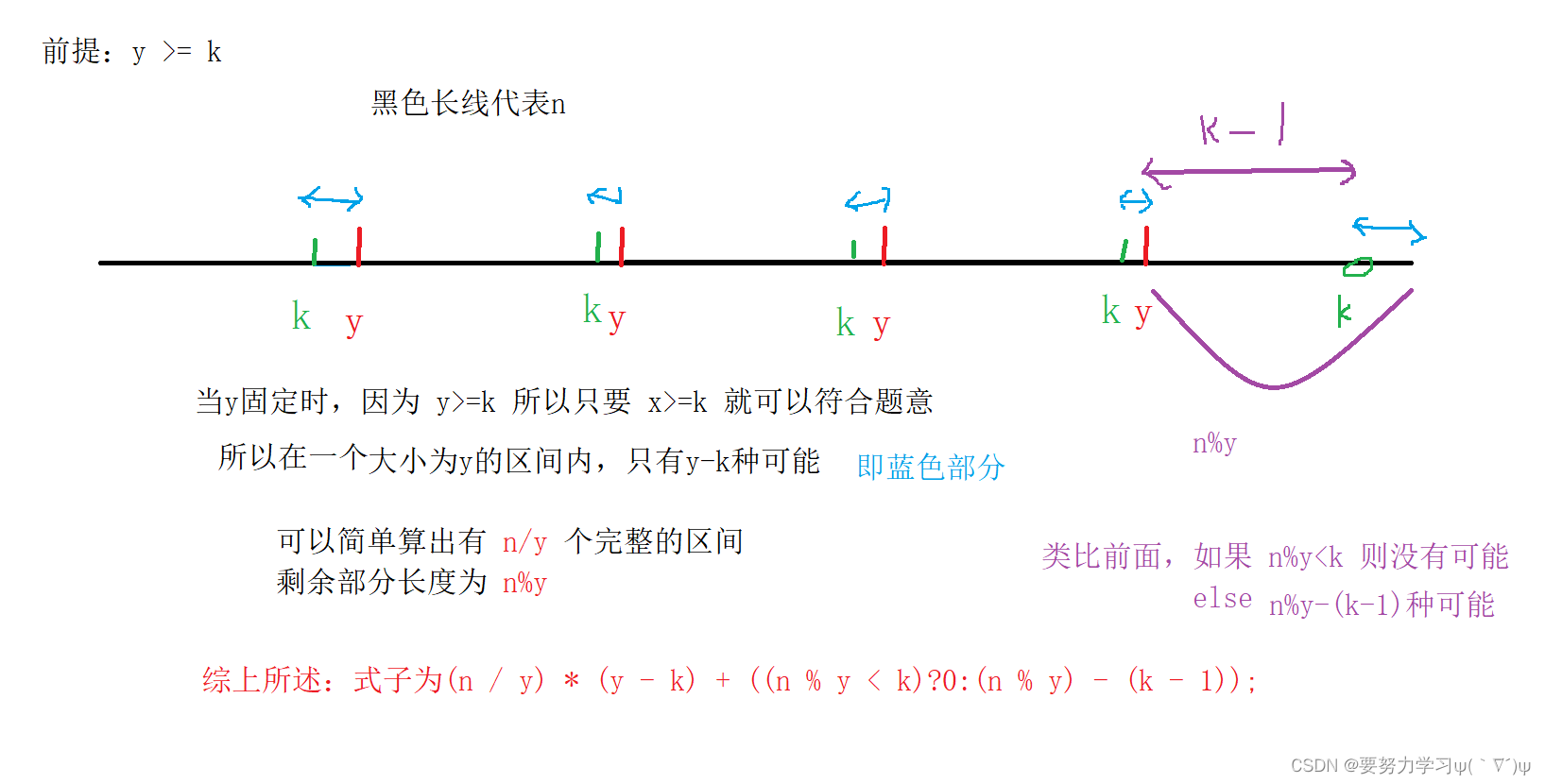
一、当 y <= k 时， 不可能符合题意，所以 y 从 k+1 开始遍历

(下面二、三是在y固定的情况下讨论)

二、当 x 属于区间 [0, y) 时，有 y-k 个可能的数对

三、可以算出有 n/y 个完整的区间，所以有(n / y) * (y - k) 个可能

四、看剩余区间，如果 n%y < k 则不可能有符合的情况，

                             如果前式大于等于k，有n%y-(k-1)个可能。

五、把所有可能加起来就是y固定时的所有情况，遍历y循环然后加起来就可以了。

        式子：(n / y) * (y - k) +((n%y < k)?0:n%y-(k-1));

详解： 

k==0时的讨论

 

 

#include <iostream>
using namespace std;

int main() {
    long long n = 0, k = 0;
    cin >> n >> k;
    long long count = 0;
    // if(k == 0)
    // {
    //     cout << n*n;
    //     return 0;
    // }
    //k == 0 上面下面两个都可以，上面的更简单
    if(k == 0)
    {
        for(int y = k+1; y <= n; ++y)
        {
        count += (n / y) * (y - k) + ((n % y < k)?0:(n % y) - k);
        }
        cout << count;
        return 0;
    }

    for(int y = k+1; y <= n; ++y)
    {
        count += (n / y) * (y - k) + ((n % y < k)?0:(n % y) - (k - 1));
    }
    cout << count;
    return 0;
}