蝴蝶翻转

实现一

在计算机科学和数字信号处理中，蝴蝶操作是一种常用于快速傅里叶变换（FFT）的操作。在蝴蝶算法中，输入数据的一部分通过特定的运算结构进行重新排列和组合，以便在计算FFT时实现高效处理。

蝴蝶操作的名称来自于它的结构图，其中输入和输出数据的排列方式看起来像蝴蝶的翅膀。

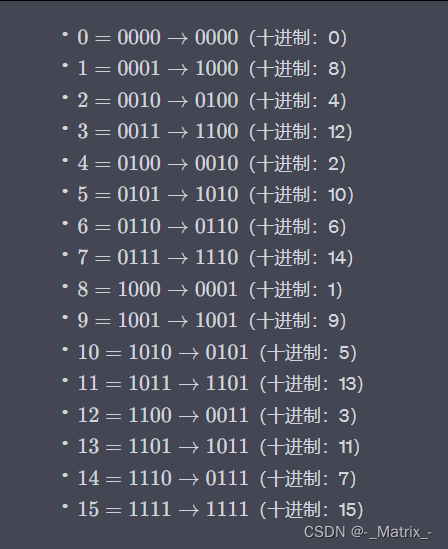
上图，对比每个数值的二进制，通过蝴蝶翻转，就得到了对应的数值。

2：

对0的第一位取反，得到1的蝴蝶数值，对0的前两位翻转得到3的蝴蝶值，对1的前两位翻转得到2的蝴蝶值。
对0的前三位翻转得到7的蝴蝶值，对1的前三位翻转得到6的蝴蝶值，对2的前三位翻转得到5的蝴蝶值，对3的前三位翻转得到4的蝴蝶值，…，以此类推。

代码实现：

//x 的大小必须是2的幂数，否则返回false  -- 改算法有个弊端需要维护x大小一样的数组
bool butterflyFlip(std::vector<std::complex<double>> & x)
{
	int N = x.size();

	//找到位数大小
	double bitNum = std::log2(N);
	//判断是否有小数，有小数说明N不是2的幂数
	if (bitNum != std::floor(bitNum))
	{
		return false;
	}
	std::vector<int> vec(N, 0);
	int backBit = N - 1;
	// 对每个数据进行蝴蝶翻转
	for (int i = 0; i < bitNum; ++i)
	{
		//当前最大索引
		int maxIndex = (2 << i) - 1;
		//当前最大索引一半
		int midIndex = 1 << i;

		//需要移动的位数
		int moveBit = bitNum - i - 1;
		for (int j = 0; j < midIndex; ++j)
		{
			//数据翻转
			vec[maxIndex - j] = ((~(vec.at(j) >> moveBit)) << moveBit) & backBit;

		}

	}

	//根据蝴蝶数组翻转数据
	for (int i = 0; i < N; ++i)
	{
		if (i < vec.at(i))
		{
			std::swap(x[i], x[vec.at(i)]);

		}
	}
	return true;
}

实现二

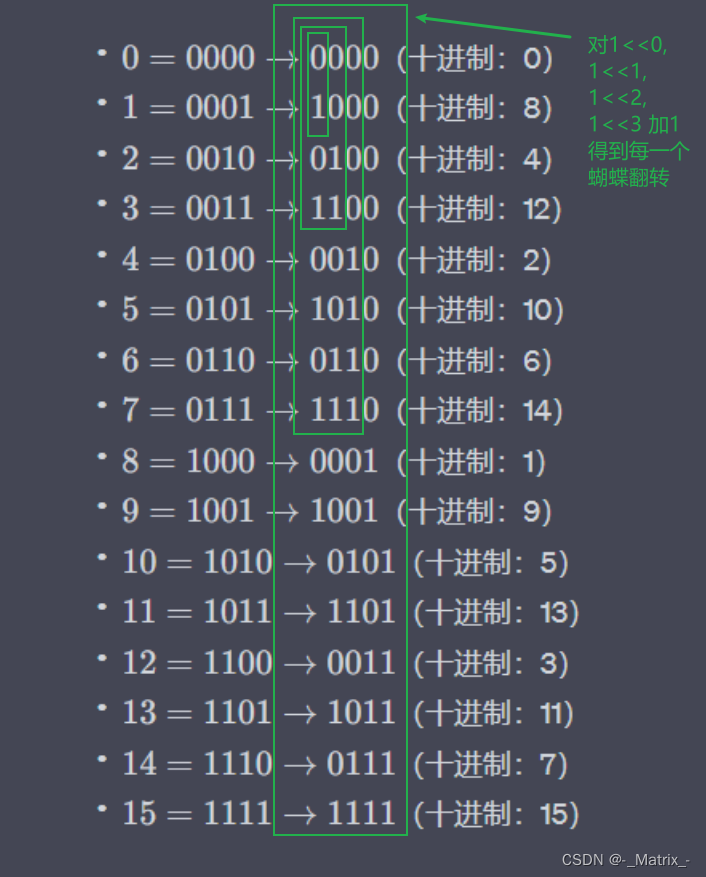
代码实现：

//x 的大小必须是2的幂数，否则返回false  -- 改算法有个弊端需要维护x大小一样的数组
bool butterflyFlip(std::vector<std::complex<double>> & x)
{
	int N = x.size();

	//找到位数大小
	double bitNum = std::log2(N);
	//判断是否有小数，有小数说明N不是2的幂数
	if (bitNum != std::floor(bitNum))
	{
		return false;
	}
	std::vector<int> vec(N, 0);
    // 对每个数据进行蝴蝶翻转
    for (int i = 0; i < bitNum; ++i)
    {
        //当前最大索引一半
        int midIndex = 1 << i;

        //需要移动的位数
        int moveBit = bitNum - i - 1;
        for (int j = 0; j < midIndex; ++j)
        {
            //数据翻转
            vec[j+midIndex] = (((vec.at(j) >> moveBit)+1) << moveBit);
        }

    }

	//根据蝴蝶数组翻转数据
	for (int i = 0; i < N; ++i)
	{
		if (i < vec.at(i))
		{
			std::swap(x[i], x[vec.at(i)]);

		}
	}
	return true;
}

实现三：

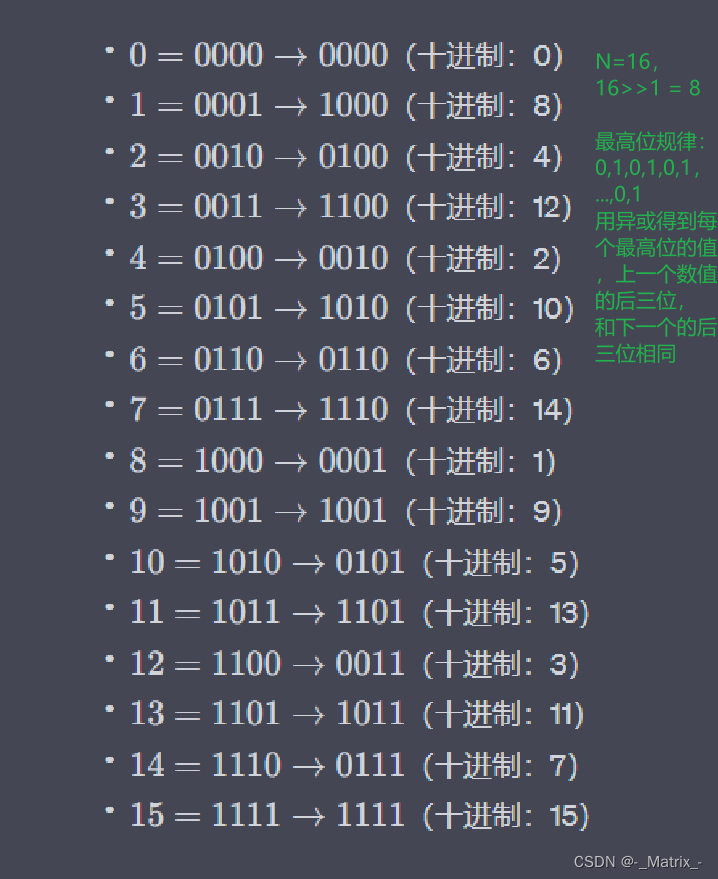
代码实现

//x 的大小必须是2的幂数，否则返回false 
bool butterflyFlip(std::vector<std::complex<double>> & x)
{
	int N = x.size();

	//找到位数大小
	double bitNum = std::log2(N);
	//判断是否有小数，有小数说明N不是2的幂数
	if (bitNum != std::floor(bitNum))
	{
		return false;
	}
	
	// 按位反转
	for (int i = 1, j = 0; i < N; i++)
	{
		//bit = N/2
		int bit = N >> 1;
		/*
		 * 我们正在查看j的二进制表示中的每一位。
			从左到右，我们检查每一位是否为1。
			对于每一个为1的位，我们将其反转为0。
			当我们遇到第一个为0的位时，循环终止。
		*/
		for (; j & bit; bit >>= 1)
		{
			j ^= bit;
		}
		//进行异或运算（XOR运算的工作原理是：当两个比较的位相同时，结果是0；当两个比较的位不同时，结果是1。）
		j ^= bit;

		//当 i >j 表示前面已经替换了位置， i==j,表示位置不用变
		if (i < j)
		{
			std::swap(x[i], x[j]);
		}
	}
	
	return true;
}