Revit二次开发小技巧（十五）构件的最小矩形外轮廓

news2024/11/26 20:31:08

前言：我们会经常遇到需要计算一个构件的最小外轮廓，一般直接取BoundingBox只有最大和最小值坐标，也是基于x-y坐标系下的。往往不是最小的矩形，所以分享下面的算法来计算最小的外轮廓，条件为法向量是指向Z轴的，暂时没有考虑曲线的情况

背景

需要得到下面构件的最小外接矩形
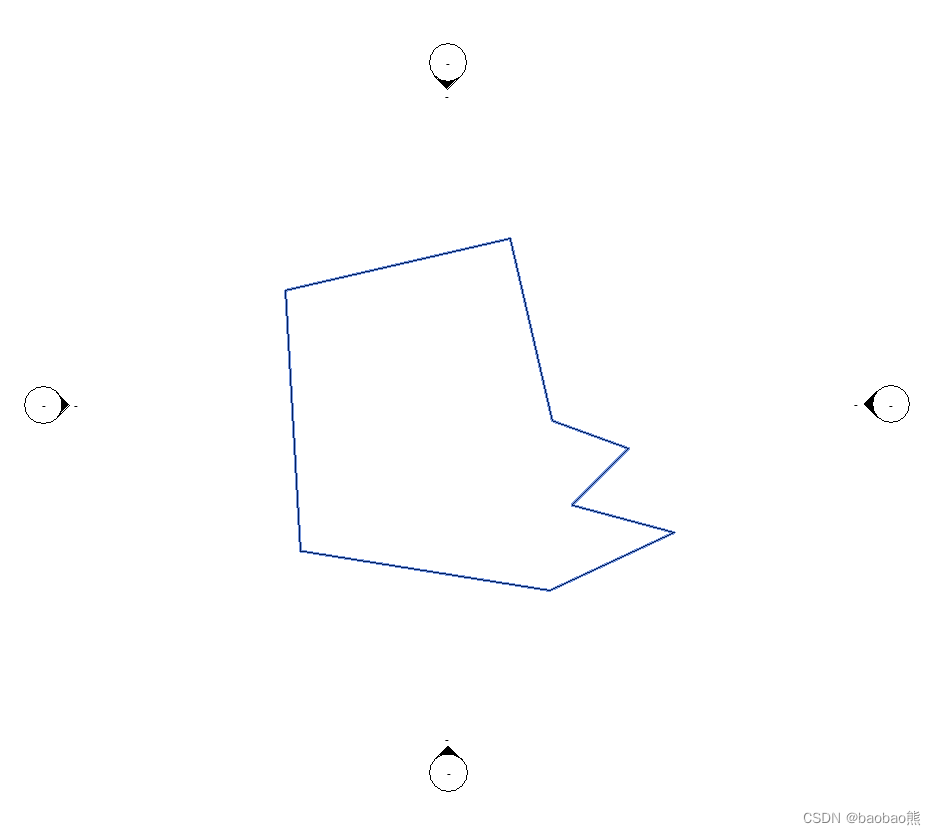
在这里插入图片描述
一般我们使用BoundingBox只能取到最大包络框，而且是基于x-y坐标系下面的。
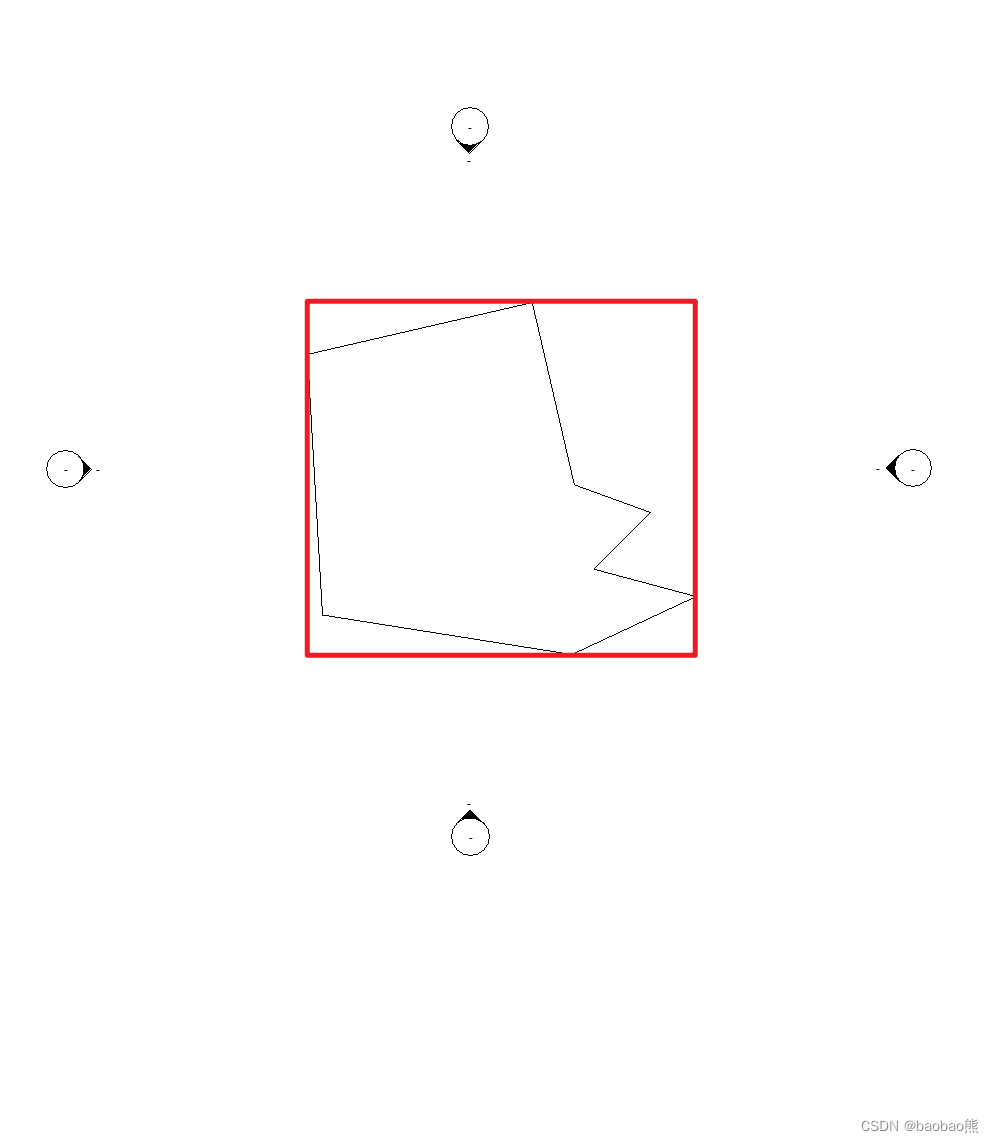
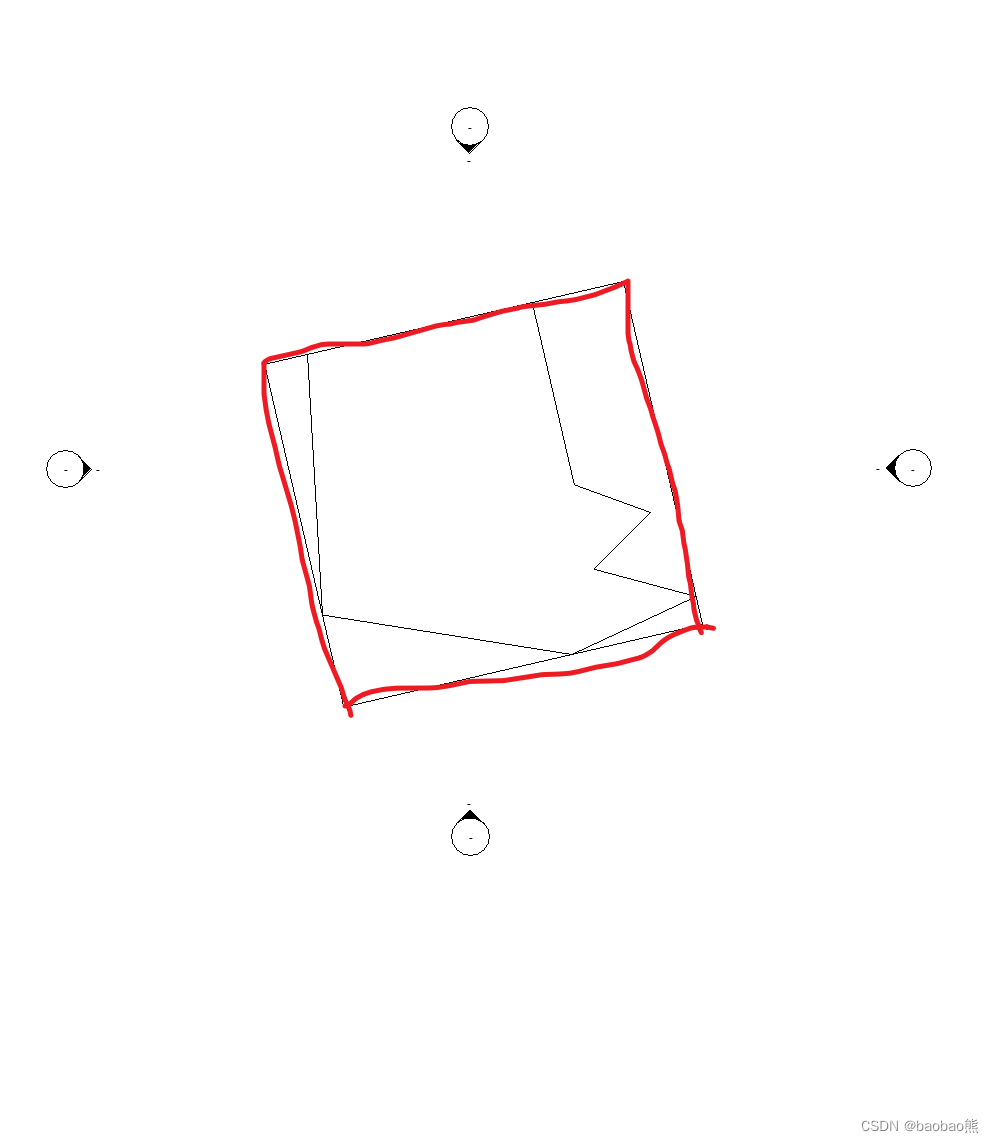
在这里插入图片描述
实际上我们需要的是最小的外接矩形
在这里插入图片描述

代码

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using Autodesk.Revit.UI;
using Autodesk.Revit.DB;
using Autodesk.Revit.Attributes;
using Autodesk.Revit.UI.Selection;

namespace RevitTest
{
    [Transaction(TransactionMode.Manual)]
    public class MinimumBoundingRectangleCmd : IExternalCommand
    {
        public Result Execute(ExternalCommandData commandData, ref string message, ElementSet elements)
        {
            UIDocument uidoc = commandData.Application.ActiveUIDocument;
            Document doc = uidoc.Document;
            Reference selRef;
            try
            {
                selRef = uidoc.Selection.PickObject(ObjectType.Element, "选择构件");
            }
            catch
            {
                return Result.Succeeded;
            }
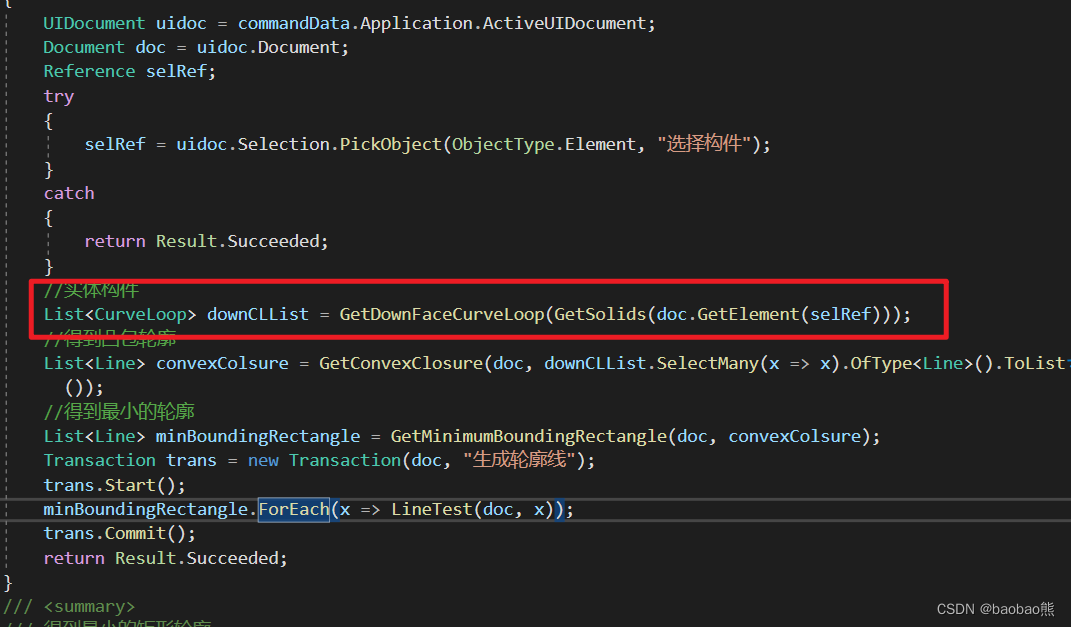
            //实体构件
            List<CurveLoop> downCLList = GetDownFaceCurveLoop(GetSolids(doc.GetElement(selRef)));
            //得到凸包轮廓
            List<Line> convexColsure = GetConvexClosure(doc, downCLList.SelectMany(x => x).OfType<Line>().ToList());
            //得到最小的轮廓
            List<Line> minBoundingRectangle = GetMinimumBoundingRectangle(doc, convexColsure);
            Transaction trans = new Transaction(doc, "生成轮廓线");
            trans.Start();
            minBoundingRectangle.ForEach(x => LineTest(doc, x));
            trans.Commit();
            return Result.Succeeded;
        }
        /// <summary>
        /// 得到最小的矩形轮廓
        /// </summary>
        /// <param name="convexColsure"></param>
        /// <returns></returns>
        public List<Line> GetMinimumBoundingRectangle(Document doc, List<Line> convexColsure)
        {
            List<Line> result = new List<Line>();
            //确定x-y坐标系下最大的外轮廓
            IEnumerable<XYZ> pointList = convexColsure.Select(x => x.GetEndPoint(0));
            double area = double.MaxValue;
            foreach (var l in convexColsure)
            {
                List<Line> rectabgleLineList = GetMinimumBoundingOnPoints(pointList, l.Direction, XYZ.BasisZ.CrossProduct(l.Direction));
                double nwArea = rectabgleLineList[0].Length * rectabgleLineList[1].Length;
                if (nwArea < area)
                {
                    area = nwArea;
                    result = rectabgleLineList;
                }
            }
            return result;
        }
        /// <summary>
        /// 获取点集中的最大点和最小点
        /// </summary>
        /// <param name="points">点集合</param>
        /// <param name="xAxis">x轴</param>
        /// <param name="yAxis">y轴</param>
        /// <returns></returns>
        public List<Line> GetMinimumBoundingOnPoints(IEnumerable<XYZ> points, XYZ xAxis, XYZ yAxis)
        {
            XYZ minPoint = null;
            XYZ maxPoint = null;
            if (points.Count() < 2)
            {
                return null;
            }
            Transform transform = Transform.Identity;
            transform.BasisX = xAxis;
            transform.BasisY = yAxis;
            //取逆矩阵，转回想要的坐标系
            transform = transform.Inverse;
            double minX = int.MaxValue;
            double maxX = int.MinValue;
            double minY = int.MaxValue;
            double maxY = int.MinValue;
            double minZ = int.MaxValue;
            double maxZ = int.MinValue;
            foreach (var xyz in points)
            {
                //转换
                XYZ current = transform == null ? xyz : transform.OfPoint(xyz);
                minX = Math.Min(current.X, minX);
                maxX = Math.Max(current.X, maxX);
                minY = Math.Min(current.Y, minY);
                maxY = Math.Max(current.Y, maxY);
                minZ = Math.Min(current.Z, minZ);
                maxZ = Math.Max(current.Z, maxZ);
            }
            minPoint = new XYZ(minX, minY, minZ);
            maxPoint = new XYZ(maxX, maxY, maxZ);
            XYZ point1 = new XYZ(minX, maxY, maxZ);
            XYZ point2 = new XYZ(maxX, minY, minZ);
            List<Line> result = new List<Line>()
            {
                Line.CreateBound(point1,minPoint).CreateTransformed(transform.Inverse) as Line,
                Line.CreateBound(minPoint,point2).CreateTransformed(transform.Inverse) as Line,
                Line.CreateBound(point2,maxPoint).CreateTransformed(transform.Inverse) as Line,
                Line.CreateBound(maxPoint,point1).CreateTransformed(transform.Inverse) as Line,
            };
            return result;
        }

        /// <summary>
        /// 得到凸包轮廓
        /// </summary>
        /// <param name="doc"></param>
        /// <param name="lines"></param>
        /// <returns></returns>
        public List<Line> GetConvexClosure(Document doc, List<Line> lines)
        {
            List<Line> result = new List<Line>();
            List<XYZ> allPointList = new List<XYZ>();
            lines.ForEach(x =>
            {
                XYZ point1 = SetZ(x.GetEndPoint(0), 0);
                XYZ point2 = SetZ(x.GetEndPoint(1), 0);
                if (allPointList.FirstOrDefault(m => m.DistanceTo(point1) < 1 / 304.8) == null)
                    allPointList.Add(point1);
                if (allPointList.FirstOrDefault(m => m.DistanceTo(point2) < 1 / 304.8) == null)
                    allPointList.Add(point2);
            });
            //找出最x轴最小的点，然后Y轴最小点
            XYZ originPoint = allPointList.OrderBy(x => x.DotProduct(XYZ.BasisX)).ThenBy(x => x.DotProduct(XYZ.BasisY)).FirstOrDefault();
            //LineTest(doc, Line.CreateBound(originPoint, originPoint.Add(XYZ.BasisX * 100)));
            XYZ startPoint = originPoint;
            XYZ endPoint = null;
            while (true)
            {
                if (allPointList.Count == 0) break;
                XYZ startDirection = new XYZ();
                if (endPoint == null)
                    startDirection = -XYZ.BasisY;
                else
                    startDirection = (endPoint - startPoint).Normalize();
                IEnumerable<XYZ> directionList = allPointList.OrderBy(x =>
                {
                    if (x.DistanceTo(startPoint) < 1 / 304.8 || (endPoint != null && x.DistanceTo(endPoint) < 1 / 304.8)) return 1000000000;
                    XYZ direction = (x - startPoint).Normalize();
                    return startDirection.AngleOnPlaneTo(direction, XYZ.BasisZ);
                });
                XYZ onePoint = directionList.FirstOrDefault();
                result.Add(Line.CreateBound(startPoint, onePoint));
                if (onePoint.DistanceTo(originPoint) < 1 / 304.8) break;
                endPoint = startPoint;
                startPoint = onePoint;
            }
            return result;
        }

        /// <summary>
        /// 返回坐标的Z值
        /// </summary>
        /// <param name="point"></param>
        /// <param name="zValue"></param>
        /// <returns></returns>
        public XYZ SetZ(XYZ point, double zValue)
        {
            return new XYZ(point.X, point.Y, zValue);
        }

        /// <summary>
        /// 得到实体集合中的所有底面轮廓集合
        /// </summary>
        /// <param name="solids"></param>
        /// <returns></returns>
        public List<CurveLoop> GetDownFaceCurveLoop(List<Solid> solids)
        {
            List<CurveLoop> result = new List<CurveLoop>();
            List<PlanarFace> topFaceList = new List<PlanarFace>();
            foreach (var s in solids)
            {
                foreach (Face geoFace in s.Faces)
                {
                    PlanarFace temFace = geoFace as PlanarFace;
                    if (temFace == null) continue;
                    if (IsParallel(temFace.FaceNormal, XYZ.BasisZ, false))
                    {
                        topFaceList.Add(temFace);
                        //break;
                    }
                }
            }

            foreach (var topFace in topFaceList)
            {
                var curveLoopList = topFace.GetEdgesAsCurveLoops().ToList();
                result.AddRange(curveLoopList);
            }
            return result;
        }
        /// <summary>
        /// 计算两点平面上的距离
        /// </summary>
        /// <param name="onePoint"></param>
        /// <param name="twoPoint"></param>
        /// <returns></returns>
        public double GetHorizontalDistance(XYZ onePoint, XYZ twoPoint)
        {
            return Math.Pow(Math.Pow(onePoint.X - twoPoint.X, 2) + Math.Pow(onePoint.Y - twoPoint.Y, 2), 0.5);
        }

        /// <summary>
        /// 生成直线
        /// </summary>
        /// <param name="doc"></param>
        /// <param name="l"></param>
        /// <returns></returns>
        public ModelCurve LineTest(Document doc, Line l)
        {
            XYZ basicZ = XYZ.BasisZ;
            if (l.Direction.AngleTo(XYZ.BasisZ) < 0.0001 || l.Direction.AngleTo(-XYZ.BasisZ) < 0.0001)
                basicZ = XYZ.BasisY;
            XYZ normal = basicZ.CrossProduct(l.Direction).Normalize();

            Plane plane = Plane.CreateByNormalAndOrigin(normal, l.GetEndPoint(0));

            Transaction transCreate = null;
            if (!doc.IsModifiable)
                transCreate = new Transaction(doc, "模型线测试");
            transCreate?.Start();
            SketchPlane sktpl = SketchPlane.Create(doc, plane);
            ModelCurve mc = doc.IsFamilyDocument ? doc.FamilyCreate.NewModelCurve(l, sktpl) : doc.Create.NewModelCurve(l, sktpl);
            transCreate?.Commit();
            return mc;
        }
        /// <summary>
        /// 拿到对应构件的Solid集合
        /// </summary>
        /// <param name="elem"></param>
        /// <param name="vdtLevel"></param>
        /// <returns></returns>
        public List<Solid> GetSolids(Element elem, ViewDetailLevel vdtLevel = ViewDetailLevel.Fine)
        {
            if (elem == null)
            {
                return new List<Solid>();
            }
            GeometryElement geometryElement = elem.get_Geometry(new Options
            {
                ComputeReferences = true,
                DetailLevel = vdtLevel,
                IncludeNonVisibleObjects = false,
            });
            return GetSolids(geometryElement);
        }
        /// <summary>
        /// 获取所有的Solid
        /// </summary>
        /// <param name="geometryElement"></param>
        /// <returns></returns>
        public List<Solid> GetSolids(GeometryElement geometryElement)
        {
            List<Solid> result = new List<Solid>();
            foreach (GeometryObject geomObj in geometryElement)
            {
                Solid solid = geomObj as Solid;
                if (null != solid)
                {
                    result.Add(solid);
                    continue;
                }
                //If this GeometryObject is Instance, call AddCurvesAndSolids
                GeometryInstance geomInst = geomObj as GeometryInstance;
                if (null != geomInst)
                {
                    GeometryElement transformedGeomElem = geomInst.GetInstanceGeometry(Transform.Identity);
                    result.AddRange(GetSolids(transformedGeomElem));
                }
            }
            return result;
        }
        /// <summary>
        /// 得到实体指定方向的一开始的面(取该方向上最里面的面)
        /// </summary>
        /// <param name="targetSolid"></param>
        /// <returns></returns>
        public List<CurveLoop> GetDirectionOriginCurveLoop(Solid targetSolid, XYZ direction)
        {
            List<CurveLoop> result = new List<CurveLoop>();
            List<PlanarFace> topFaceList = new List<PlanarFace>();
            foreach (Face geoFace in targetSolid.Faces)
            {
                PlanarFace temFace = geoFace as PlanarFace;
                if (temFace == null) continue;
                if (IsParallel(temFace.FaceNormal, direction))
                {
                    topFaceList.Add(temFace);
                }
            }
            var topFace = topFaceList.OrderBy(x => x.Origin.DotProduct(direction)).FirstOrDefault();
            var curveLoopList = topFace.GetEdgesAsCurveLoops().ToList();
            result.AddRange(curveLoopList);
            return result;
        }
        /// <summary>
        /// 向量是否平行
        /// </summary>
        /// <param name="vector1"></param>
        /// <param name="vector2"></param>
        /// <param name="v">true为同向平行，false为反向平行，null为平行</param>
        /// <param name="tolerance">允许误差的角度</param>
        /// <returns></returns>
        public bool IsParallel(XYZ vector1, XYZ vector2, bool? v = null, double tolerance = 0.1)
        {
            var angle = vector1.AngleTo(vector2) / Math.PI * 180;
            if (v == null)
            {
                return angle >= 180 - tolerance || angle <= tolerance;
            }
            else if (v == true)
            {
                return angle <= tolerance;
            }
            else
            {
                return angle >= 180 - tolerance;
            }
        }
        /// <summary>
        /// 传入集合的集合体，批量操作
        /// </summary>
        /// <param name="solids"></param>
        /// <param name="booleanOperationsType"></param>
        /// <returns></returns>
        public Solid GetUnionSolid(List<Solid> solids, BooleanOperationsType booleanOperationsType)
        {
            Solid firstSolid = solids[0];
            solids.RemoveAt(0);
            //对所有的几何体进行融合
            foreach (var oneSoild in solids)
            {
                try
                {
                    firstSolid = SolidBooleanOperation(firstSolid, oneSoild, booleanOperationsType);
                }
                catch
                {

                }

            }
            return firstSolid;
        }
        /// <summary>
        /// Solid布尔操作
        /// </summary>
        /// <param name="solidA"></param>
        /// <param name="solidB"></param>
        /// <param name="booleanOperationsType"></param>
        /// <returns></returns>
        public Solid SolidBooleanOperation(Solid solidA, Solid solidB, BooleanOperationsType booleanOperationsType)
        {
            Solid result = null;
            try
            {
                result = BooleanOperationsUtils.ExecuteBooleanOperation(solidA, solidB, booleanOperationsType);
            }
            catch (Exception ex)
            {
                result = BooleanOperationsUtils.ExecuteBooleanOperation(solidB, solidA, booleanOperationsType);
            }
            return result;
        }

    }
}

思路

一、确定底面轮廓线

通过找到构件的所有底面，然后返回所有的面的轮廓线
在这里插入图片描述

二、根据轮廓线计算凸包轮廓

把线的起终点都添加到集合里面，然后去重。由于我们当前方法仅处理法向量为XYZ.BasisZ的平面，需要把所有的点都降到统一的平面上，默认Z轴为0。
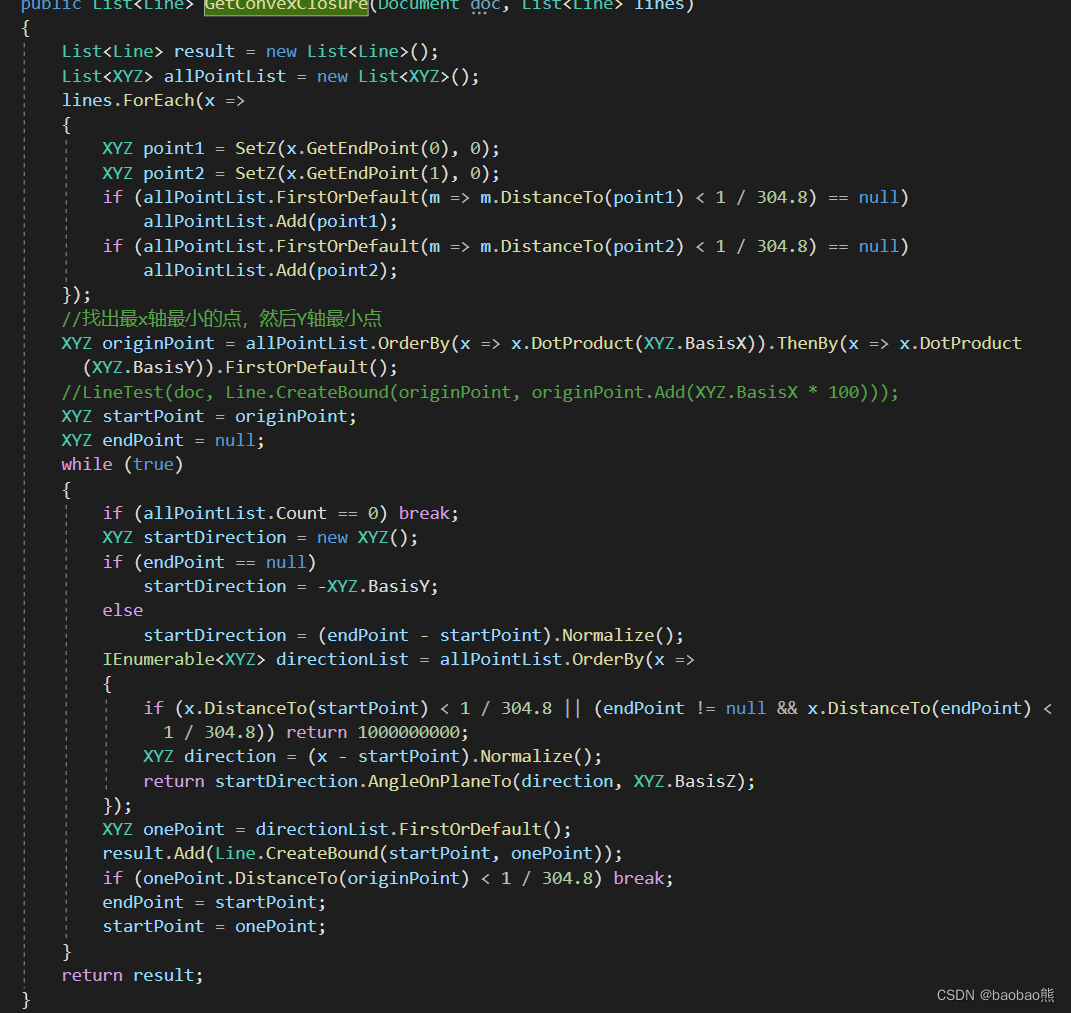
在这里插入图片描述
凸包算法的思路：

  1. 找到X轴和Y轴数值最小的点，确定为原点，也为起点
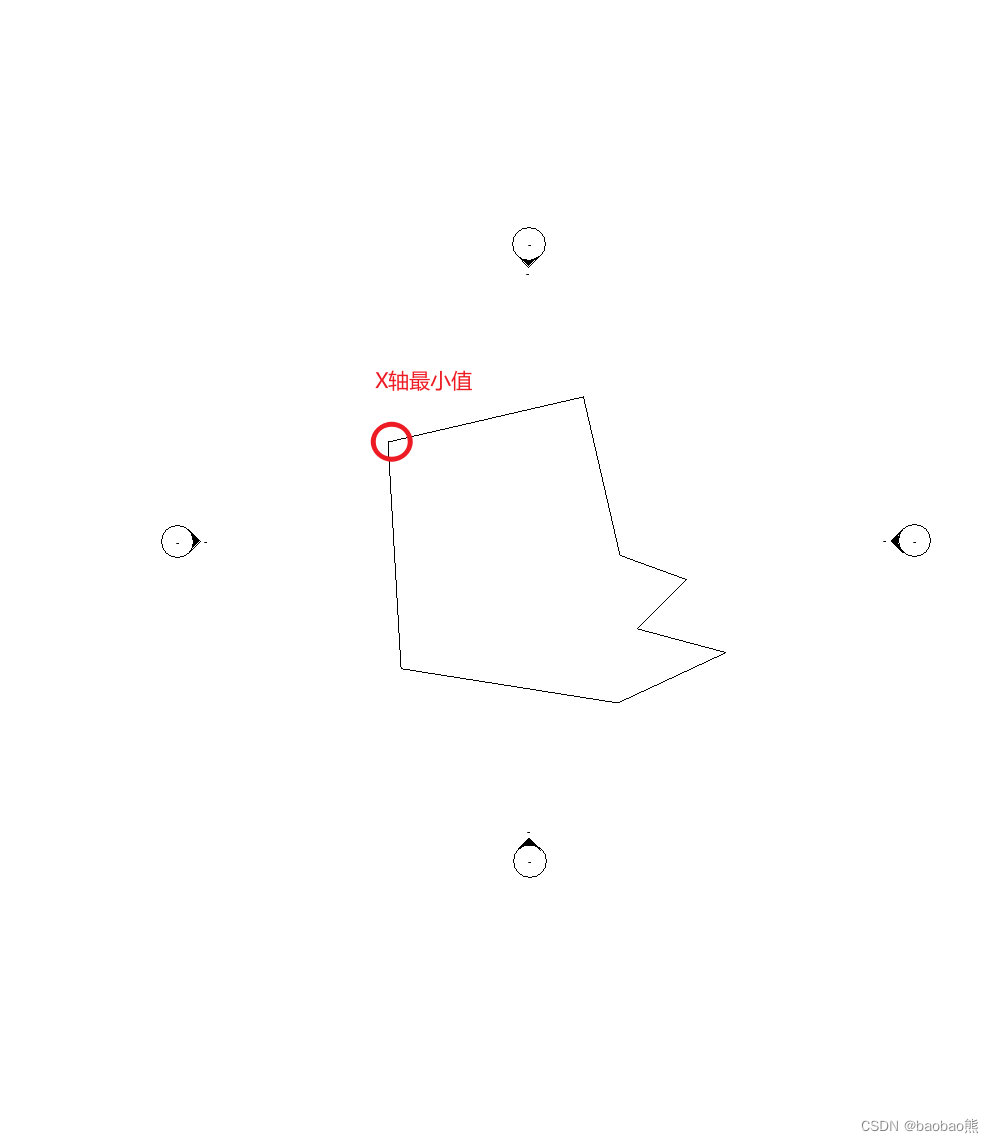
    在这里插入图片描述

  2. 默认开始的方向为-Y轴的方向
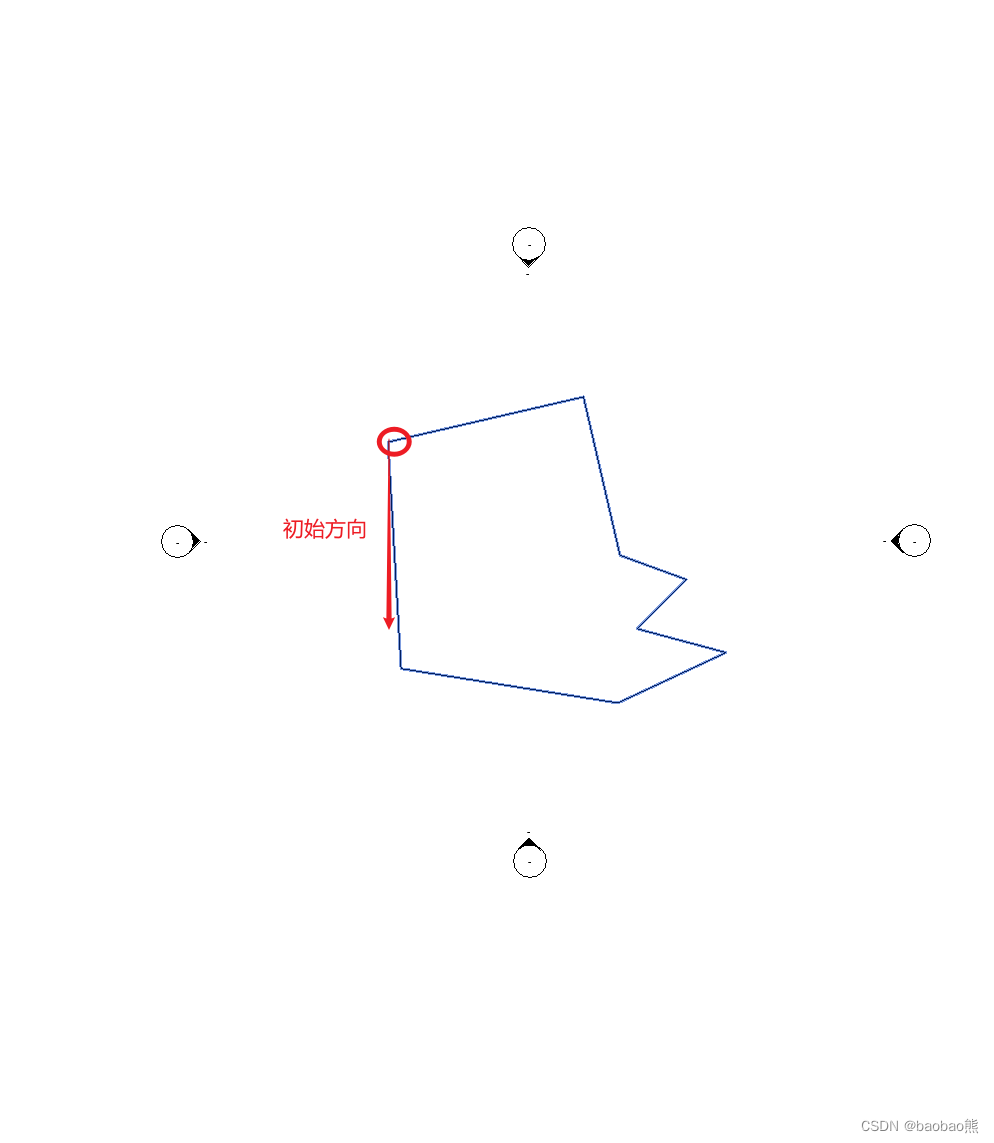
    在这里插入图片描述

  3. 根据点集里面的点，分别构建一个起点出发，指向其他点的向量。
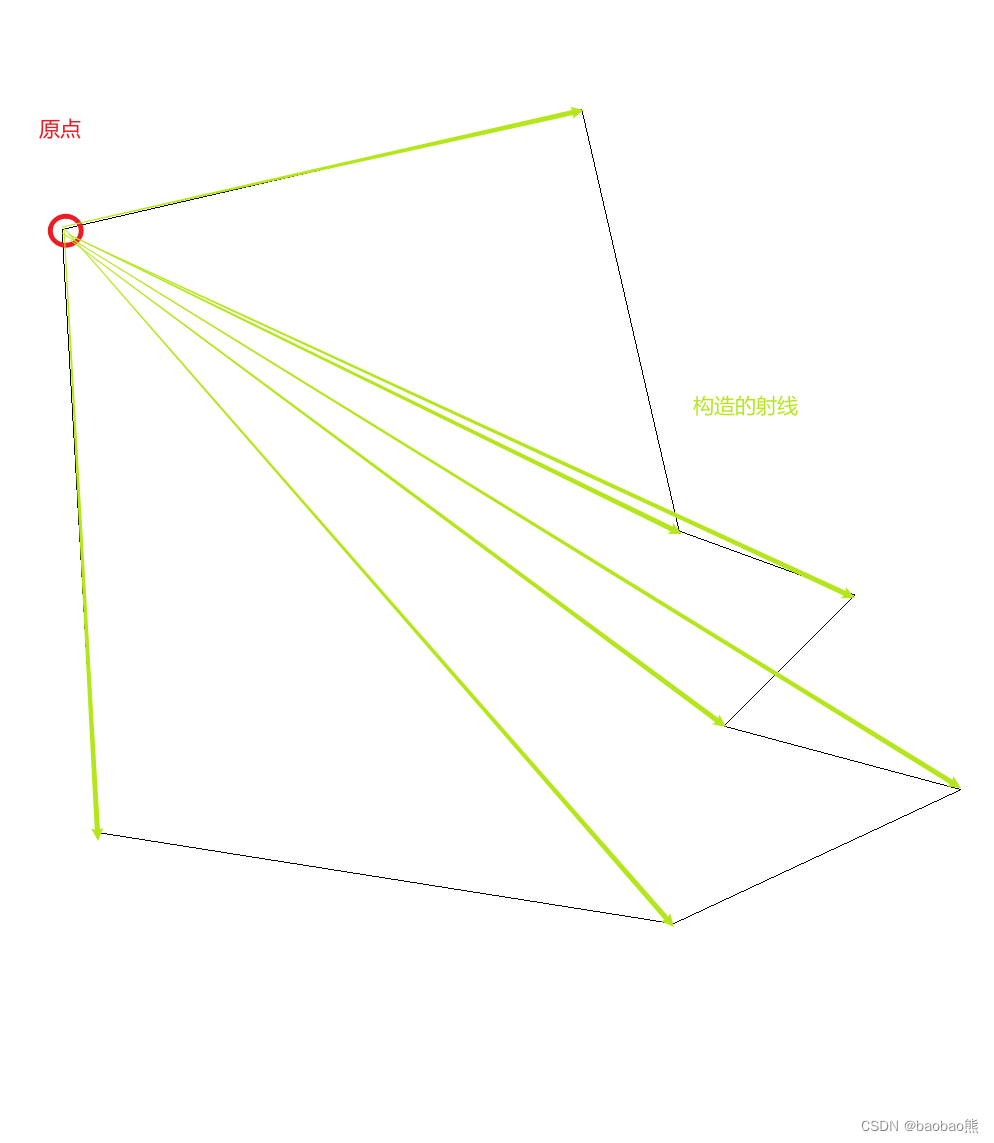
    在这里插入图片描述

  4. 如果是原点的时候，就找-Y轴和哪个点构造的向量的逆时针夹角最小。这个点就是我们要的下一个凸点。
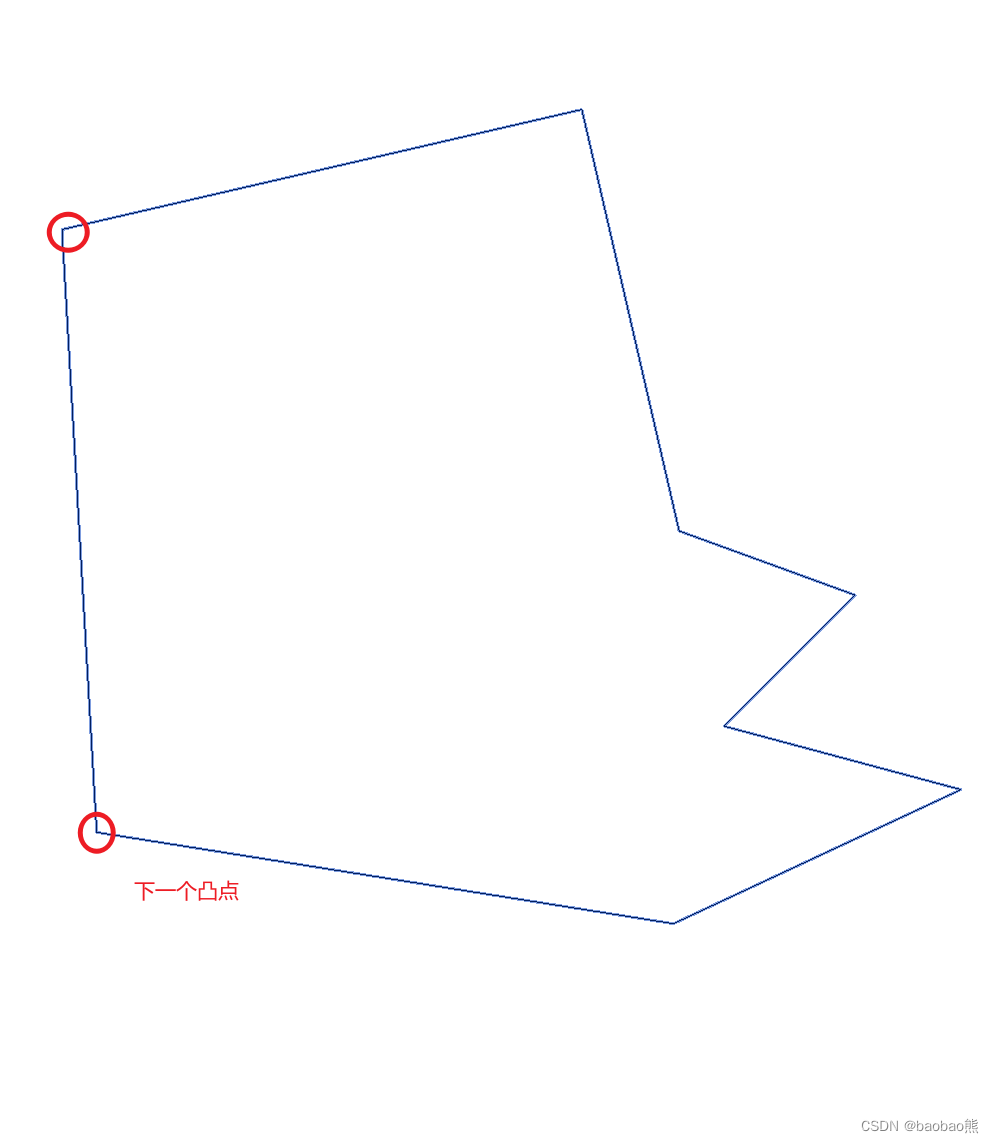
    在这里插入图片描述

  5. 以找到的凸点为起点，找到的凸点和上一个凸点的向量为初始向量。重复构造点集向量，找最小夹角的过程。

  6. 在回到原点的时候，寻找结束。
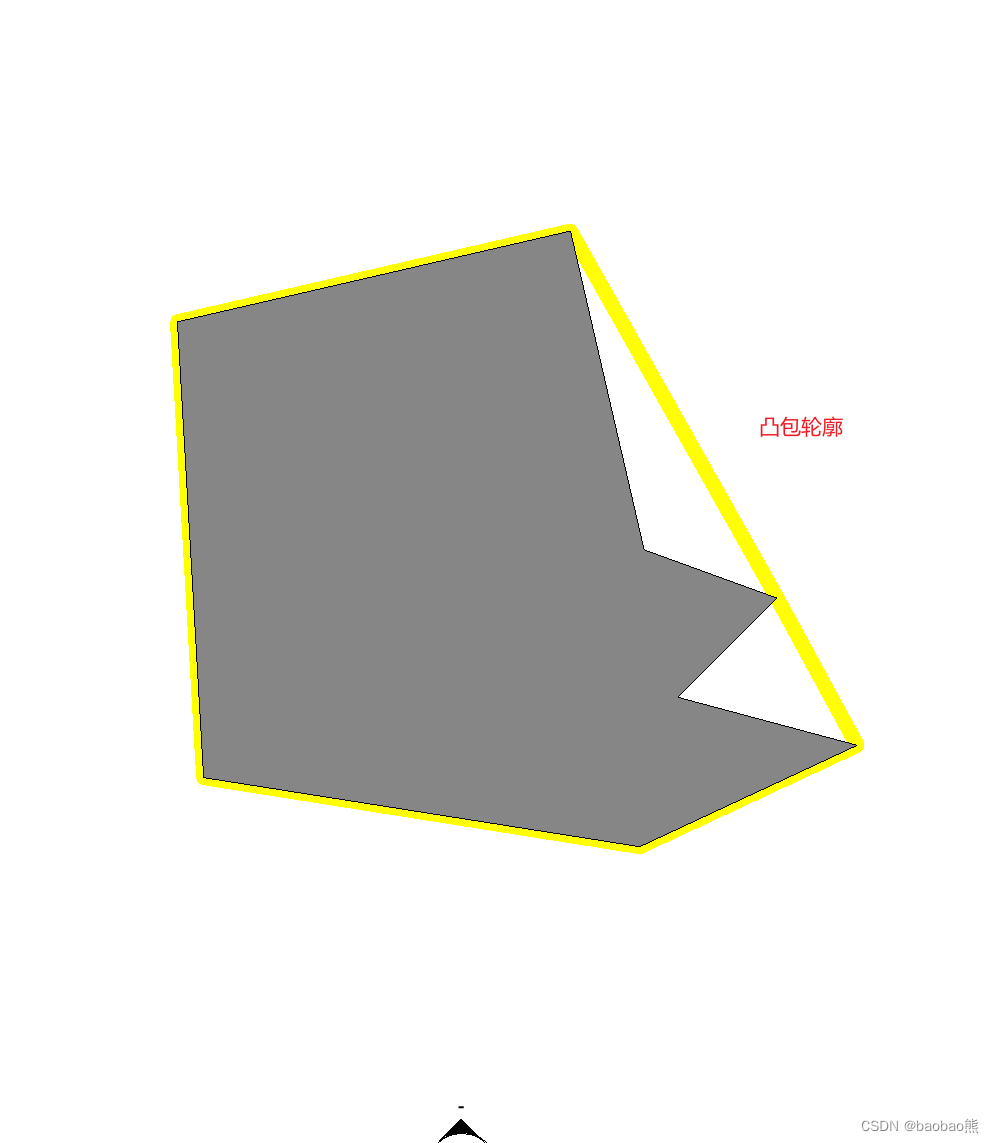
    在这里插入图片描述

三、根据凸包轮廓生成矩形轮廓

  1. 以凸包轮廓的每一条线的方向为X轴，通过Z轴和X轴的叉乘得到Y轴
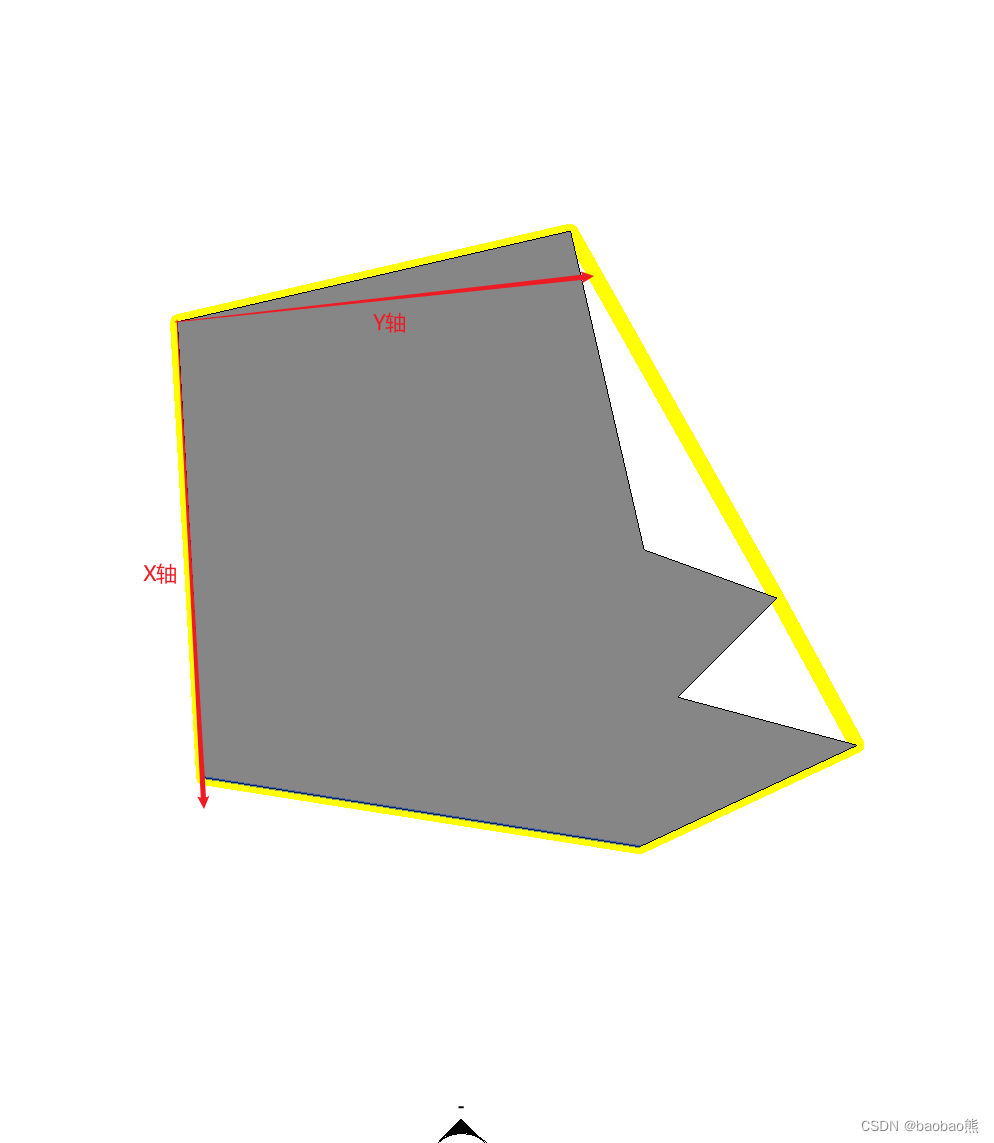
    在这里插入图片描述

  2. 以X和Y轴的单位向量，构建一个Transform对象，并把BasisX和BasisY设置组成对应的XY轴方向。（相当于把构件以点旋转了一定角度，把坐标系变成我们要的坐标系）
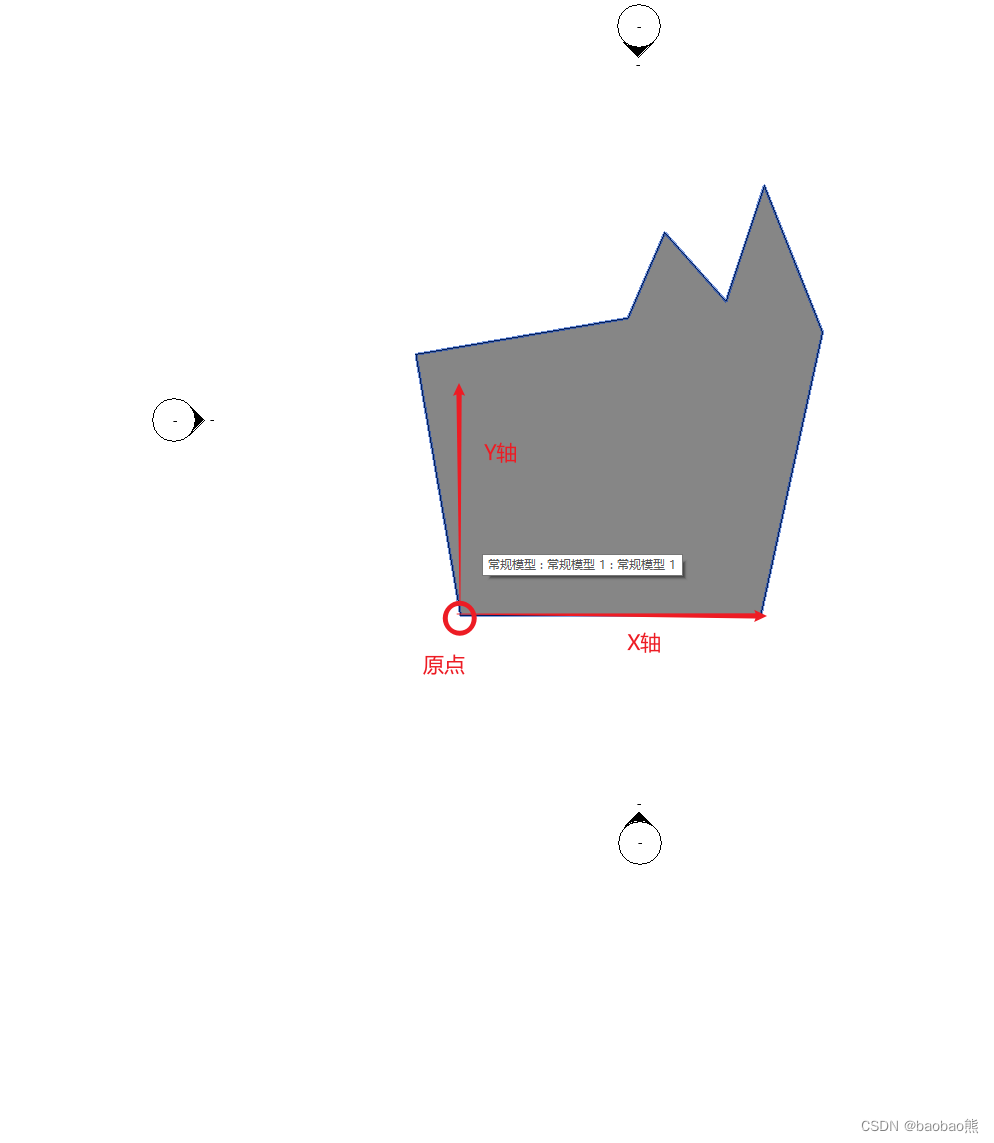
    在这里插入图片描述

  3. 把所有的点都转到以我们需要的XY轴的坐标系下，再计算四个角点，并连成矩形。得到的线再转回到项目的坐标下，就得到这条边对应的外接矩形了。
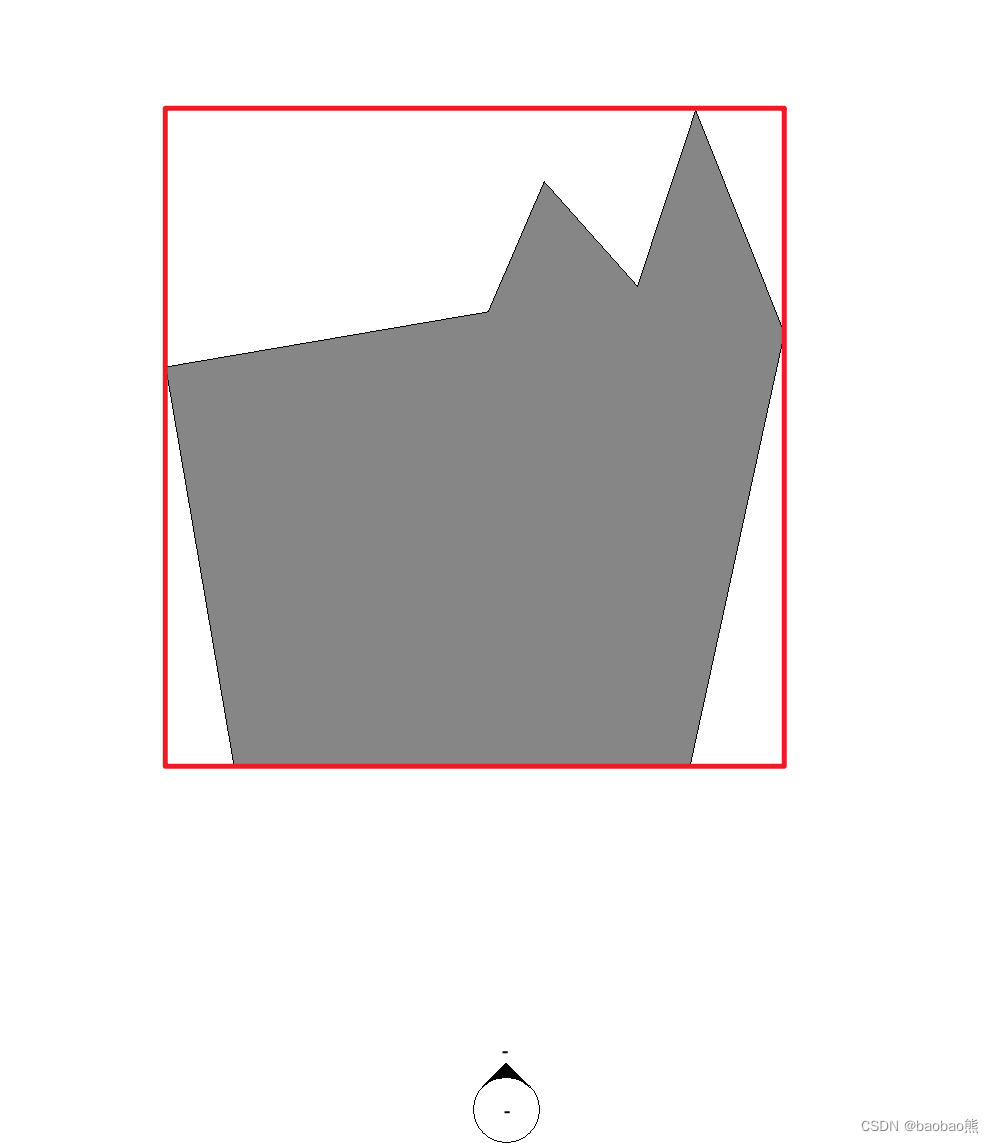
    在这里插入图片描述

  4. 所有的边都计算一个外接矩形，然后得到哪个外接矩形面积最小，就是我们要的那个了。
    在这里插入图片描述

写在最后

希望这篇文章可以给你带来帮助~~~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/92377.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

mqtt服务器搭建与qt下的mqtt客户端实现

mqtt服务器搭建与qt下的mqtt客户端实现

一、mqtt介绍 MQTT&#xff08;Message Queuing Telemetry Transport&#xff0c;消息队列遥测传输协议&#xff09;&#xff0c;是一个基于客户端-服务器的消息发布/订阅传输协议。MQTT协议是轻量、简单、开放和易于实现的&#xff0c;这些特点使它适用范围非常广泛。在很多情…
阅读更多...
前端基础(九)_CSS的三大特征

前端基础(九)_CSS的三大特征

CSS的三大特征 1、层叠性 1.样式冲突&#xff0c;遵循就近原则 2.样式不冲突&#xff0c;不会层叠&#xff0c;会叠加 1.1.样式冲突&#xff0c;遵循就近原则例子&#xff1a; <!DOCTYPE html> <html lang"en"><head><meta charset"UT…
阅读更多...
[附源码]Nodejs计算机毕业设计基于的服装商城系统Express(程序+LW)

[附源码]Nodejs计算机毕业设计基于的服装商城系统Express(程序+LW)

该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程。欢迎交流 项目运行 环境配置&#xff1a; Node.js Vscode Mysql5.7 HBuilderXNavicat11VueExpress。 项目技术&#xff1a; Express框架 Node.js Vue 等等组成&#xff0c;B/S模式 Vscode管理前后端分…
阅读更多...
Java优雅的记录日志：log4j实战篇

Java优雅的记录日志：log4j实战篇

写在前面 项目开发中&#xff0c;记录错误日志有以下好处&#xff1a; 方便调试 便于发现系统运行过程中的错误 存储业务数据&#xff0c;便于后期分析 在java中&#xff0c;记录日志有很多种方式&#xff1a; 自己实现&#xff1a;自己写类&#xff0c;将日志数据&#xf…
阅读更多...
HTTP Range：范围请求

HTTP Range：范围请求

文章目录HTTP 范围请求HTTP 范围请求 Range 头是在 HTTP/1.1 协议中新增的一个请求头。包含 Range 头的请求通常称为范围请求&#xff0c;因为 Range 头允许服务器只发送部分响应到客户端&#xff0c;它是下载工具&#xff08;例如迅雷&#xff09;实现多线程下载的核心所在&a…
阅读更多...
Python -- 列表

Python -- 列表

目录 1.列表的基本使用 1.1 列表的格式 1.2 使用下标获取列表元素 2.列表的增删改查 2.1 添加元素 2.2 修改元素 2.3 查找元素 2.4 删除元素 2.5 排序&#xff08;sort、reverse&#xff09; 3.列表遍历 3.1 使用while循环 3.2 使用for循环 4.列表的嵌套 1.列表的基本…
阅读更多...
面向切面编程 AOP

面向切面编程 AOP

AOPAOP的概念AOP &#xff08;底层原理&#xff09;AOP 底层使用动态代理AOP &#xff08; JDK 动态代理&#xff09;首先我们来看一下 Spring 的百度百科   Spring 框架是一个开放源代码的 J2EE 应用程序框架&#xff0c;由 Rod Johnson 发起&#xff0c;是针对 Bean 的生命…
阅读更多...
cpp项目中遇到的一些错误

cpp项目中遇到的一些错误

1.解决由于找不到xxx.dll&#xff0c;无法继续执行代码的问题 解决由于找不到xxx.dll&#xff0c;无法继续执行代码的问题_happylife_mini的博客-CSDN博客_由于找不到emp.dll无法继续执行代码在用vs写项目&#xff0c;或者你下载github上的C代码的时候&#xff0c;是不是经常遇…
阅读更多...
【Redis技术探索】「底层架构原理」探索分析服务系统的网络架构和线程模型

【Redis技术探索】「底层架构原理」探索分析服务系统的网络架构和线程模型

Redis网络基础架构 网络编程离不开Socket&#xff0c;网络I/O模型最常用的无非是同步阻塞、同步非阻塞、异步阻塞、异步非阻塞&#xff0c;高性能网络服务器最常见的线程模型也就是基于EventLoop模式的单线程模型。 Redis基础组建结构 Redis网络层基础组件主要包括四个部分&a…
阅读更多...
acm是什么？你准备好去打了吗？（未完结）

acm是什么？你准备好去打了吗？（未完结）

1.引言2.acm究竟是什么&#xff1f;3.acm的时间安排4.acm该如何准备1.引言 作为一个零基础的小白&#xff0c;acm这条路走的并不顺畅&#xff0c;接触的信息很少&#xff0c;以至于在这条道路上走了不少弯路&#xff0c;浪费了大量的时间&#xff0c;现在也快要退役的阶段&…
阅读更多...
Linux基础-软件包管理器RPM与yum

Linux基础-软件包管理器RPM与yum

该文章主要为完成实训任务&#xff0c;详细实现过程及结果见【参考文章】 参考文章&#xff1a;https://howard2005.blog.csdn.net/article/details/127131286?spm1001.2014.3001.5502 文章目录一、使用RPM软件包管理器1. RPM安装软件包2. RPM更新与升级软件包3. RPM查询软件包…
阅读更多...
Qt-Web混合开发-Qt读写Json数据（5）

Qt-Web混合开发-Qt读写Json数据（5）

Qt-Web混合开发-Qt使用内置json库读写json示例&#x1f34f; 文章目录Qt-Web混合开发-Qt使用内置json库读写json示例&#x1f34f;1、概述&#x1f353;2、实现效果&#x1f345;3、实现功能&#x1f95d;4、关键代码&#x1f33d;5、源代码&#x1f346;更多精彩内容&#x1f…
阅读更多...
面试怎么回答MySQL索引问题，看这里

面试怎么回答MySQL索引问题，看这里

前言 小A在宿舍里跟哥们开五黑打排位中&#xff0c;突然收到女神小美的消息&#xff1a;“小A&#xff0c;我今天面试碰到索引问题了&#xff0c;我没回答好”。小A顾不上游戏抓紧回复到&#xff1a;“到你宿舍某某咖啡店吧&#xff0c;我帮你一起看下”。 小A抓紧时间换了衣…
阅读更多...
物联公司网页设计制作 简单静态HTML网页作品 静态企业网页作业成品 学生网站模板

物联公司网页设计制作 简单静态HTML网页作品 静态企业网页作业成品 学生网站模板

&#x1f389;精彩专栏推荐 &#x1f4ad;文末获取联系 ✍️ 作者简介: 一个热爱把逻辑思维转变为代码的技术博主 &#x1f482; 作者主页: 【主页——&#x1f680;获取更多优质源码】 &#x1f393; web前端期末大作业&#xff1a; 【&#x1f4da;毕设项目精品实战案例 (10…
阅读更多...
Linux系统部署

Linux系统部署

Linux系统部署 下载vmware centos7 xshell6 xftp6新建虚拟机&#xff0c;注意设置网络连接&#xff0c;设置登录名&#xff1a;root,密码&#xff1a;root,等待登录&#xff0c;输入用户名和密码&#xff08;注意密码输入不显示&#xff09;登录成功&#xff0c;执行命令Ifc…
阅读更多...
【网管日记】MySQL主从复制

【网管日记】MySQL主从复制

MySQL主从复制 基本介绍 MySQL 主从复制是一个异步的复制过程&#xff0c;底层是基于 Mysql 数据库自带的 二进制日志 功能。 一台或多台 MySQL 数据库&#xff08;slave&#xff0c;即 从库 &#xff09;从另一台 MySQL 数据库&#xff08; master&#xff0c;即 主库 &…
阅读更多...
餐饮后台管理系统

餐饮后台管理系统

一、项目介绍&#xff1a; 用于每天的菜品数据分析&#xff0c;客户的管理&#xff0c;员工的管理&#xff0c;查看订单信息&#xff0c;菜品的添加或者下架管理 二、项目使用技术栈&#xff1a; vue2全家桶、element-ui、axios、js、es6、echarts 三、主页效果图&#xff…
阅读更多...
pytorch深度学习实战一书，tensorboard可视化踩坑

pytorch深度学习实战一书，tensorboard可视化踩坑

书评&踩坑[TOC](书评&踩坑) 提示&#xff1a;纯个人观点&#xff0c;仅供参考前言一、源码学习&#xff0c;又是版本问题&#xff08;省略内心独白...&#xff09;二、步骤1.安装tensorflow2.思考&#xff0c;看代码&#xff0c;看书求证总结提示&#xff1a;纯个人观点…
阅读更多...
卧兔CEO胡煜受邀参加2022世界直播电商大会

卧兔CEO胡煜受邀参加2022世界直播电商大会

首届全球数字贸易博览会于12月11日在国际博览中心盛大开幕。在这个国家级、全球性、专业性的舞台上&#xff0c;“2022世界直播电商大会”作为分论坛&#xff0c;精彩启幕。 “2022世界直播电商大会”由浙江省人民政府和商务部联合主办&#xff0c;杭州市人民政府和浙江省商务…
阅读更多...
借款久期还款久期 简述

借款久期还款久期 简述

借款久期&还款久期 简述 在工作的时候&#xff0c;在资产使用遇到三个指标&#xff0c;分别是生息资产、借款久期、还款久期&#xff0c;有点不清楚其中的含义&#xff0c;查阅相关资料后做个简短的总结&#xff0c;可能有错&#xff0c;先放这。 1 久期 久期&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023