二叉搜索树的特性

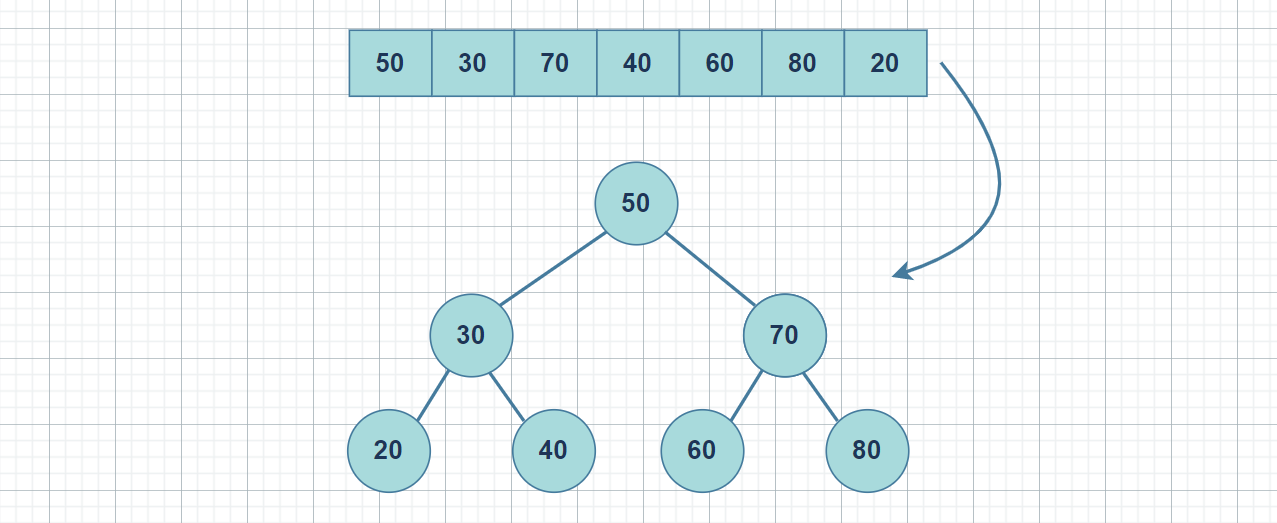
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

二叉搜索树的主要用途

二叉搜索树主要用于实现高效的数据查找和排序：

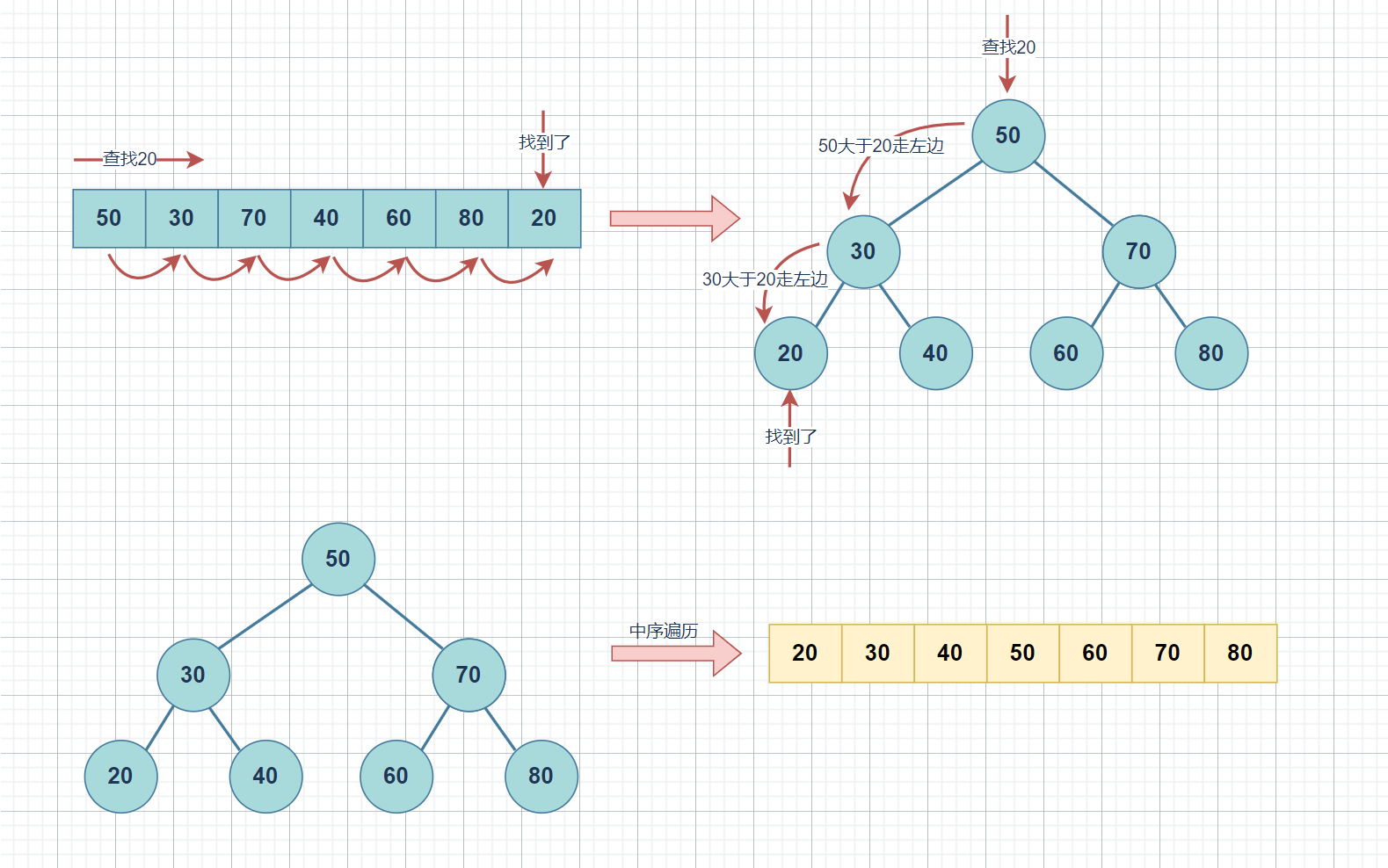
查找：由于二叉搜索树的特性，可以通过比较节点的键值来快速定位目标节点。在查找操作中，对于一颗相对平衡的二叉搜索树，每次都可以将搜索范围缩小一半，因此平均时间复杂度为O(log n)，其中n是树中节点的数量。
排序：对于一个无序的序列，可以利用二叉搜索树的性质进行排序。具体实现方法是，将序列中的元素依次插入到二叉搜索树中，然后进行中序遍历，即可按照升序输出有序序列。这种基于二叉搜索树的排序算法，对于一颗相对平衡的二叉搜索树，平均时间复杂度为O(nlog n)

在这里插入图片描述

需要注意的是，二叉搜索树的性能取决于树的形状。如果构建出的二叉搜索树高度不平衡（只有左树或只有右树），查找的时间复杂度可能达到O(n)，导致操作效率会大幅下降。因此，在实际使用中，需要注意维护二叉搜索树的平衡性，以提高操作效率，在此基础上演化出了 AVL树、红黑树等更具平衡性的数据结构。

二叉搜索树是学习其他“搜索”数据结构的基础，下面就围绕二叉搜索树的一些操作进行展开介绍：

二叉搜索树的基本操作

为了实现二叉搜索树的相关操作，这里首先给出二叉搜索树节点的定义：

static class TreeNode {
 	 public int val;
     public TreeNode left;
     public TreeNode right;

     public TreeNode(int val) {
         this.val = val;
     }
 }
// 二叉搜索树根节点，初始时为空
public TreeNode root = null;

1、二叉搜索树的查找

实现思路（利用二叉搜索树的特性）：

从根节点开始，与目标键值进行比较。
如果目标键值等于当前节点的键值，则找到了目标节点；
如果目标键值小于当前节点的键值，则继续在左子树中查找；
如果目标键值大于当前节点的键值，则继续在右子树中查找；
重复步骤2、3、4直到找到目标节点或者遍历到叶子节点。

public TreeNode find(int val) {
    // 从根节点开始查找
    TreeNode cur = root;
    while (cur != null) {
        if (cur.val == val) {
            // 找到返回结点
            return cur;
        } else if (cur.val > val) {
            // 当前结点值大于目标结点
            cur = cur.left;
        } else {
            // 当前结点小于目标结点
            cur = cur.right;
        }
    }
    // 找不到
    return null;
}

2、二叉搜索树的插入

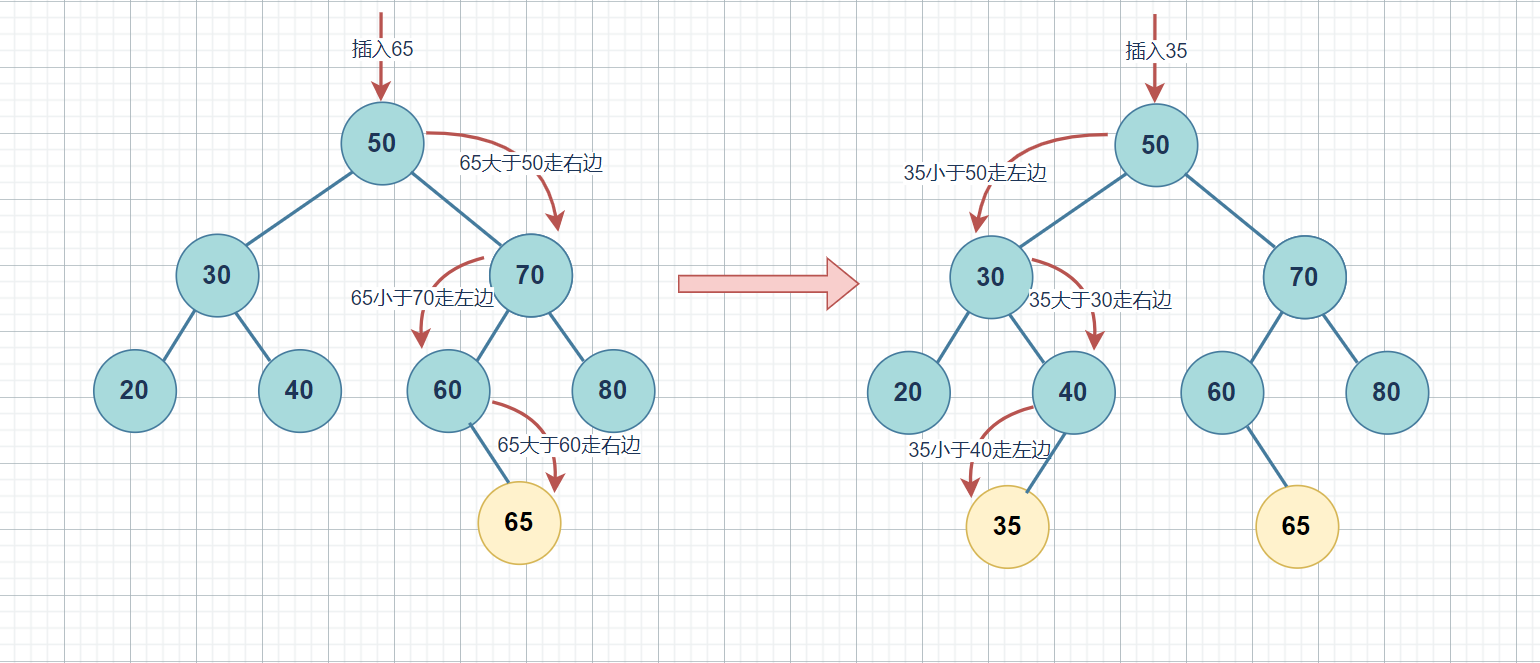
经过简单分析，当搜索树非空时，二叉树的插入，总是插入到相应的叶子结点（由于结点之间单向联通，所以需要记录待插入位置的父节点）：

从根节点开始，与要插入的键值进行比较。
如果要插入的键值小于当前节点的键值并且当前节点的左子节点为空，则将新节点作为当前节点的左子节点；
如果要插入的键值大于当前节点的键值并且当前节点的右子节点为空，则将新节点作为当前节点的右子节点。

public boolean insert(int val) {
    // 如果当前根节点为空，则插入到根节点
    if (root == null) {
        root = new TreeNode(val);
        return true;
    }
    TreeNode cur = root;
    // 记录插入位置的父节点
    TreeNode parent = null;
    // 寻找插入位置
    while (cur != null) {
        if (cur.val > val) {
        	// 当前结点值大于目标结点
            parent = cur;
            cur = cur.left;
        } else if (cur.val < val) {
        	// 当前结点值小于目标结点
            parent = cur;
            cur = cur.right;
        } else {
            // 如果二叉搜索树中已存在，直接返回
            System.out.println("已存在:" + val);
            return false;
        }
    }
    // 构造插入结点
    TreeNode node = new TreeNode(val);
    // 此时 parent 结点指向插入位置的父节点
    if (parent.val > val) {
        parent.left = node;
    } else {
        parent.right = node;
    }
    return true;
}

3、二叉搜索树的删除（难点）

（1）找到待删结点

二叉搜索树的删除，首先需要找到待删除结点，然后执行删除操作（由于结点之间单向联通，所以需要记录待删结点的父节点）：

public void remove(int val) {
	// 待删结点，从root开始找
    TreeNode cur = root;
    // 待删结点的父节点
    TreeNode parent = null;
    while (cur != null) {
        if (cur.val == val) {
        	// 找到目标结点，调用删除操作
            removeNode(cur, parent);
            return;
        } else if (cur.val > val) {
        	// 当前结点值大于目标结点
            parent = cur;
            cur = cur.left;
        } else {
        	// 当前结点值小于目标结点
            parent = cur;
            cur = cur.right;
        }
    }
    System.out.println("不存在：" + val);
}

（2）分情况删除

二叉搜索树的删除操作，是一个相对复杂的操作，需要考虑多种不同情况：

设待删除结点为 cur, 待删除结点的双亲结点为 parent

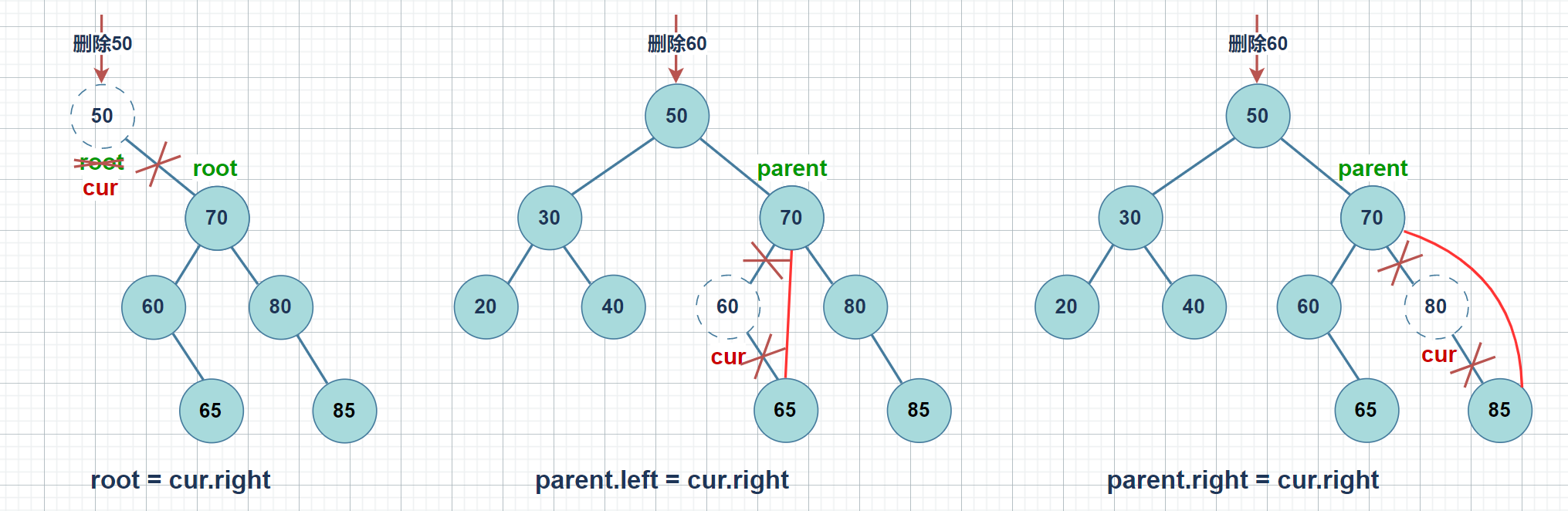
cur.left == null

思路：

cur 是 root，则 root = cur.right
cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
cur 不是 root，cur 是 parent.right，则 parent.right = cur.right

cur.right == null

思路：

cur 是 root，则 root = cur.left
cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
cur 不是 root，cur 是 parent.right，则 parent.right = cur.left

cur.left != null && cur.right != null

思路：

此时需要使用替换法进行删除。可以选择用其左子树cur.left的最大值节点，或右子树cur.right的最小值节点的值填补到被删除节点中，然后删除这个最大或最小值节点。

上面这两种选哪个都行，下面我就以选择右子树 cur.right 中的最小值结点替换删除为例：

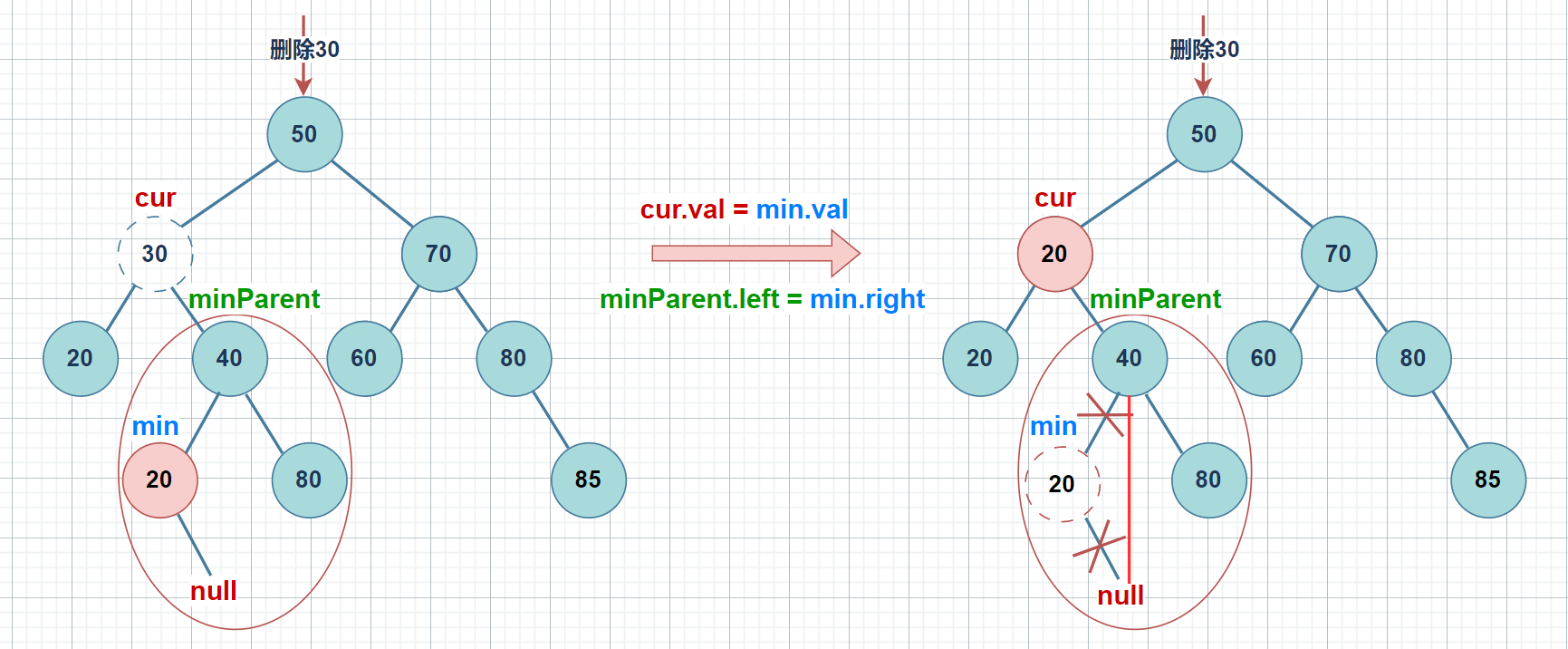
当右子树的根节点有左孩子，那么 minParent.left 是右子树的最小值

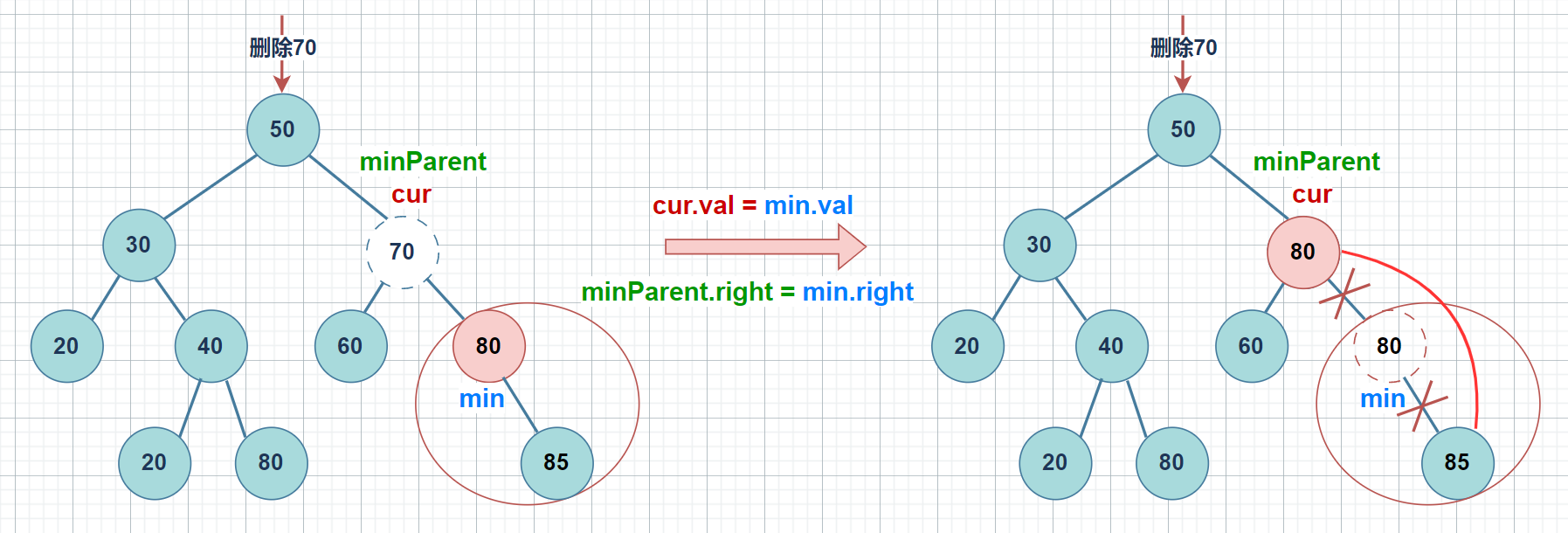
当右树根结点没有左孩子，那么 minParent.right 是右子树的最小值

最终实现代码：

private void removeNode(TreeNode cur, TreeNode parent) {
    if (cur.left == null) {
        // 1.如果待删除结点左孩子为空
        if (cur == root) {
            //左孩子为空的前提下，cur为根节点
            cur = cur.right;
        } else if (parent.left == cur) {
            //左孩子为空的前提下，cur为父节点的左树
            parent.left = cur.right;
        } else {
            //左孩子为空的前提下，cur为父节点的右树
            parent.right = cur.right;
        }
    } else if (cur.right == null) {
        // 2.如果待删除结点右孩子为空
        if (cur == root) {
            //右孩子为空的前提下，cur为根节点
            cur = cur.left;
        } else if (parent.left == cur) {
            //右孩子为空的前提下，cur为父节点的左树
            parent.left = cur.left;
        } else {
            //右孩子为空的前提下，cur为父节点的右树
            parent.right = cur.left;
        }
    } else {
        // 3.如果待删除结点左右孩子都不为空

        //这里是cur.left!=null && cur.right!=null的情况
        //替换删除：（找到右树里的最小值替换删除/找到左树的最大值替换删除）
        //下面展示找到右树里的最小值替换删除
        TreeNode minParent = cur;
        TreeNode min = cur.right;
        while (min.left != null) {
            minParent = min;
            min = min.left;
        }
        //此时 min 的左边一定为空
        //值替换
        cur.val = min.val;
        if (minParent.right == min) {
            // 当右树根结点没有左孩子，那么 minParent.right 是右子树的最小值
            minParent.right = min.right;
        } else {
            // 当右子树的根节点有左孩子，那么 minParent.left 是右子树的最小值
            minParent.left = min.right;
        }
    }
}