引言

深度学习处理文本主要涉及到自然语言处理（NLP）领域。随着深度学习技术的发展，NLP领域已经取得了很大的进展。以下是深度学习在处理文本中的一些主要应用和技术：

1. 词嵌入（Word Embeddings）: 词嵌入是将词汇表中的单词映射到稠密的向量，常用的方法有Word2Vec, GloVe和FastText。这些向量捕获单词之间的语义相似性。
2. 循环神经网络（RNN）: RNN是一种处理序列数据（如文本）的神经网络结构。它通过保存前一时间步的状态来捕获序列中的时间依赖关系。
3. 长短时记忆网络（LSTM）和门控循环单元（GRU）: 由于RNNs的短期记忆问题，LSTM和GRU被引入以捕获长距离的依赖关系。
4. Transformer 结构: 引入了自注意力机制的Transformer结构，如BERT, GPT, T5等模型，已经在多个NLP任务上取得了当前的最佳表现。
5. 序列到序列模型（Seq2Seq）: 这种模型常用于机器翻译、文本摘要等任务，通常与LSTM或Transformer结构一起使用。
6. 卷积神经网络（CNN）: 尽管CNN主要用于图像处理，但它也可以用于捕获文本中的局部模式。例如，用于情感分析和文本分类任务。
7. 迁移学习: 通过预先训练的模型（例如BERT），我们可以轻松地微调特定任务，从而减少训练时间和数据需求。
8. 注意力机制: 注意力机制使模型能够关注输入序列的特定部分，这在机器翻译和文本摘要等任务中特别有用。

处理文本的常见应用包括：文本分类、情感分析、命名实体识别、文本摘要、机器翻译、问答系统等。

为了在深度学习模型中使用文本，通常首先需要进行预处理，如分词、词干提取、去除停用词、转换为词嵌入等。然后，这些预处理后的文本数据可以作为深度学习模型的输入。

1. 反向传播

1.1 实例流程实现

1.2 前向传播

• 从输入层开始，传递数据通过每一层。
• 在每一层，使用当前的权重计算节点的输出。
• 这些输出成为下一层的输入。

1.3 计算损失

• 一旦数据通过所有层并生成了输出，就可以计算损失函数（如均方误差）来衡量网络预测的准确性。

1.4 反向传播误差

• 计算输出层误差，并将其反向传播到前面的层。
• 使用链式法则计算每一层的误差。

1.5 更新权重

• 使用学习率和之前计算的梯度来调整每一层的权重。
• 基本公式为: Δw=−η⋅∇J，其中 η 是学习率，∇J 是损失函数 J 关于权重 w 的梯度。

1.6 迭代

• 重复以上步骤多次，直到损失收敛到一个最小值或满足其他停止标准。

反向传播的核心是通过链式法则来计算损失函数相对于每个权重的偏导数。这些偏导数提供了权重应该如何调整的方向以减少误差。

为了实现反向传播，通常使用优化算法，如梯度下降或其变体（如随机梯度下降、Adam、RMSprop等），来更新网络中的权重。

1.7 BackPropagation & Adam 代码实例

#coding:utf8

import torch
import torch.nn as nn
import numpy as np
import copy

"""
基于pytorch的网络编写
手动实现梯度计算和反向传播
加入激活函数
"""

class TorchModel(nn.Module):
    def __init__(self, hidden_size):
        super(TorchModel, self).__init__()
        self.layer = nn.Linear(hidden_size, hidden_size, bias=False)
        self.activation = torch.sigmoid
        self.loss = nn.functional.mse_loss  #loss采用均方差损失

    #当输入真实标签，返回loss值；无真实标签，返回预测值
    def forward(self, x, y=None):
        y_pred = self.layer(x)
        y_pred = self.activation(y_pred)
        if y is not None:
            return self.loss(y_pred, y)
        else:
            return y_pred


#自定义模型，接受一个参数矩阵作为入参
class DiyModel:
    def __init__(self, weight):
        self.weight = weight

    def forward(self, x, y=None):
        x = np.dot(x, self.weight.T)
        y_pred = self.diy_sigmoid(x)
        if y is not None:
            return self.diy_mse_loss(y_pred, y)
        else:
            return y_pred

    #sigmoid
    def diy_sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    #手动实现mse，均方差loss
    def diy_mse_loss(self, y_pred, y_true):
        return np.sum(np.square(y_pred - y_true)) / len(y_pred)

    #手动实现梯度计算
    def calculate_grad(self, y_pred, y_true, x):
        #前向过程
        # wx = np.dot(self.weight, x)
        # sigmoid_wx = self.diy_sigmoid(wx)
        # loss = self.diy_mse_loss(sigmoid_wx, y_true)
        #反向过程
        # 均方差函数 (y_pred - y_true) ^ 2 / n 的导数 = 2 * (y_pred - y_true) / n , 结果为2维向量
        grad_mse = 2/len(x) * (y_pred - y_true)
        # sigmoid函数 y = 1/(1+e^(-x)) 的导数 = y * (1 - y), 结果为2维向量
        grad_sigmoid = y_pred * (1 - y_pred)
        # wx矩阵运算，见ppt拆解, wx = [w11*x0 + w21*x1, w12*x0 + w22*x1]
        #导数链式相乘
        grad_w11 = grad_mse[0] * grad_sigmoid[0] * x[0]
        grad_w12 = grad_mse[1] * grad_sigmoid[1] * x[0]
        grad_w21 = grad_mse[0] * grad_sigmoid[0] * x[1]
        grad_w22 = grad_mse[1] * grad_sigmoid[1] * x[1]
        grad = np.array([[grad_w11, grad_w12],
                         [grad_w21, grad_w22]])
        #由于pytorch存储做了转置，输出时也做转置处理
        return grad.T

#梯度更新
def diy_sgd(grad, weight, learning_rate):
    return weight - learning_rate * grad

#adam梯度更新
def diy_adam(grad, weight):
    #参数应当放在外面，此处为保持后方代码整洁简单实现一步
    alpha = 1e-3  #学习率
    beta1 = 0.9   #超参数
    beta2 = 0.999 #超参数
    eps = 1e-8    #超参数
    t = 0         #初始化
    mt = 0        #初始化
    vt = 0        #初始化
    #开始计算
    t = t + 1
    gt = grad
    mt = beta1 * mt + (1 - beta1) * gt
    vt = beta2 * vt + (1 - beta2) * gt ** 2
    mth = mt / (1 - beta1 ** t)
    vth = vt / (1 - beta2 ** t)
    weight = weight - (alpha / (np.sqrt(vth) + eps)) * mth
    return weight

x = np.array([-0.5, 0.1])  #输入
y = np.array([0.1, 0.2])  #预期输出

#torch实验
torch_model = TorchModel(2)
torch_model_w = torch_model.state_dict()["layer.weight"]
print(torch_model_w, "初始化权重")
numpy_model_w = copy.deepcopy(torch_model_w.numpy())
#numpy array -> torch tensor, unsqueeze的目的是增加一个batchsize维度
torch_x = torch.from_numpy(x).float().unsqueeze(0)
torch_y = torch.from_numpy(y).float().unsqueeze(0)
#torch的前向计算过程，得到loss
torch_loss = torch_model(torch_x, torch_y)
print("torch模型计算loss：", torch_loss)
# #手动实现loss计算
diy_model = DiyModel(numpy_model_w)
diy_loss = diy_model.forward(x, y)
print("diy模型计算loss：", diy_loss)

# #设定优化器
learning_rate = 0.1
optimizer = torch.optim.SGD(torch_model.parameters(), lr=learning_rate)
# optimizer = torch.optim.Adam(torch_model.parameters())
optimizer.zero_grad()
#
# #pytorch的反向传播操作
torch_loss.backward()
print(torch_model.layer.weight.grad, "torch 计算梯度")  #查看某层权重的梯度

# #手动实现反向传播
grad = diy_model.calculate_grad(diy_model.forward(x), y, x)
print(grad, "diy 计算梯度")
#
# #torch梯度更新
# optimizer.step()
# #查看更新后权重
# update_torch_model_w = torch_model.state_dict()["layer.weight"]
# print(update_torch_model_w, "torch更新后权重")
#
# #手动梯度更新
# diy_update_w = diy_sgd(grad, numpy_model_w, learning_rate)
# diy_update_w = diy_adam(grad, numpy_model_w)
# print(diy_update_w, "diy更新权重")

2. 优化器 – Adam

2.1 Adam解析

Adam (Adaptive Moment Estimation) 是一个广泛使用的优化算法，设计用于深度学习模型。它结合了两种其他的优化算法：Adagrad 和 RMSprop。

以下是 Adam 的特点和工作原理：

1. 动量：与传统的动量方法相似，Adam 使用移动平均来获得梯度的过去值。这帮助算法导航在相关的梯度下降方向，特别是在解决高度非凸的优化问题时。
2. 学习率自适应：与 RMSprop 和 Adagrad 一样，Adam 根据过去的平方梯度调整每个参数的学习率。这有助于算法在学习的早期快速前进，而在接近最小值时减速。

具体算法：

1. 初始化参数。
2. 计算梯度
3. 计算第一矩估计 mt
4. 计算第二矩估计 vt
5. 对mt和vt进行偏置校正
6. 更新权重

优点：
计算效率高。需要的内存小。适用于大多数深度学习应用。适用于非稳定的目标函数、大型问题、高噪声或稀疏梯度。

缺点：
Adam 可能需要更多的时候来收敛，尤其是在深度学习训练的后期。
对某些问题，它可能不如其他的算法（如 SGD 或 RMSprop）稳定。

2.2 代码实例

class AdamOptimizer:
    def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8):
        self.learning_rate = learning_rate
        self.beta1 = beta1
        self.beta2 = beta2
        self.epsilon = epsilon
        
        # 初始化一阶矩估计和二阶矩估计
        self.m = 0
        self.v = 0
        self.t = 0

    def step(self, gradient):
        self.t += 1  # 增加时间步

        # 更新偏差修正的一阶矩估计
        self.m = self.beta1 * self.m + (1 - self.beta1) * gradient

        # 更新偏差修正的二阶矩估计
        self.v = self.beta2 * self.v + (1 - self.beta2) * gradient**2

        # 计算偏差修正的一阶矩估计
        m_corr = self.m / (1 - self.beta1**self.t)

        # 计算偏差修正的二阶矩估计
        v_corr = self.v / (1 - self.beta2**self.t)

        # 更新参数
        update = self.learning_rate * m_corr / (v_corr**0.5 + self.epsilon)

        return update

3. NLP任务

自然语言处理（NLP, Natural Language Processing）是计算机科学、人工智能和语言学交叉的一个领域，它使机器能够读懂、解释、生成和相应人类语言。随着技术的进步，NLP任务变得越来越先进，并在许多实际应用中发挥了作用。

以下是一些主要的NLP任务：

1. 文本分类：将给定的文本归类到预定义的类别中。例如，情感分析（判断文本是正面的、负面的还是中立的）。
2. 命名实体识别 (NER)：从文本中识别出如人名、地名、机构名等特定类别的实体。
3. 词性标注：为文本中的每个词分配一个词性标签，如名词、动词、形容词等。
4. 句法分析：构建文本的句法结构，通常采用树状图来表示。
5. 语义角色标注：确定句子中每个成分的语义角色，如施事、受事等。
6. 语言模型：预测下一个词或字符的出现概率。这在许多应用中都很有用，如机器翻译和语音识别。
7. 机器翻译：将文本从一种语言翻译成另一种语言。
8. 问答系统：根据用户的问题从文档中提取或生成答案。
9. 文本生成：基于给定的输入生成新的文本。
   10.语音识别：将音频转换为文本。

现给定一个任务
任务：字符串分类 – 判断字符串中是否出现了指定字符
例：
指定字符：a
样本： abcd 正样本
bcde 负样本

4. 神经网络处理文本

任务
当前输入：字符串 如：abcd
预期输出：概率值 正样本=1，负样本=0，以0.5为分界
X = “abcd” Y = 1
X =“bcde” Y = 0

建模目标：找到一个映射f(x)，使得f(“abcd”) = 1, f(“bcde”) = 0

4.1 step1 字符数值化

直观方式，a -> 1, b -> 2, c -> 3 …. z -> 26 是否合理？
显然不够合理

每个字符转化成同维度向量
a - > [0.32618175 0.20962898 0.43550067 0.07120884 0.58215387]
b - > [0.21841921 0.97431001 0.43676452 0.77925024 0.7307891 ]
…
z -> [0.72847746 0.72803551 0.43888069 0.09266955 0.65148562]

那么“abcd” - > 4 * 5 的矩阵
[[0.32618175 0.20962898 0.43550067 0.07120884 0.58215387]
[0.21841921 0.97431001 0.43676452 0.77925024 0.7307891 ]
[0.95035602 0.45280039 0.06675379 0.72238734 0.02466642]
[0.86751814 0.97157839 0.0127658 0.98910503 0.92606296]]
矩阵形状 = 文本长度 * 向量长度

4.2 step 2 矩阵转化为向量

求平均
[[0.32618175 0.20962898 0.43550067 0.07120884 0.58215387]
[0.21841921 0.97431001 0.43676452 0.77925024 0.7307891 ]
[0.95035602 0.45280039 0.06675379 0.72238734 0.02466642]
[0.86751814 0.97157839 0.0127658 0.98910503 0.92606296]]
->
[0.59061878 0.65207944 0.2379462 0.64048786 0.56591809]
由4 * 5 矩阵 -> 1* 5 向量 形状 = 1*向量长度

4.3 step 3 向量到数值

采取最简单的线性公式 y = w * x + b
w 维度为1*向量维度 b为实数
例：
w = [1, 1], b = -1, x = [1,2]

4.4 step 4 数值归一化

sigmoid函数
x = 3 σ(x) = 0.9526

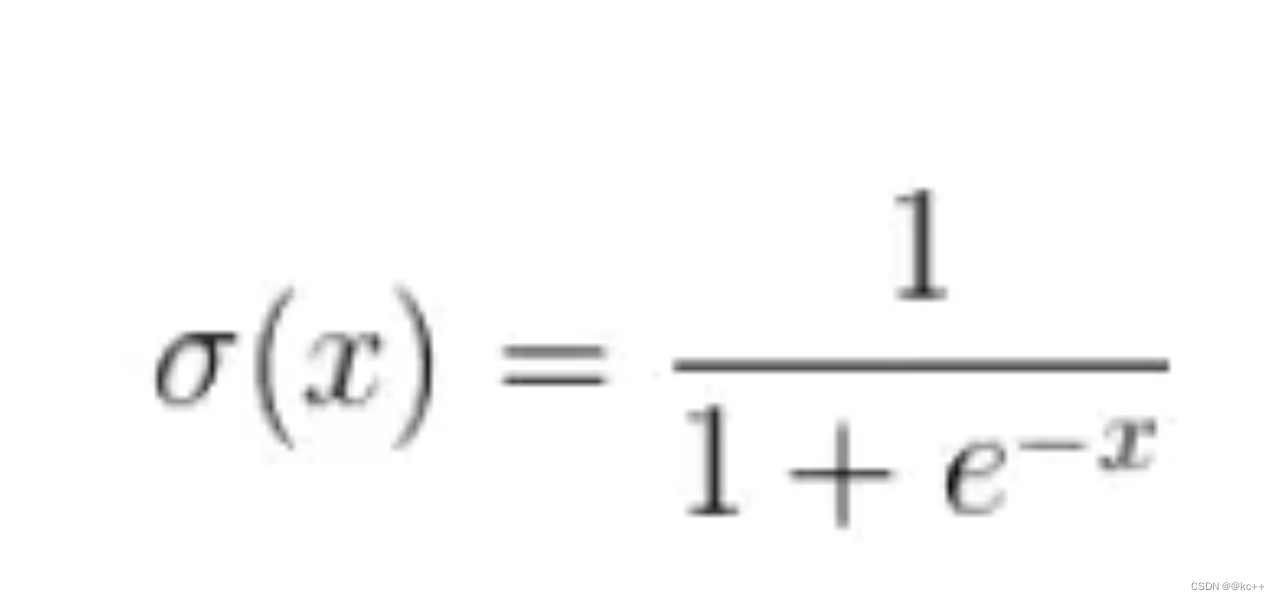
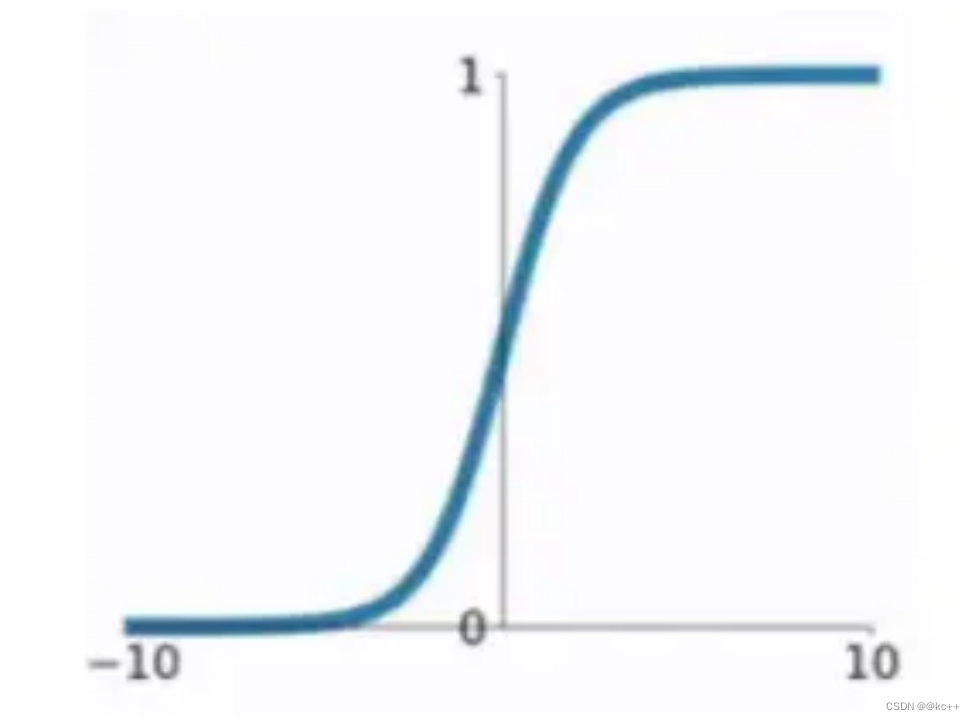
4.5 总结

整体映射
“abcd” ----每个字符转化成向量----> 4 * 5矩阵
4 * 5矩阵 ----向量求平均----> 1 * 5向量
1 * 5向量 ----w*x + b线性公式 —> 实数
实数 ----sigmoid归一化函数—> 0-1之间实数

黄色部分需要通过训练优化

5. Embedding层

5.1 解析

Embedding层在神经网络中用于将离散型数据（通常是文本数据的整数标识）转换为持续型向量表示，也就是词嵌入。这一层通常用于自然语言处理（NLP）任务，例如文本分类、情感分析或机器翻译等。

在嵌入层中，每个唯一的标识（比如一个词的整数ID）都会映射到一个固定大小的向量。这些向量通过模型的训练进行优化，以便更好地完成给定任务。

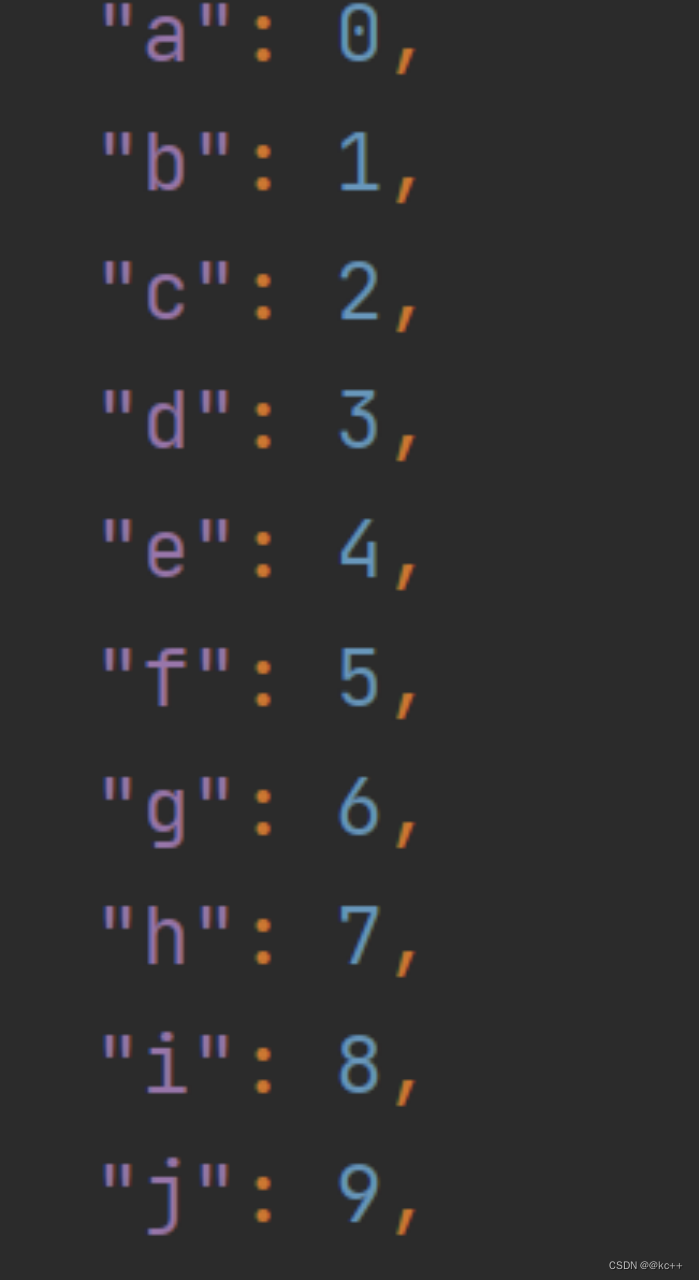
搭配词表文件
对于中文通常使用字
对于英文使用token
多个语种和符号可以出现在同一份词表中
目的：“abc" --词表–> 0,1,2 --Embedding层–> 3*n的矩阵 --model–>

5.2 代码实例

#coding:utf8
import torch
import torch.nn as nn

'''
embedding层的处理
'''

num_embeddings = 6  #通常对于nlp任务，此参数为字符集字符总数
embedding_dim = 5   #每个字符向量化后的向量维度
embedding_layer = nn.Embedding(num_embeddings, embedding_dim)
print(embedding_layer.weight, "随机初始化权重")

#构造输入
x = torch.LongTensor([[1,2,3],[2,2,0]])
embedding_out = embedding_layer(x)
print(embedding_out)

6. 网络结构 – 全连接层

网络结构-全连接层
又称线性层
计算公式：y = w * x + b
W和b是参与训练的参数
W的维度决定了隐含层输出的维度，一般称为隐单元个数（hidden size）
举例：
输入：x （维度1 x 3）
隐含层1：w（维度3 x 5）
隐含层2: w（维度5 x 2）

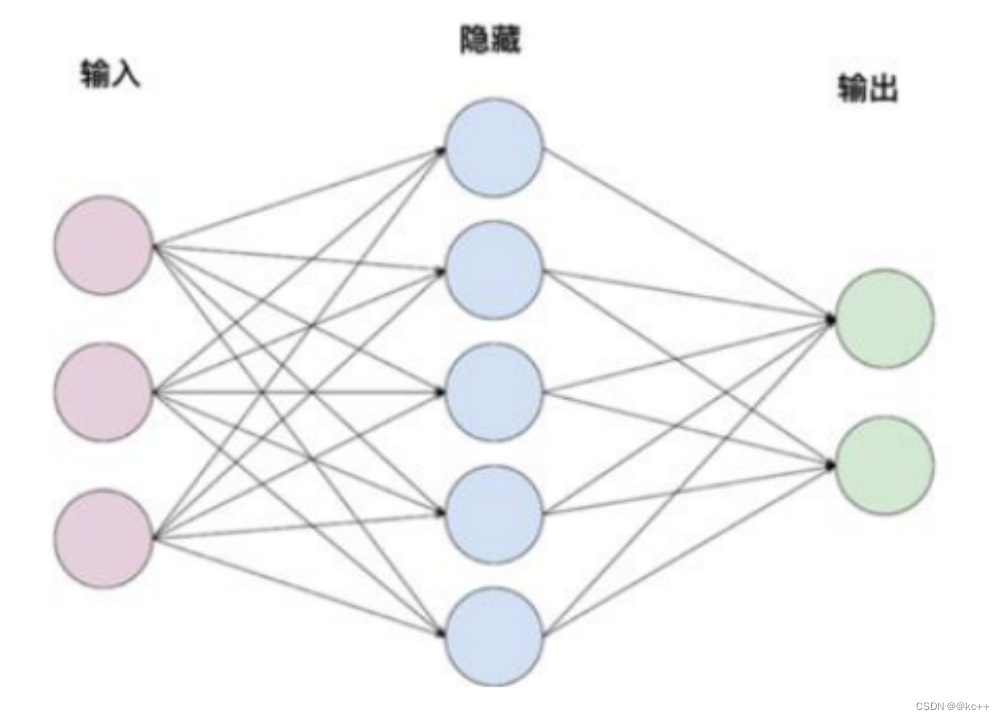
7. 网络结构 – RNN

7.1 解析

循环神经网络（Recurrent Neural Networks, RNN）是一种用于处理序列数据的神经网络结构。与传统的前馈神经网络不同，RNN具有记忆功能，能够保存前一步或多步的信息。这使得RNN特别适合处理如时间序列数据、文本、语音等依赖于前文信息的任务。

在RNN中，神经元不仅接收新的输入，还维持一种状态（通常用隐藏层表示），该状态在网络的每一步迭代中都会更新。简单地说，RNN每次接收一个输入并生成一个输出，同时更新其内部状态。

RNN的一个典型应用是自然语言处理（NLP），例如文本生成、文本分类和机器翻译。然而，由于梯度消失或梯度爆炸问题，基础的RNN结构在处理长序列时可能会遇到困难。为了解决这些问题，更复杂的RNN变体如长短时记忆（LSTM）和门控循环单元（GRU）被开发出来。

循环神经网络（recurrent neural network）
主要思想：将整个序列划分成多个时间步，将每一个时间步的信息依次输入模型，同时将模型输出的结果传给下一个时间步

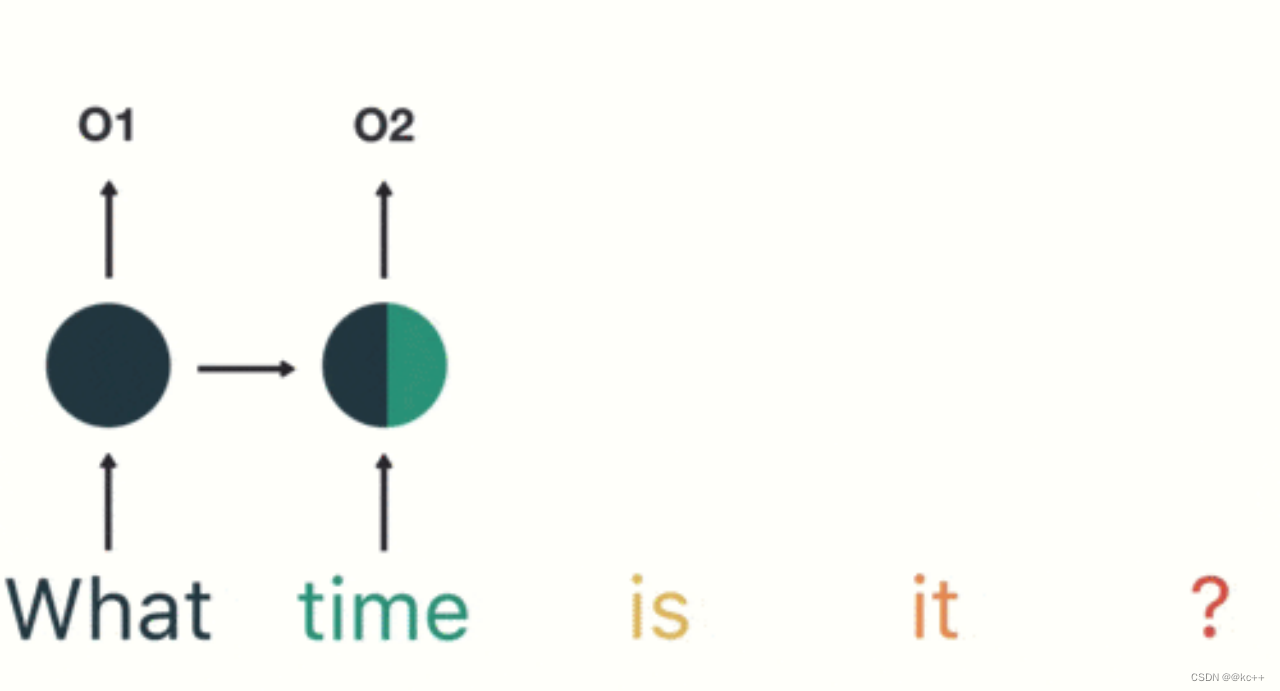
公式：

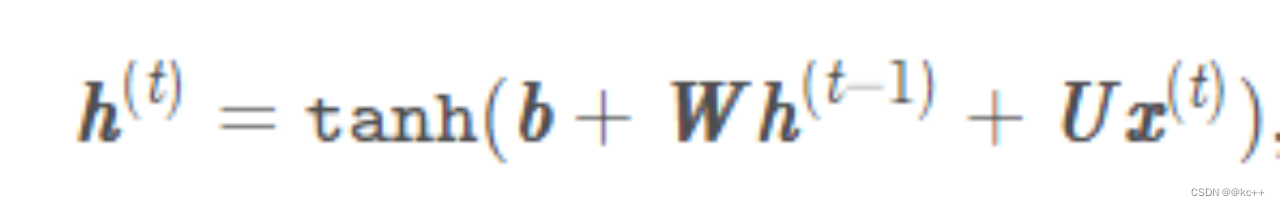
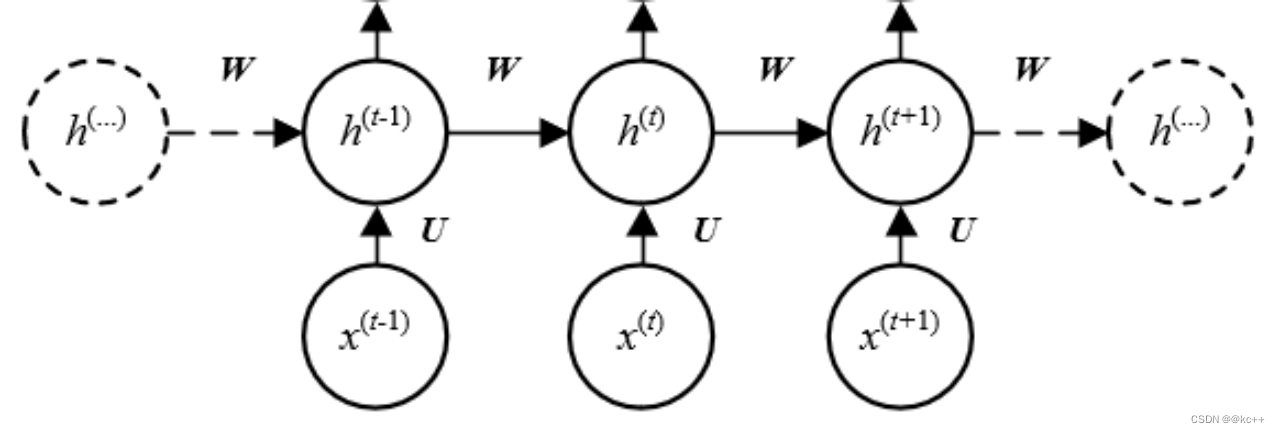
7.2 代码实例

#coding:utf8

import torch
import torch.nn as nn
import numpy as np


"""
手动实现简单的神经网络
使用pytorch实现RNN
手动实现RNN
对比
"""

class TorchRNN(nn.Module):
    def __init__(self, input_size, hidden_size):
        super(TorchRNN, self).__init__()
        self.layer = nn.RNN(input_size, hidden_size, bias=False, batch_first=True)

    def forward(self, x):
        return self.layer(x)

#自定义RNN模型
class DiyModel:
    def __init__(self, w_ih, w_hh, hidden_size):
        self.w_ih = w_ih
        self.w_hh = w_hh
        self.hidden_size = hidden_size

    def forward(self, x):
        ht = np.zeros((self.hidden_size))
        output = []
        for xt in x:
            ux = np.dot(self.w_ih, xt)
            wh = np.dot(self.w_hh, ht)
            ht_next = np.tanh(ux + wh)
            output.append(ht_next)
            ht = ht_next
        return np.array(output), ht


x = np.array([[1, 2, 3],
              [3, 4, 5],
              [5, 6, 7]])  #网络输入

#torch实验
hidden_size = 4
torch_model = TorchRNN(3, hidden_size)
# print(torch_model.state_dict())
w_ih = torch_model.state_dict()["layer.weight_ih_l0"]
w_hh = torch_model.state_dict()["layer.weight_hh_l0"]
print(w_ih, w_ih.shape)
print(w_hh, w_hh.shape)
#
torch_x = torch.FloatTensor([x])
output, h = torch_model.forward(torch_x)
print(h)
print(output.detach().numpy(), "torch模型预测结果")
print(h.detach().numpy(), "torch模型预测隐含层结果")
print("---------------")
diy_model = DiyModel(w_ih, w_hh, hidden_size)
output, h = diy_model.forward(x)
print(output, "diy模型预测结果")
print(h, "diy模型预测隐含层结果")

8. 网络结构 – CNN

8.1 解析

以卷积操作为基础的网络结构，每个卷积核可以看成一个特征提取器

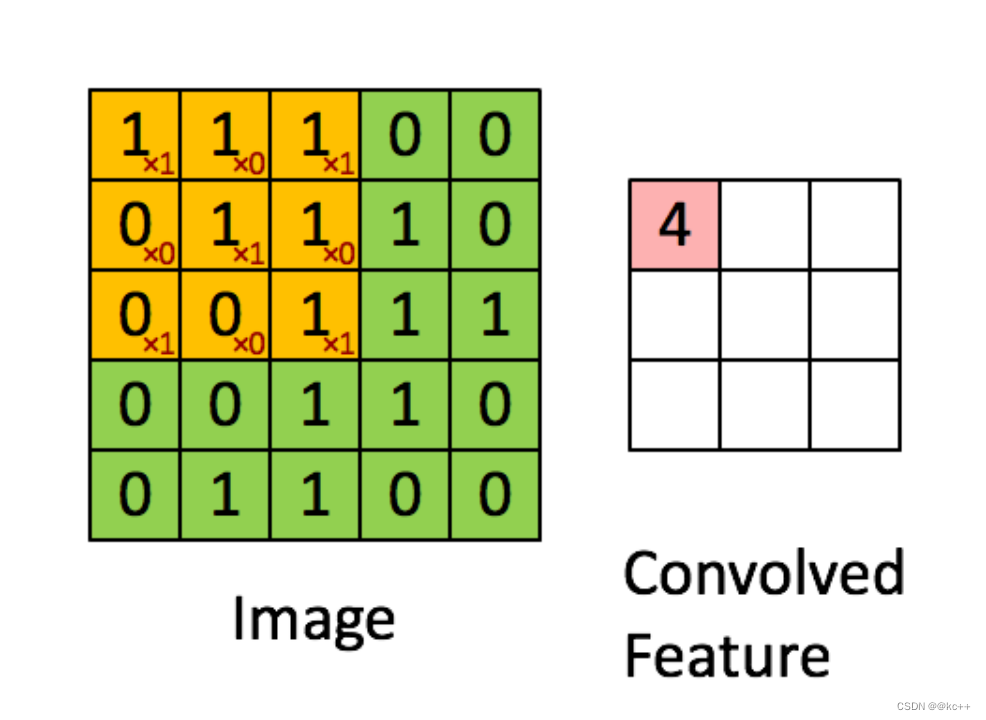
8.2 代码实例

#coding:utf8

import torch
import torch.nn as nn
import numpy as np


"""
手动实现简单的神经网络
使用pytorch实现CNN
手动实现CNN
对比
"""
#一个二维卷积
class TorchCNN(nn.Module):
    def __init__(self, in_channel, out_channel, kernel):
        super(TorchCNN, self).__init__()
        self.layer = nn.Conv2d(in_channel, out_channel, kernel, bias=False)

    def forward(self, x):
        return self.layer(x)

#自定义CNN模型
class DiyModel:
    def __init__(self, input_height, input_width, weights, kernel_size):
        self.height = input_height
        self.width = input_width
        self.weights = weights
        self.kernel_size = kernel_size

    def forward(self, x):
        output = []
        for kernel_weight in self.weights:
            kernel_weight = kernel_weight.squeeze().numpy() #shape : 2x2
            kernel_output = np.zeros((self.height - kernel_size + 1, self.width - kernel_size + 1))
            for i in range(self.height - kernel_size + 1):
                for j in range(self.width - kernel_size + 1):
                    window = x[i:i+kernel_size, j:j+kernel_size]
                    kernel_output[i, j] = np.sum(kernel_weight * window) # np.dot(a, b) != a * b
            output.append(kernel_output)
        return np.array(output)


x = np.array([[0.1, 0.2, 0.3, 0.4],
              [-3, -4, -5, -6],
              [5.1, 6.2, 7.3, 8.4],
              [-0.7, -0.8, -0.9, -1]])  #网络输入

#torch实验
in_channel = 1
out_channel = 3
kernel_size = 2
torch_model = TorchCNN(in_channel, out_channel, kernel_size)
print(torch_model.state_dict())
torch_w = torch_model.state_dict()["layer.weight"]
# print(torch_w.numpy().shape)
torch_x = torch.FloatTensor([[x]])
output = torch_model.forward(torch_x)
output = output.detach().numpy()
print(output, output.shape, "torch模型预测结果\n")
print("---------------")
diy_model = DiyModel(x.shape[0], x.shape[1], torch_w, kernel_size)
output = diy_model.forward(x)
print(output, "diy模型预测结果")

#######################

#一维卷积层，在nlp中更加常用
kernel_size = 3
input_dim = 5
hidden_size = 4
torch_cnn1d = nn.Conv1d(input_dim, hidden_size, kernel_size)
# for key, weight in torch_cnn1d.state_dict().items():
#     print(key, weight.shape)

def numpy_cnn1d(x, state_dict):
    weight = state_dict["weight"].numpy()
    bias = state_dict["bias"].numpy()
    sequence_output = []
    for i in range(0, x.shape[1] - kernel_size + 1):
        window = x[:, i:i+kernel_size]
        kernel_outputs = []
        for kernel in weight:
            kernel_outputs.append(np.sum(kernel * window))
        sequence_output.append(np.array(kernel_outputs) + bias)
    return np.array(sequence_output).T

# x = torch.from_numpy(np.random.random((length, input_dim)))
# x = x.transpose(1, 0)
# print(torch_cnn1d(torch.Tensor([x])))
# print(numpy_cnn1d(x, torch_cnn1d.state_dict()))

9. 网络结构 – LSTM

9.1 解析

将RNN的隐单元复杂化一定程度规避了梯度消失和信息遗忘的问题

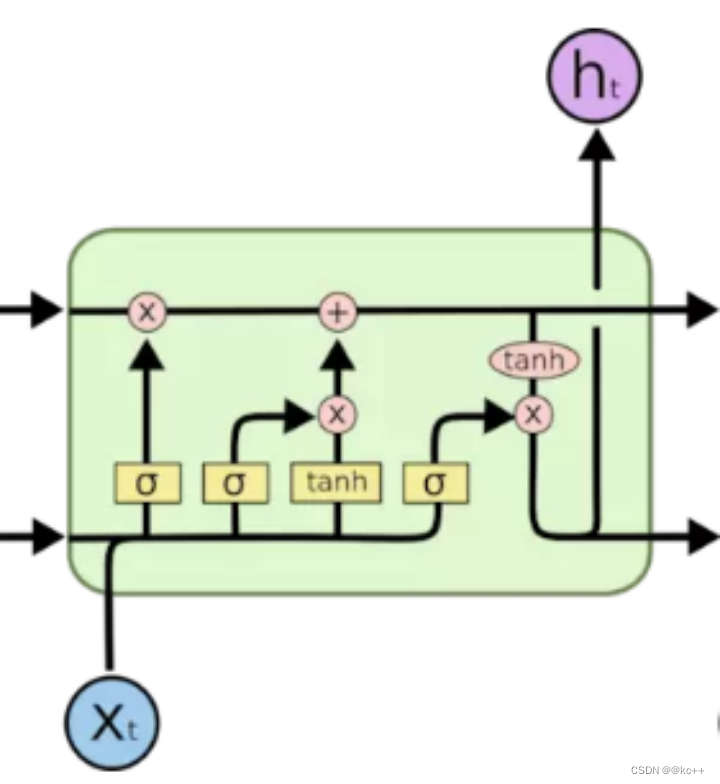
长短时记忆（Long Short-Term Memory, LSTM）网络是一种特殊类型的循环神经网络（RNN），旨在解决基础RNN在处理长序列时可能出现的梯度消失或梯度爆炸问题。LSTM由Sepp Hochreiter和Jürgen Schmidhuber于1997年首次提出，并已被广泛用于各种涉及序列数据的任务，如自然语言处理、语音识别和时间序列预测。

LSTM的核心思想是引入了“记忆单元”（cell）和三个“门”（gate）：输入门、输出门和遗忘门。这些门和记忆单元共同作用，以决定如何更新网络的状态。

1. 输入门：决定新输入的哪些部分需要更新记忆状态。
2. 遗忘门：决定哪些旧信息需要被遗忘或保留。
3. 输出门：基于当前的输入和记忆单元，决定输出什么信息。

这三个门的结构使LSTM能够在长序列中更有效地捕获依赖关系。

9.2 代码实例

import torch
import torch.nn as nn
import numpy as np

'''
用矩阵运算的方式复现一些基础的模型结构
清楚模型的计算细节，有助于加深对于模型的理解，以及模型转换等工作
'''

#构造一个输入
length = 6
input_dim = 12
hidden_size = 7
x = np.random.random((length, input_dim))
# print(x)

#使用pytorch的lstm层
torch_lstm = nn.LSTM(input_dim, hidden_size, batch_first=True)
for key, weight in torch_lstm.state_dict().items():
    print(key, weight.shape)

def sigmoid(x):
    return 1/(1 + np.exp(-x))

#将pytorch的lstm网络权重拿出来，用numpy通过矩阵运算实现lstm的计算
def numpy_lstm(x, state_dict):
    weight_ih = state_dict["weight_ih_l0"].numpy()
    weight_hh = state_dict["weight_hh_l0"].numpy()
    bias_ih = state_dict["bias_ih_l0"].numpy()
    bias_hh = state_dict["bias_hh_l0"].numpy()
    #pytorch将四个门的权重拼接存储，我们将它拆开
    w_i_x, w_f_x, w_c_x, w_o_x = weight_ih[0:hidden_size, :], \
                                 weight_ih[hidden_size:hidden_size*2, :],\
                                 weight_ih[hidden_size*2:hidden_size*3, :],\
                                 weight_ih[hidden_size*3:hidden_size*4, :]
    w_i_h, w_f_h, w_c_h, w_o_h = weight_hh[0:hidden_size, :], \
                                 weight_hh[hidden_size:hidden_size * 2, :], \
                                 weight_hh[hidden_size * 2:hidden_size * 3, :], \
                                 weight_hh[hidden_size * 3:hidden_size * 4, :]
    b_i_x, b_f_x, b_c_x, b_o_x = bias_ih[0:hidden_size], \
                                 bias_ih[hidden_size:hidden_size * 2], \
                                 bias_ih[hidden_size * 2:hidden_size * 3], \
                                 bias_ih[hidden_size * 3:hidden_size * 4]
    b_i_h, b_f_h, b_c_h, b_o_h = bias_hh[0:hidden_size], \
                                 bias_hh[hidden_size:hidden_size * 2], \
                                 bias_hh[hidden_size * 2:hidden_size * 3], \
                                 bias_hh[hidden_size * 3:hidden_size * 4]
    w_i = np.concatenate([w_i_h, w_i_x], axis=1)
    w_f = np.concatenate([w_f_h, w_f_x], axis=1)
    w_c = np.concatenate([w_c_h, w_c_x], axis=1)
    w_o = np.concatenate([w_o_h, w_o_x], axis=1)
    b_f = b_f_h + b_f_x
    b_i = b_i_h + b_i_x
    b_c = b_c_h + b_c_x
    b_o = b_o_h + b_o_x
    c_t = np.zeros((1, hidden_size))
    h_t = np.zeros((1, hidden_size))
    sequence_output = []
    for x_t in x:
        x_t = x_t[np.newaxis, :]
        hx = np.concatenate([h_t, x_t], axis=1)
        # f_t = sigmoid(np.dot(x_t, w_f_x.T) + b_f_x + np.dot(h_t, w_f_h.T) + b_f_h)
        f_t = sigmoid(np.dot(hx, w_f.T) + b_f)
        # i_t = sigmoid(np.dot(x_t, w_i_x.T) + b_i_x + np.dot(h_t, w_i_h.T) + b_i_h)
        i_t = sigmoid(np.dot(hx, w_i.T) + b_i)
        # g = np.tanh(np.dot(x_t, w_c_x.T) + b_c_x + np.dot(h_t, w_c_h.T) + b_c_h)
        g = np.tanh(np.dot(hx, w_c.T) + b_c)
        c_t = f_t * c_t + i_t * g
        # o_t = sigmoid(np.dot(x_t, w_o_x.T) + b_o_x + np.dot(h_t, w_o_h.T) + b_o_h)
        o_t = sigmoid(np.dot(hx, w_o.T) + b_o)
        h_t = o_t * np.tanh(c_t)
        sequence_output.append(h_t)
    return np.array(sequence_output), (h_t, c_t)


# torch_sequence_output, (torch_h, torch_c) = torch_lstm(torch.Tensor([x]))
# numpy_sequence_output, (numpy_h, numpy_c) = numpy_lstm(x, torch_lstm.state_dict())
#
# print(torch_sequence_output)
# print(numpy_sequence_output)
# print("--------")
# print(torch_h)
# print(numpy_h)
# print("--------")
# print(torch_c)
# print(numpy_c)

#############################################################

#使用pytorch的GRU层
torch_gru = nn.GRU(input_dim, hidden_size, batch_first=True)
# for key, weight in torch_gru.state_dict().items():
#     print(key, weight.shape)


#将pytorch的GRU网络权重拿出来，用numpy通过矩阵运算实现GRU的计算
def numpy_gru(x, state_dict):
    weight_ih = state_dict["weight_ih_l0"].numpy()
    weight_hh = state_dict["weight_hh_l0"].numpy()
    bias_ih = state_dict["bias_ih_l0"].numpy()
    bias_hh = state_dict["bias_hh_l0"].numpy()
    #pytorch将3个门的权重拼接存储，我们将它拆开
    w_r_x, w_z_x, w_x = weight_ih[0:hidden_size, :], \
                        weight_ih[hidden_size:hidden_size * 2, :],\
                        weight_ih[hidden_size * 2:hidden_size * 3, :]
    w_r_h, w_z_h, w_h = weight_hh[0:hidden_size, :], \
                        weight_hh[hidden_size:hidden_size * 2, :], \
                        weight_hh[hidden_size * 2:hidden_size * 3, :]
    b_r_x, b_z_x, b_x = bias_ih[0:hidden_size], \
                        bias_ih[hidden_size:hidden_size * 2], \
                        bias_ih[hidden_size * 2:hidden_size * 3]
    b_r_h, b_z_h, b_h = bias_hh[0:hidden_size], \
                        bias_hh[hidden_size:hidden_size * 2], \
                        bias_hh[hidden_size * 2:hidden_size * 3]
    w_z = np.concatenate([w_z_h, w_z_x], axis=1)
    w_r = np.concatenate([w_r_h, w_r_x], axis=1)
    b_z = b_z_h + b_z_x
    b_r = b_r_h + b_r_x
    h_t = np.zeros((1, hidden_size))
    sequence_output = []
    for x_t in x:
        x_t = x_t[np.newaxis, :]
        hx = np.concatenate([h_t, x_t], axis=1)
        z_t = sigmoid(np.dot(hx, w_z.T) + b_z)
        r_t = sigmoid(np.dot(hx, w_r.T) + b_r)
        h = np.tanh(r_t * (np.dot(h_t, w_h.T) + b_h) + np.dot(x_t, w_x.T) + b_x)
        h_t = (1 - z_t) * h + z_t * h_t
        sequence_output.append(h_t)
    return np.array(sequence_output), h_t

# torch_sequence_output, torch_h = torch_gru(torch.Tensor([x]))
# numpy_sequence_output, numpy_h = numpy_gru(x, torch_gru.state_dict())
#
# print(torch_sequence_output)
# print(numpy_sequence_output)
# print("--------")
# print(torch_h)
# print(numpy_h)

10. 网络结构 – GRU

10.1 解析

LSTM的一种简化变体
在不同任务上与LSTM效果各有优劣

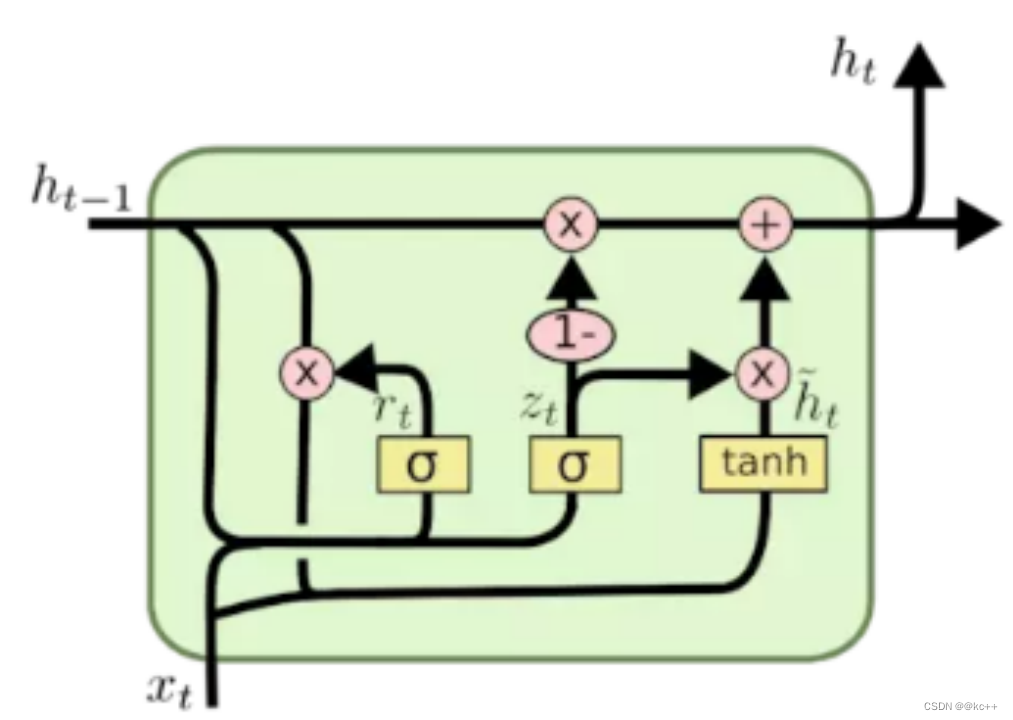
门控循环单元（Gated Recurrent Unit, GRU）是一种循环神经网络（RNN）的变体，由Kyunghyun Cho等人在2014年提出。GRU旨在解决标准RNN结构在处理长序列时面临的梯度消失问题，与长短时记忆（LSTM）网络有相似的目的。

与LSTM相比，GRU有更简单的结构，主要由两个门组成：

1. 更新门（Update Gate）：决定哪些信息从前一状态传递到当前状态。
2. 重置门（Reset Gate）：决定哪些过去的信息会与当前的输入一起用于更新当前状态。

因为GRU有更少的门和参数，所以它们通常更快地训练，尤其是在不需要捕获极长依赖关系的数据集上。

10.2 代码实例

import torch
import torch.nn as nn

# 定义模型结构
class GRUModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(GRUModel, self).__init__()
        self.gru = nn.GRU(input_dim, hidden_dim, batch_first=True)
        self.fc = nn.Linear(hidden_dim, output_dim)
        
    def forward(self, x):
        out, _ = self.gru(x)
        out = self.fc(out[:, -1, :])
        return out

# 参数设置
input_dim = 64  # 输入的特征维度
hidden_dim = 50  # GRU层的隐藏状态维度
output_dim = 1   # 输出层的维度（用于二分类）

# 初始化模型、损失函数和优化器
model = GRUModel(input_dim, hidden_dim, output_dim)
criterion = nn.BCEWithLogitsLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

# 假设我们有一个形状为(batch_size, seq_len, input_dim)的输入数据和相应的标签
# 这里我们仅用随机数据作为例子
batch_size = 32
seq_len = 10
x = torch.randn(batch_size, seq_len, input_dim)
y = torch.randint(0, 2, (batch_size, output_dim), dtype=torch.float32)

# 前向传播
outputs = model(x)

# 计算损失
loss = criterion(outputs, y)

# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()

11. 网络结构 – TextCNN

11.1 解析

利用一维卷积对文本进行编码编码后的文本矩阵通过pooling转化为向量，用于分类

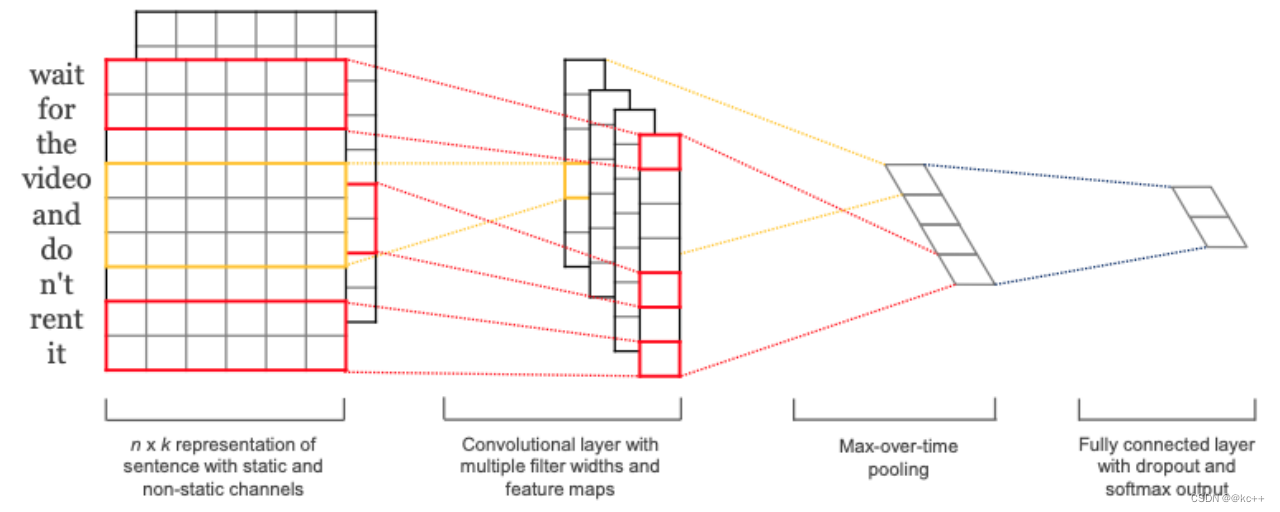
11.2 代码实例

import torch
import torch.nn as nn
import torch.nn.functional as F

# 定义TextCNN模型
class TextCNN(nn.Module):
    def __init__(self, vocab_size, embed_dim, num_classes, kernel_sizes=[3, 4, 5], num_filters=100):
        super(TextCNN, self).__init__()
        
        # 嵌入层
        self.embedding = nn.Embedding(vocab_size, embed_dim)
        
        # 卷积层
        self.convs = nn.ModuleList([
            nn.Conv1d(in_channels=embed_dim, out_channels=num_filters, kernel_size=k)
            for k in kernel_sizes
        ])
        
        # 全连接层
        self.fc = nn.Linear(len(kernel_sizes) * num_filters, num_classes)

    def forward(self, x):
        # 输入x形状：[批量大小, 序列长度]
        
        # 嵌入
        x = self.embedding(x)  # 输出形状：[批量大小, 序列长度, 嵌入维度]
        
        # Conv1D期望输入形状：[批量大小, 嵌入维度, 序列长度]
        x = x.permute(0, 2, 1)
        
        # 卷积
        x = [F.relu(conv(x)) for conv in self.convs]
        
        # 池化
        x = [F.max_pool1d(c, c.size(-1)).squeeze(-1) for c in x]
        
        # 拼接
        x = torch.cat(x, 1)
        
        # 全连接层
        x = self.fc(x)
        
        return x

# 超参数
vocab_size = 5000  # 词汇表大小
embed_dim = 300  # 嵌入维度
num_classes = 2  # 类别数
kernel_sizes = [3, 4, 5]  # 卷积核大小
num_filters = 100  # 卷积核数量

# 初始化模型
model = TextCNN(vocab_size, embed_dim, num_classes, kernel_sizes, num_filters)

# 示例输入（在实际应用中，这应是预处理并编码为整数的文本序列）
# 输入形状：[批量大小, 序列长度]
input_batch = torch.randint(0, vocab_size, (32, 50))

# 前向传播
output = model(input_batch)

12. 池化层

12.1 解析

• 降低了后续网络层的输入维度，缩减模型大小，提高计算速度
• 提高了Feature Map 的鲁棒性，防止过拟合
  

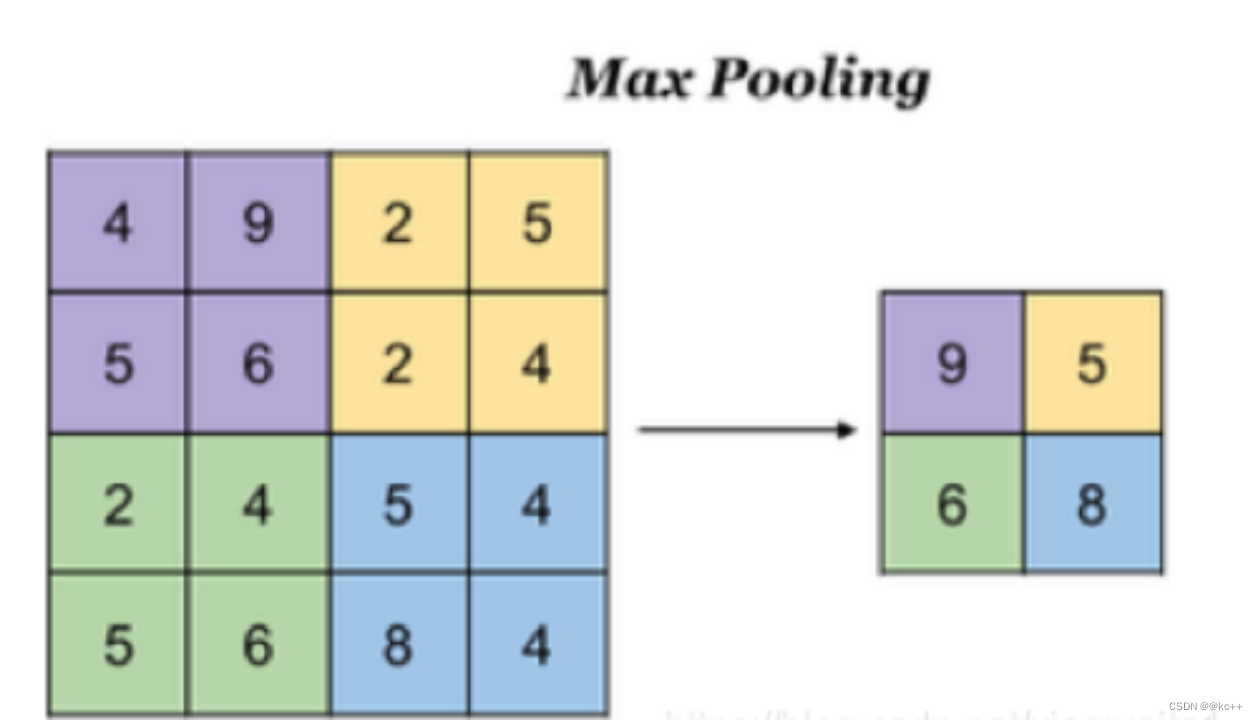
12.2 代码实例

#coding:utf8
import torch
import torch.nn as nn

'''
pooling层的处理
'''

#pooling操作默认对于输入张量的最后一维进行
#入参5，代表把五维池化为一维
layer = nn.AvgPool1d(5)
#随机生成一个维度为3x4x5的张量
#可以想象成3条,文本长度为4,向量长度为5的样本
x = torch.rand([3, 4, 5])
print(x)
print(x.shape)
#经过pooling层
y = layer(x)
print(y)
print(y.shape)
#squeeze方法去掉值为1的维度
y = y.squeeze()
print(y)
print(y.shape)

13. Normalization

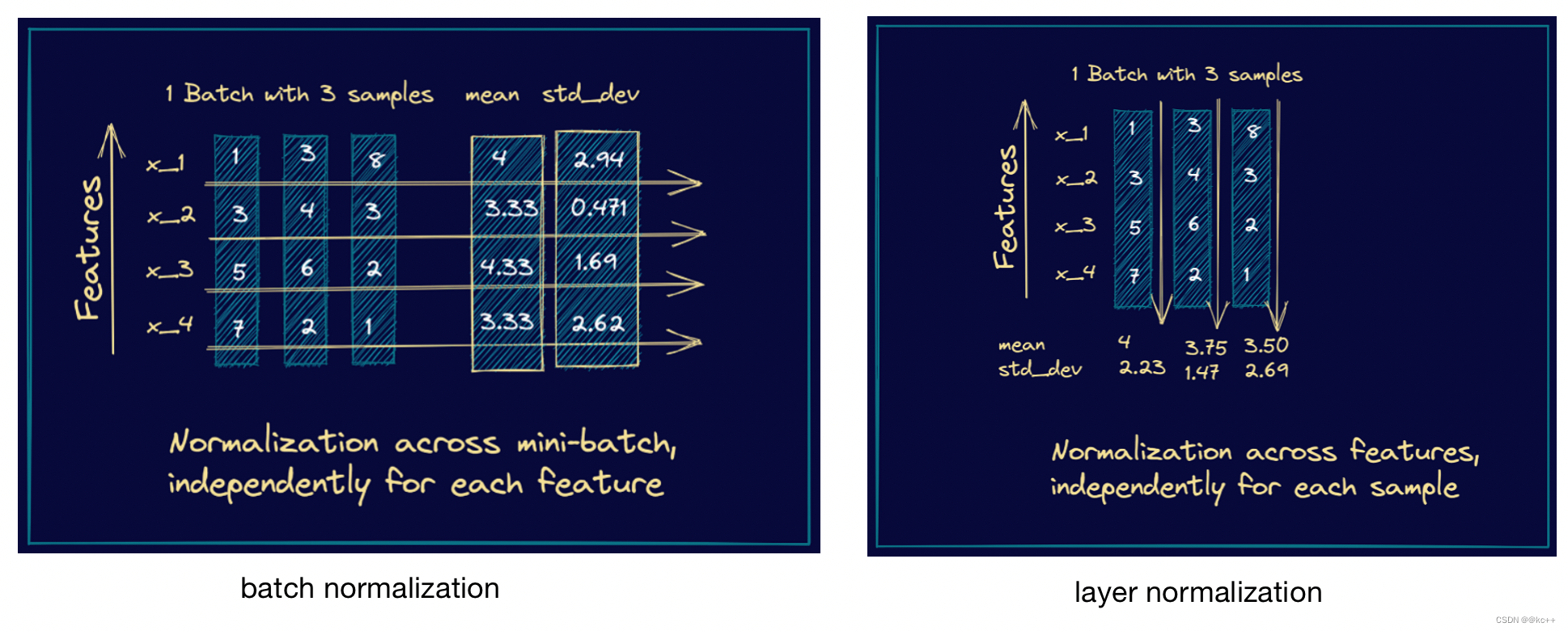
标准化是机器学习和统计中用于缩放特征的技术，使它们具有可比性和可解释性。常见的标准化方法有最小-最大标准化（Min-Max Normalization）和Z分数标准化（Z-score Normalization，也叫标准化）。

标准化的好处

1. 加速训练：标准化数据在训练过程中更快地收敛。
2. 特征可比：使不同的特征具有可比性。
3. 有助于某些算法：例如k-NN和SVM等依赖于数据点之间的距离，标准化在这些情况下是有帮助的。

14. Dropout层

14.1 解析

• 作用：减少过拟合
• 按照指定概率，随机丢弃一些神经元（将其化为零）
• 其余元素乘以 1 / (1 – p)进行放大

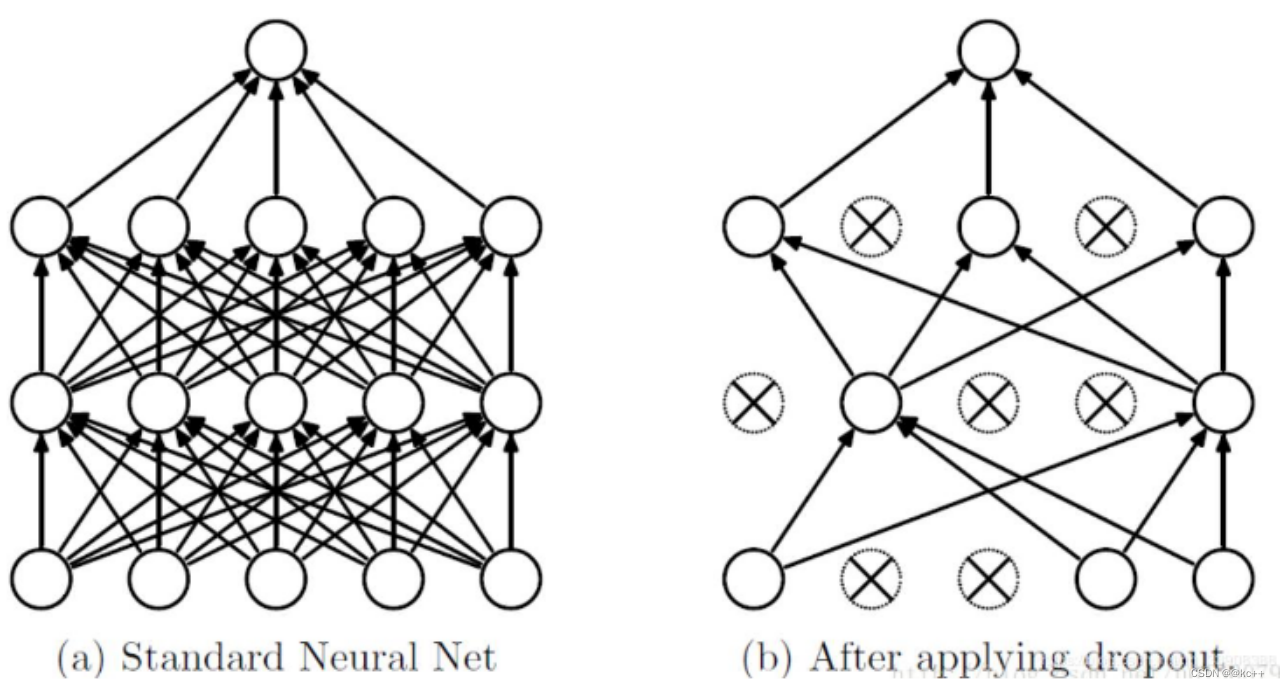
• 如何理解其作用
• 强迫一个神经单元，和随机挑选出来的其他神经单元共同工作，消除减弱了神经元节点间的联合适应性，增强了泛化能力
• 可以看做是一种模型平均，由于每次随机忽略的隐层节点都不同，这样就使每次训练的网络都是不一样的，每次训练都可以单做一个“新”的模型
• 启示：计算方式并不是越复杂就越好

14.2 代码实例

#coding:utf8

import torch
import torch.nn as nn
import numpy as np


"""
基于pytorch的网络编写
测试dropout层
"""

import torch

x = torch.Tensor([1,2,3,4,5,6,7,8,9])
dp_layer = torch.nn.Dropout(0.5)
dp_x = dp_layer(x)
print(dp_x)