目录
8.11二叉树展开为链表(中等)
8.12从前序与中序遍历序列构造二叉树(中等)
8.13路径总和III(中等)
8.14二叉树的最近公共祖先(中等)
8.15二叉树中的最大路径和(困难)
8.11二叉树展开为链表(中等)
题目描述:leetcode链接 114. 二叉树展开为链表
给你二叉树的根结点
root,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。- 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
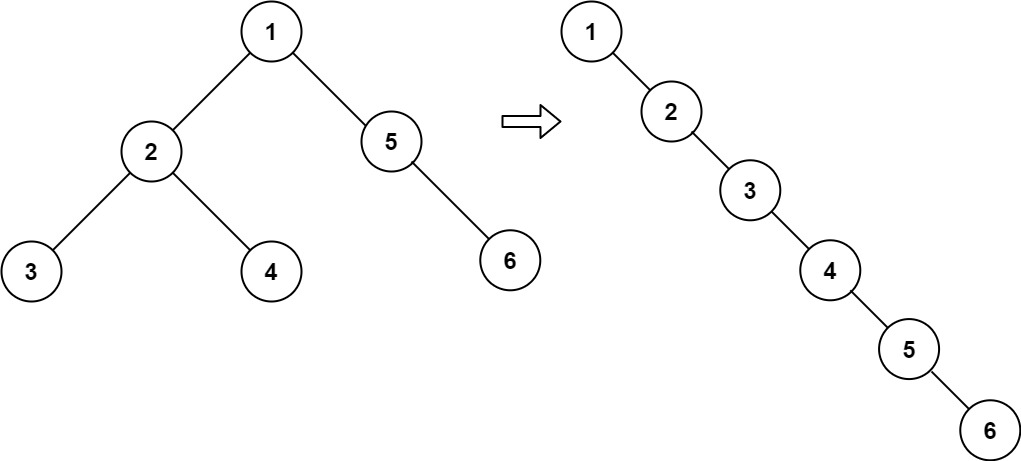
输入:root = [1,2,5,3,4,null,6] 输出:[1,null,2,null,3,null,4,null,5,null,6]示例 2:
输入:root = [] 输出:[]示例 3:
输入:root = [0] 输出:[0]
思路:

1.将左、右子树分别变为链表L和R
2.根节点的右节点变为L的根节点,根节点的左节点为空
3.L尾节点的右节点变为R的根节点
举例说明:
见上图
代码:
class Solution {
public:
void flatten(TreeNode* root) {
if (!root) return;
flatten(root -> left);
flatten(root -> right);
TreeNode* temp = root -> right;
root -> right = root -> left;
root -> left = nullptr;
while(root -> right) root = root -> right;
root -> right = temp;
}
};8.12从前序与中序遍历序列构造二叉树(中等)
题目描述:leetcode链接 105. 从前序与中序遍历序列构造二叉树
给定两个整数数组
preorder和inorder,其中preorder是二叉树的先序遍历,inorder是同一棵树的中序遍历,请构造二叉树并返回其根节点。示例 1:
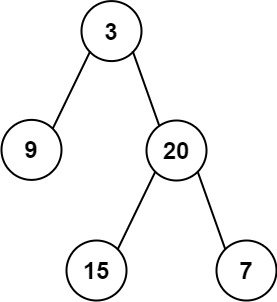
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]
思路:

1.由于前序遍历的顺序是【根-左子树-右子树】,中序遍历的顺序是【左子树-根-右子树】,所以由上图的前序遍历preorder可知,它的第一个元素3为根节点。那么由中序遍历inorder可知根节点3的左侧元素为左子树,共1个元素;根节点3的右侧元素为右子树,共3个元素。
2.记录3的左子树的前序遍历顺序和中序遍历顺序,其中9即为3的左节点
记录3的右子树的前序遍历顺序和中序遍历顺序,其中20即为3的右节点
3.记录20的左子树的前序遍历顺序和中序遍历顺序,其中15即为20的左节点
记录20的右子树的前序遍历顺序和中序遍历顺序,其中7即为20的右节点
举例说明:
见上图
代码:
class Solution {
public:
unordered_map<int, int> mp;
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
for (int i = 0; i < n; i++) {
mp[inorder[i]] = i;
}
return build(preorder, inorder, 0, n - 1, 0, n - 1);
}
TreeNode* build(vector<int>& preorder, vector<int>& inorder, int pre_l, int pre_r, int in_l, int in_r) {
if (pre_l > pre_r) return nullptr;
//前序遍历中的根节点位置
int pre_root = pre_l;
//中序遍历中的根节点位置
int in_root = mp[preorder[pre_root]];
TreeNode* root = new TreeNode(preorder[pre_root]);
//左子树节点个数
int size_l = in_root - in_l;
//构造左右子树
root -> left = build(preorder, inorder, pre_root + 1, pre_root + size_l, in_l, in_root - 1);
root -> right = build(preorder, inorder, pre_root + size_l + 1, pre_r, in_root + 1, in_r);
return root;
}
};8.13路径总和III(中等)
题目描述:leetcode链接 437. 路径总和 III
给定一个二叉树的根节点
root,和一个整数targetSum,求该二叉树里节点值之和等于targetSum的 路径 的数目。路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
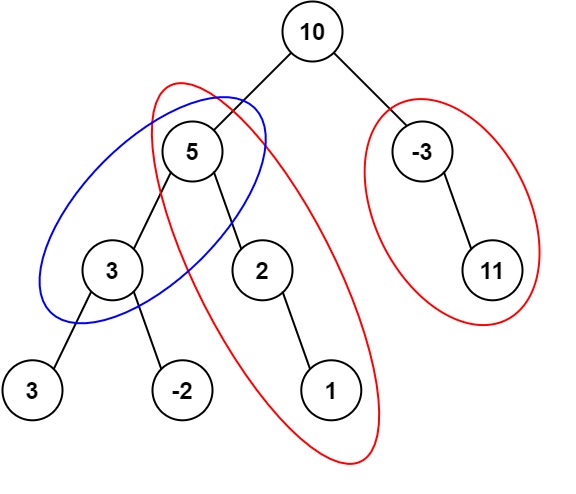
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3
思路:
和560. 和为K的子数组类似,使用前缀和+哈希表的方式来解决,只不过我们现在面对的数据是存储在二叉树里面了
注:unordered_map<long, int> mp和long sum的类型为long,要不然有几个测试用例通过不了
举例说明:
无
代码:
class Solution {
public:
int ans = 0;
unordered_map<long, int> mp;
int pathSum(TreeNode* root, int targetSum) {
mp[0] = 1;
dfs(root, targetSum, 0);
return ans;
}
void dfs(TreeNode* root, int targetSum, long sum) {
if (!root) return;
sum += root -> val;
if (mp.find(sum - targetSum) != mp.end()) ans += mp[sum - targetSum];
mp[sum]++;
dfs(root -> left, targetSum, sum);
dfs(root -> right, targetSum, sum);
mp[sum]--;
}
};8.14二叉树的最近公共祖先(中等)
题目描述:leetcode链接 236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
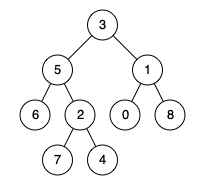
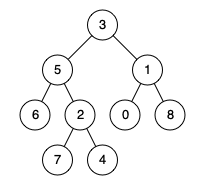
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点5和节点1的最近公共祖先是节点3示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点5和节点4的最近公共祖先是节点5。因为根据定义最近公共祖先节点可以为节点本身。示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1
思路:
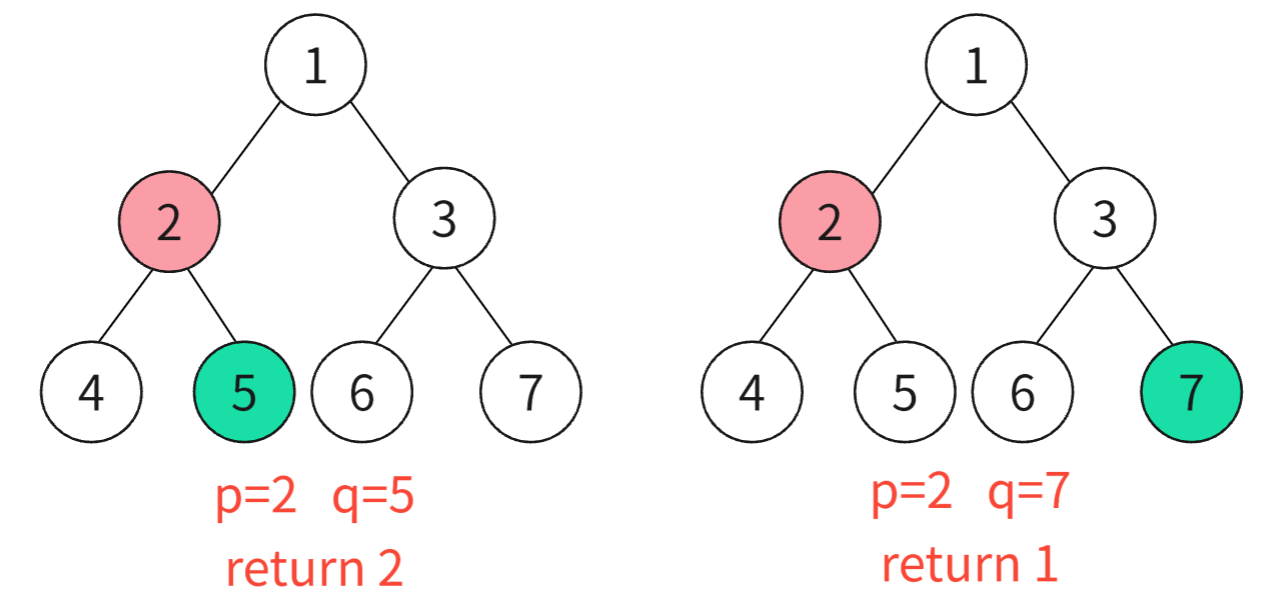
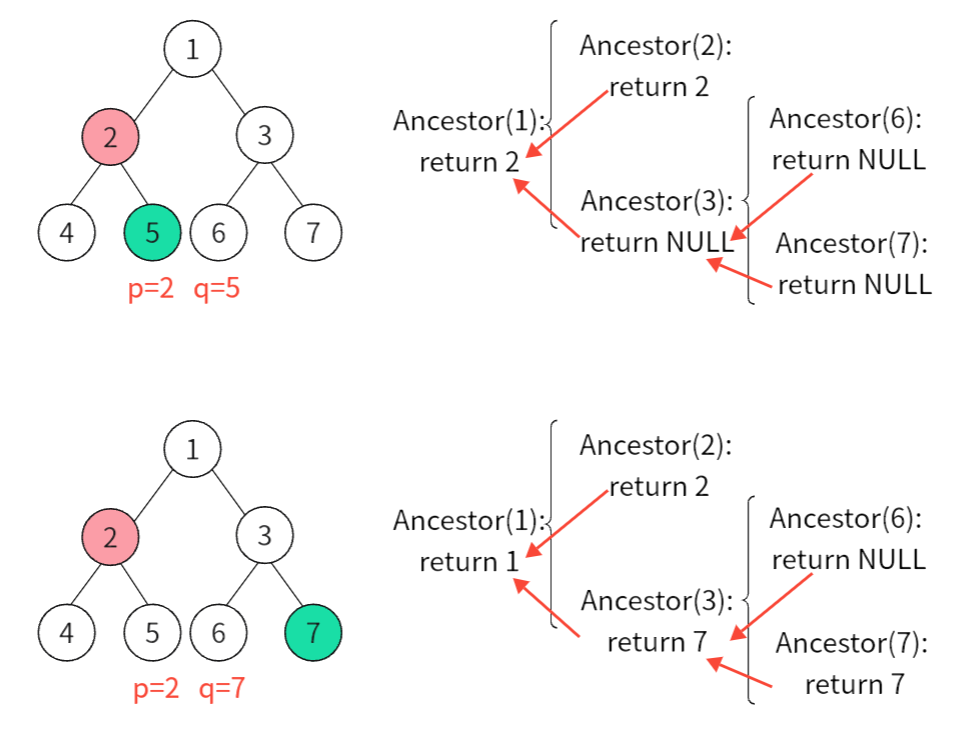
按照p、q中一节点是否是另一节点的祖先节点可以分为上图两种情况 。
使用递归,分以下几种情况讨论:
1.如果当前节点为空,或者等于p,或者等于q,返回当前节点
2.如果当前节点左、右子树均不返回空,返回当前节点
3.如果当前节点左子树返回不为空,右子树为空,返回左子树递归结果
4.如果当前节点右子树返回不为空,左子树为空,返回右子树递归结果
5.如果当前节点左、右子树均返回空,返回空
举例说明:
代码:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (!root || root == p || root == q) {
return root;
}
TreeNode* L = lowestCommonAncestor(root -> left, p, q);
TreeNode* R = lowestCommonAncestor(root -> right, p, q);
if (L && R) return root;
return L ? L : R;
}
};
8.15二叉树中的最大路径和(困难)
题目描述:leetcode链接 199. 二叉树中的最大路径和
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点
root,返回其 最大路径和 。示例 1:
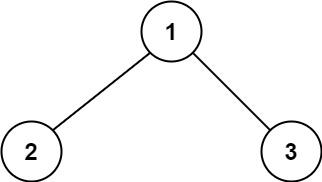
输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6示例 2:
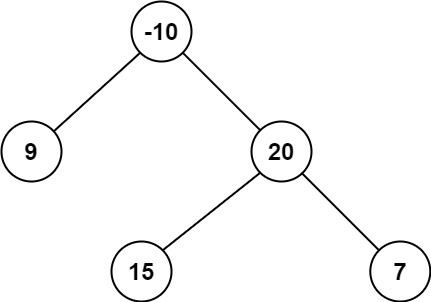
输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
思路:
1.定义一个函数getNum(TreeNode* root),可以计算root节点的贡献值
贡献值可以理解为以该节点为起点,在其子树中寻找一条路径,使其路径和最大
对空节点而言,getNum(NULL)=0
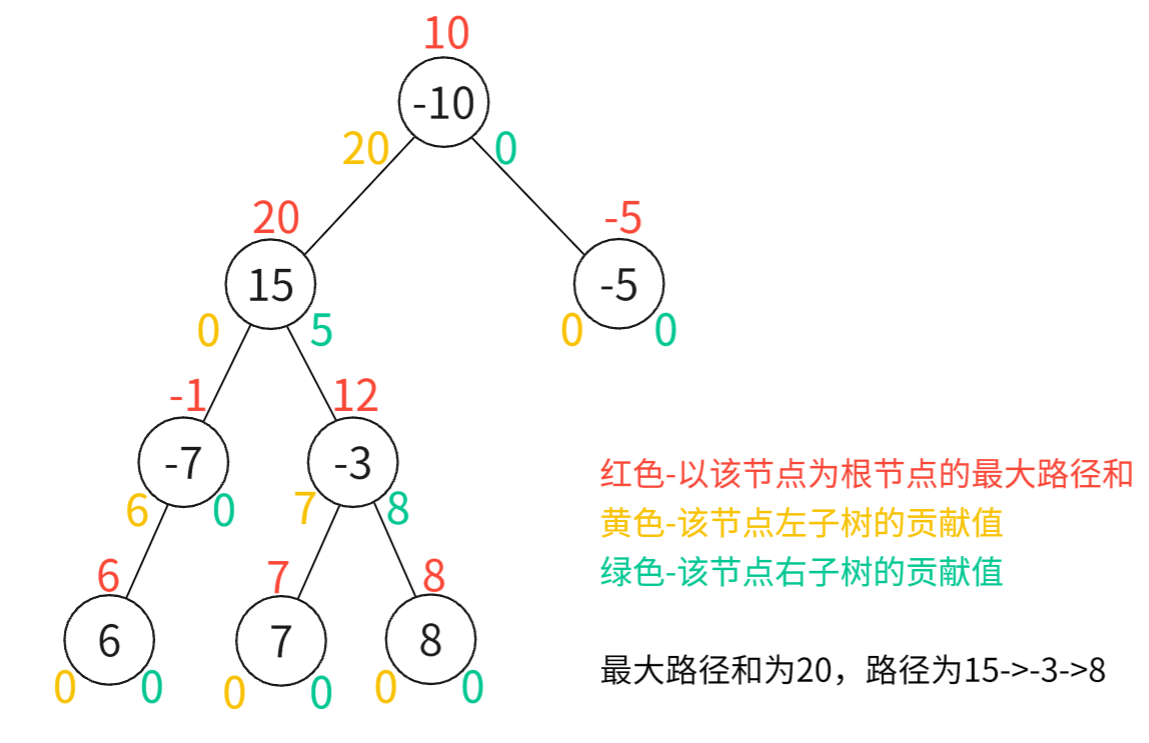
2.以下图为例,
根节点-10的路径和ans(-10)= -10+max(getNum(15), 0)+max(getNum(-5), 0)
遍历所有节点,其中ans的最大值即为二叉树的最大路径和
举例说明:
代码:
class Solution {
public:
int ans = INT_MIN;
int maxPathSum(TreeNode* root) {
getNum(root);
return ans;
}
int getNum(TreeNode* root){
if (!root) return 0;
int L = max(getNum(root -> left), 0);
int R = max(getNum(root -> right), 0);
ans = max(ans, root -> val + L + R);
return root -> val + max(L, R);
}
};