1.题目描述
这里有一幅服务器分布图，服务器的位置标识在 m * n 的整数矩阵网格 grid 中，1 表示单元格上有服务器，0 表示没有。

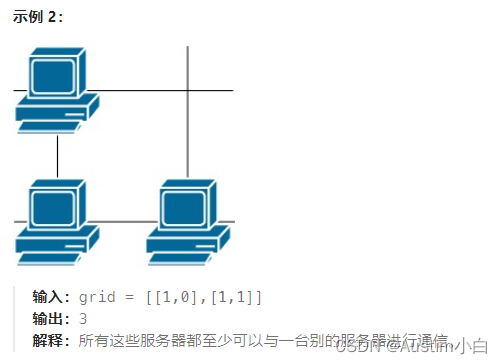
如果两台服务器位于同一行或者同一列，我们就认为它们之间可以进行通信。

请你统计并返回能够与至少一台其他服务器进行通信的服务器的数量。

我们可以使用两次遍历解决本题。

在第一次遍历中，我们遍历数组 grid\textit{grid}grid，如果 grid[i,j]\textit{grid}[i, j]grid[i,j] 的值为 111，说明位置 (i,j)(i, j)(i,j) 有一台服务器，我们可以将第 iii 行服务器的数量，以及第 jjj 行服务器的数量，均加上 111。为了维护行列中服务器的数量，我们可以使用两个哈希映射 row\textit{row}row 和 col\textit{col}col，row\textit{row}row 中存储行的编号以及每一行服务器的数量，col\textit{col}col 存储列的编号以及每一列服务器的数量。

在第二次遍历中，我们就可以根据 row\textit{row}row 和 col\textit{col}col 来判断每一台服务器是否能与至少其它一台服务器进行通信了。如果 grid(i,j)\textit{grid}(i, j)grid(i,j) 的值为 111，并且 row[i]\textit{row}[i]row[i] 和 col[j]\textit{col}[j]col[j] 中至少有一个严格大于 111，就说明位置 (i,j)(i, j)(i,j) 的服务器能与同一行或者同一列的另一台服务器进行通信，答案加 111。

int countServers(int** grid, int gridSize, int* gridColSize){
    int m = gridSize, n = gridColSize[0];
    int rows[m];
    int cols[n];
    //置0
    memset(rows, 0, sizeof(rows));
    memset(cols, 0, sizeof(cols));

    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == 1) {
                rows[i]++;
                cols[j]++;
            }
        }
    }
    int ans = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (grid[i][j] == 1 && (rows[i] > 1 || cols[j] > 1)) {
                ans++;
            }
        }
    }
    return ans;

}