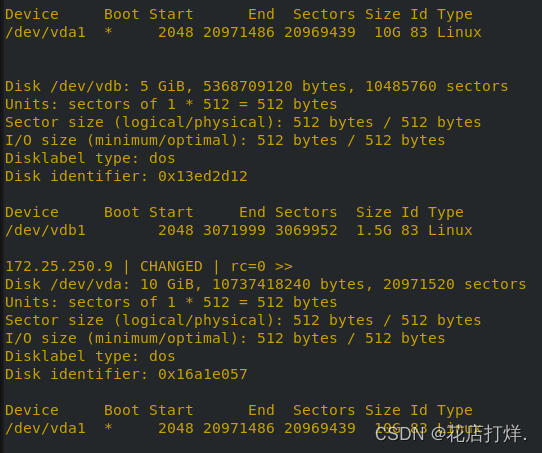
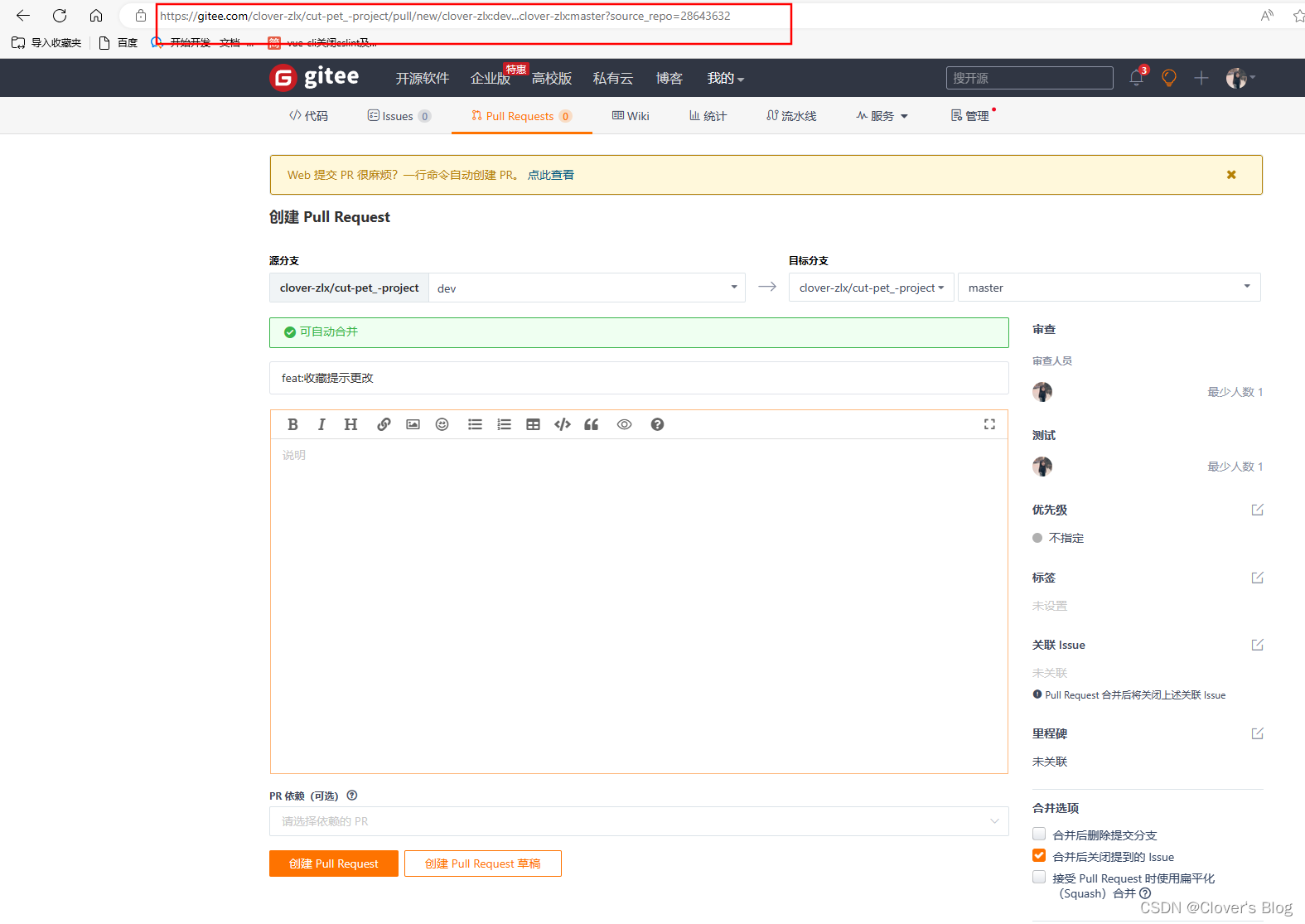
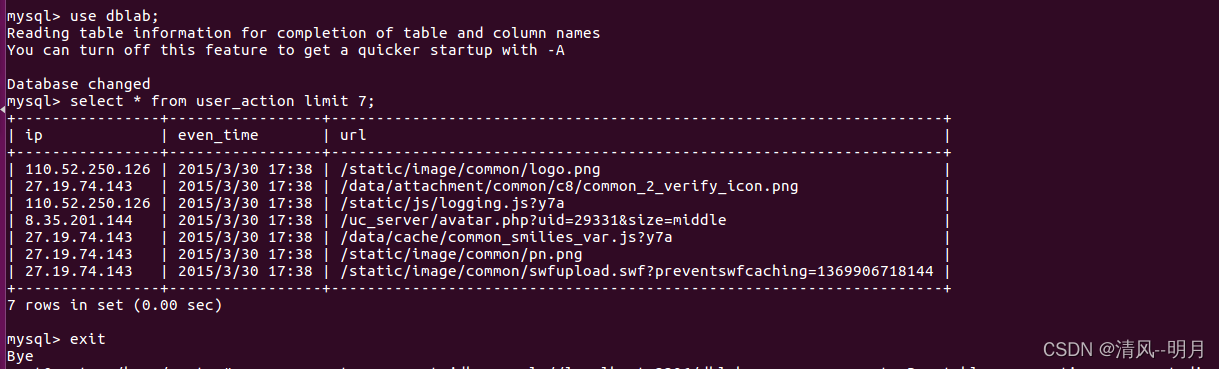
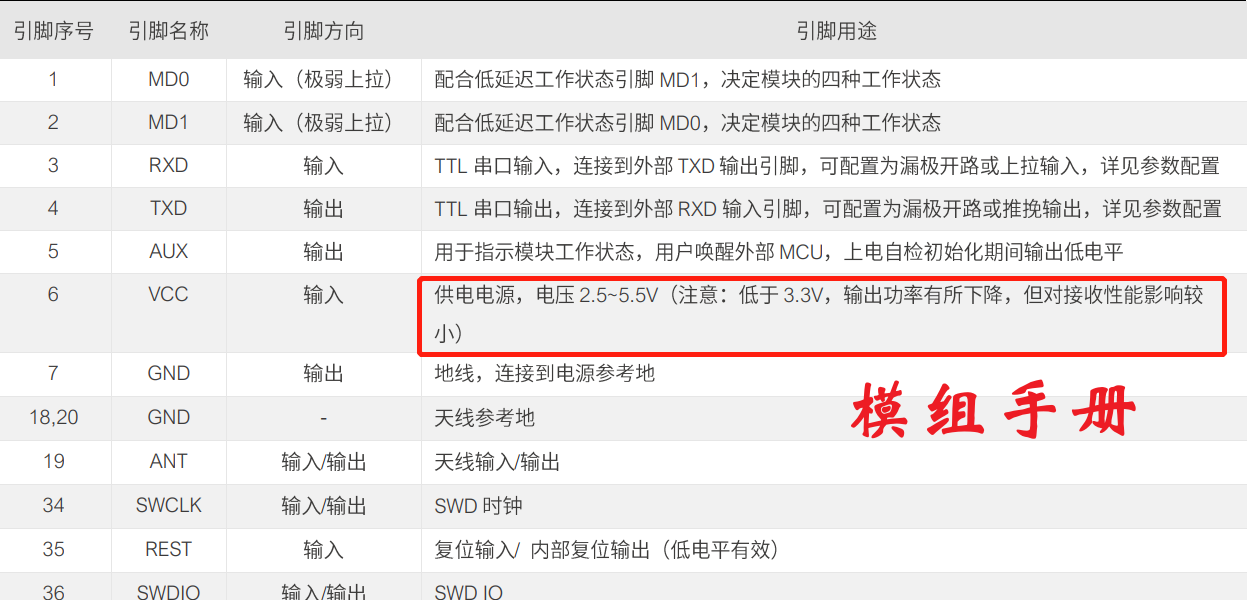
要解这道题目，感觉最关键的因素就是找到第  件任务最晚开始的时间 。这个看似简单，但是对建模的功底要求相当高。我一开始就把  当成了  ，但其实不是的。后者就相当于把第  件任务锁死在最后面完成，但其实是允许放在之前完成的，只要还满足截止日期即可，所以应当在  和当前的  之间选取一个较小值再减去  获得  才是转移过程中当选择第  个任务时的上一个状态。

#include<iostream>
#include<vector>
#include<algorithm>
#include<cmath>
using namespace std;

struct Node {
    int p, l, d;
};

int main() {
    int n;
    cin >> n;
    vector<Node> arr(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> arr[i].p >> arr[i].l >> arr[i].d;
    }
    sort(arr.begin(), arr.end(), [](const Node &a, const Node &b) {
        return a.d < b.d;
    });
    int t = arr.back().d;
    vector<vector<int>> dp(n + 1, vector<int>(t + 1));
    for (int i = 1; i <= n; i++) { // 第i件物品
        for (int j = 1; j <= t; j++) { // 前j天
            int k = min(arr[i].d, j) - arr[i].l; // 第i件任务最晚开始的时间
            dp[i][j] = dp[i - 1][j]; // 默认不选第i件
            if (k >= 0) {
                dp[i][j] = max(dp[i][j], dp[i - 1][k] + arr[i].p); // 注意体会这里k的含义，为什么不是j没有涵盖所有的情况
            }
        }
    }
    cout << dp[n][t] << endl;

    return 0;
}